Saludos queridos lectores, bienvenidos nuevamente. En esta oportunidad les presento una nueva serie de publicaciones, que denomine Introducción a las Ecuaciones Diferenciales Parciales (EDP), en la misma desarrollaremos este tan importante e interesante tema, en donde podemos aprender muchas aplicaciones, sobre todo en el campo de la física, química, biología y otras ciencias, así como no podemos dejar de mencionar sus aplicaciones a la ingeniería y carreras afines. Dentro de los problemas que se modelan con EDP podemos mencionar algunos: propagación del calor, propagación del sonido, dinámica de fluidos y muchos otros. La misma está dirigida al público en general (aunque debemos acotar, es un tema de un nivel más alto, para el que es necesario tener de algunos conocimientos previos de análisis real, ecuaciones diferenciales ordinarias, geometría diferencial, entre otros), con atención especial a profesionales y estudiantes universitarios en ciencias, ingeniería y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

---

---

Introducción

El objetivo que persigo con escribir esta serie que denomine Introducción a la Ecuaciones Diferenciales Parciales, es hablar un poco de este fascinante tema de las matemáticas, como los son las ecuaciones diferenciales parciales, donde presentaremos el aspecto teórico, junto con las aplicaciones a algunos problemas de ciencias físicas e ingeniería. Para el lector que quiera aprender acerca de este tópico, es necesario que cuente con una formación matemática rigurosa, ya que algunas de las demostraciones o explicaciones las obviaremos con el fin de avanzar en las aplicaciones. Durante esta serie de publicaciones desarrollaremos los métodos de solución de problemas que involucran EDP en su formulación.

Por nombrar algunos de los conocimientos previos debemos mencionar: un curso de Cálculo Avanzado, donde se hace un extenso estudios de las funciones de varias variables, un curso de Ecuaciones Diferenciales Ordinarias (los interesados pueden leer la serie de Ecuaciones Diferenciales Ordinarias de mi autoría), conocer un poco de probabilidades para el estudio de algunas aplicaciones estocásticas, entre muchos otros, que iremos nombrando a medida que vayamos avanzando en el tema.

---

---

Introducción a las de Ecuaciones Cuasilineales y Lineales de Primer Orden

Consideremos una función incógnita de, al menos, dos variables. Una ecuación que consista de esta función y algunas de sus derivadas parciales es lo que se llama una Ecuación Diferencial Parcial, o por sus siglas, EDP. Algunas de las notaciones que usaremos de ahora en adelante serán:

• Si
  
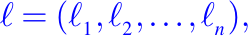
  es un vector cuyas componentes
  
  
  son todas números enteros positivos, entonces está recibe el nombre de multi-índice de orden
  
  
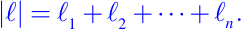
• Si dado un multi-índice entonces se define
  
  
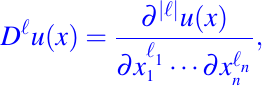
  otra forma de expresar lo anterior es usando la notación
  
  
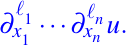
• Si k es un entero no negativo, se define D^ku(x) como el conjunto de todas las derivadas parciales
  
  tales que
  
  es decir, el conjunto de todas las derivadas parciales de orden k. Así,
  
  
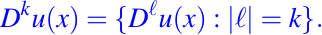
• El módulo de D^ku(x) se define como
  
  
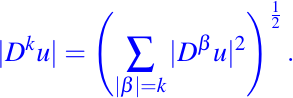
• Si k=1, se tiene
  
  
  lo cual es el gradiente de u y, usualmente, se denota por
  
  
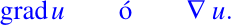
• Si k=2, se tiene
  
  
  la cual se le conoce como la matriz Hessiana.
• El Laplaciano de u, muy conocido en EDP's, se define como
  
  
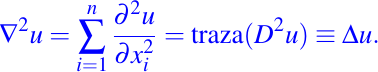
• Algunas veces usamos subíndices con los símbolos para denotar las variables que se están diferenciando. Por ejemplo, si
  
  
  entonces:
  
  

Una vez vistas algunas de las notaciones que usaremos, vamos a definir una EDP, como sigue:

Observación: Al resolver una EDP, es necesario encontrar todas las funciones u(x) que satisfagan la ecuación (1), ahora bien, cuando nos referimos a encontrar las soluciones lo que queremos decir, es que debemos obtener soluciones simples y explícitas, o, en caso contrario, deducir la existencia y otras propiedades de las soluciones.

Una pregunta natural, es preguntarse: ¿qué es una solución? La respuesta a esa pregunta está en la siguiente definición:

Ahora bien, debemos de clasificar las EDP's de 1er orden, dicha clasificación la haremos según la forma que tenga la función F.

1. La ecuación diferencial parcial dada en (1) se llama lineal si está se puede escribir de la forma general como:
   
   
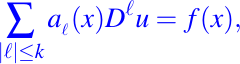
   donde f(x) y a_l son funciones dadas, cuando f(x) es idénticamente cero, la ecuación se llama homogénea. Por ejemplo, la ecuación de la forma
   
   
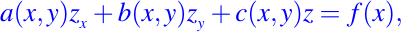
   es una ecuación lineal. Como podemos apreciar, la la función F de la definición de EDP, es lineal en z_x z_y y z y los coeficientes dependen de las variables independientes x e y solamente. Un caso particular, una EDP escrita de la forma siguiente:
   
   
   es una EDP lineal.
2. La ecuación diferencial parcial dada en (1) se llama semilineal si se puede escribir de la forma general como:
   
   
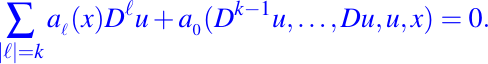
   Por ejemplo, la ecuación de la forma
   
   
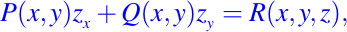
   es una ecuación semilineal, notemos que los coeficientes de z_x z_y son funciones que depende solamente de las variables independientes. Un caso particular, una EDP escrita de la forma siguiente:
   
   
   es una EDP semilineal.
3. La ecuación diferencial parcial dada en (1) se llama cuasilineal si se puede escribir de la forma general como:
   
   
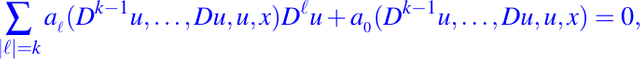
   por ejemplo, la ecuación de la forma
   
   
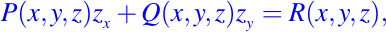
   es una ecuación cuasilineal, notemos que la función F de la definición de la EDP's es una función lineal en las derivadas y los coeficientes de P(x,y,z), Q(x,y,z) y R(x,y,z) son funciones que depende solamente de las variables independientes x, y con la variable desconocida z. Un caso particular, una EDP escrita de la forma siguiente:
   
   
   es una EDP cuasilineal.

---

---

Curvas Integrales y Campos Vectoriales

Uno de los principales puntos antes de empezar a estudiar EDP's, es conocer los métodos para hallar curvas y superficies integrales de campos vectoriales. Además de ser importantes por la gran gama de aplicaciones en diferentes áreas de las matemáticas, física e ingeniería.

Definamos un campo vectorial, como sigue: Sea

un campo vectorial definido en un subconjunto


Entonces, para nuestro desarrollo solo consideraremos campos vectoriales que cumplan con las siguientes condiciones:

1. El campo vectorial no sea idénticamente cero, es decir,
   
   
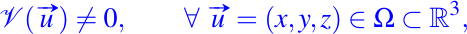
   en otras palabras, las funciones componentes P(x,y,z), Q(x,y,z) y R(x,y,z) no se anulan de manera simultanea en cada punto de Omega.
2. Las funciones componentes P(x,y,z), Q(x,y,z) y R(x,y,z) sean de clase C¹, es decir, que por lo menos sean continuamente diferenciable una vez.

Veamos algunos ejemplos de campos vectoriales:

• Sea el campo vectorial descrito por:
  
  
  como podemos apreciar, este satisface las dos condiciones en cualquier subconjunto de R³, incluso si tomamos a el mismo.
• Sea el campo vectorial descrito por:
  
  
  este campo vectorial satisface las dos condiciones en todo el espacio, menos en el origen de coordenadas, por lo tanto el subjunto donde definiremos este campo vectorial es:
  
  
• Sea el campo vectorial siguiente:
  
  
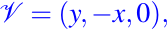
  este satisface las dos condiciones sobre todo el espacio, excepto en el eje z.

Una vez, definido lo que es un campo vectorial, nos faltaría definir a una curva integral, la cual la definiremos de la forma siguiente:

Muy bien, es de hacer notar, que en el campo de la física, una curva integral de un campo vectorial a menudo ea llamada una línea de campo. Si el campo vectorial es un campo de fuerza, las curvas integrales se les conoce como líneas de fuerza. Por ejemplo, si tenemos la influencia de un campo de fuerza ejercido por un imán, si colocamos limaduras de hierro alrededor, estas se agruparan a lo largo de las líneas de la fuerza del imán.

Ahora si el campo vectorial, es un campo de velocidad del flujo de un fluido, las curvas integrales de se le denominan líneas de flujo, y estos son los caminos de movimiento de las partículas de fluido.

Entonces, para hallar curvas integrales de los campos vectoriales, debemos entonces hacer que la tangente a la curva integral sea igual al campo vectorial, es decir,

Vamos a describir el procedimiento para hallar dichas curvas integrales, para ello debemos recordar que la tangente a un curva, viene dado por:

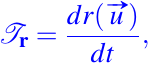
así, usando la ecuación anterior a esta, podemos entonces formar el siguiente sistema de ecuaciones:


de esta manera si resolvemos el sistema de ecuaciones dado en (2), estaríamos encontrando las curvas integrales asociadas al campo vectorial dado.

La manera de resolver el sistema dado en (2), es eliminando la dependencia sobre la variable t, lo cual podemos realizar ya que P(x,y,z), Q(x,y,z) y R(x,y,z) son independientes de la variable t.

Por lo tanto, si P(x,y,z) es distinto de cero, entonces tenemos:

Si Q(x,y,z) es distinto de cero, entonces tenemos:


Si R(x,y,z) es distinto de cero, entonces tenemos:


Luego los sistemas de ecuaciones dados en (3), (4) y (5) se pueden reescribir equivalentemente en la forma siguiente:


de allí deducimos que sus soluciones son superficies. Podemos entonces decir, que las curvas integrales de un campo vectorial se pueden considerar como las intersecciones de tales superficies.

---

Por ejemplo, describamos los sistemas de ecuaciones de los campos vectoriales que ya hemos vistos.

1. El sistema de ecuaciones asociados al campo vectorial de nuestro primer ejemplo es:
   
   
2. El sistema de ecuaciones asociados al campo vectorial de nuestro segundo ejemplo es:
   
   
3. El sistema de ecuaciones asociados al campo vectorial de nuestro tercer ejemplo es:
   
   

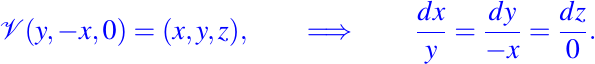
Los ceros que aparecen en los denominadores no deberían de molestarnos, ni alarmarnos, pues si tomamos el tercer ejemplo, esto significa

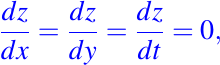
y por lo tanto una curva que sea solución de este ejemplo, debe estar en cualquier plano z=constante. Como lo podemos observar en la figura siguiente:


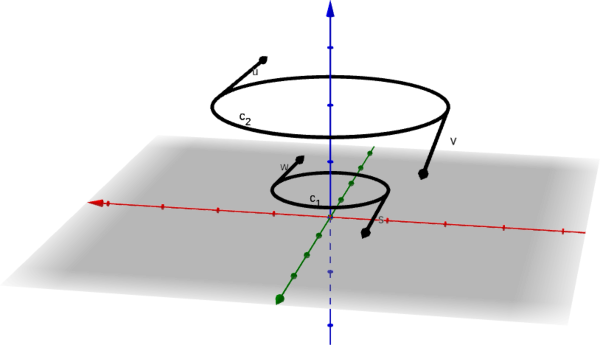
_{Imagen elaborado con GeoGebra, por @abdulmath.}

---

---

Queridos amigos y lectores, espero hayan disfrutado y aprendido en esta primera entrega de la serie de Introducción a las Ecuaciones Diferenciales Parciales, de igual manera los invito para la próxima entrega de esta serie, donde continuaremos tratando este tema tan interesante y de mucha aplicación. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

• Lang, Serge. Calculus of Several Variables. Springer Science & Business Media, 2012.
• Edwards, Charles Henry. Advanced Calculus of Several Variables. Courier Corporation, 2012.
• Dennemeyer, Rene. Introduction to Partial Differential Equations and Boundary Value Problems. 1968.
• Pinchover, Yehuda, and Jacob Rubinstein. An Introduction to Partial Differential Equations. Cambridge University Press, 2005.

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por abdulmath usando software libre, , GIMP e Inskcape.

_{Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.}