Differential Calculus: Time Rates
Hi steemians!. Today I'll be sharing my knowledge about differential calculus, specifically time rates.
Times rates can be solved by differentiating. It's a worded problem in differential calculus. One variable is given/solved with respect to time.

The problem above is an example of a time rates problem. We'll answer that as we go beyond in this discussion.
My way of solving the problem above is...
✔Read and analyze the problem.
We should know what is being asked, what are the given values and when to use it.
✔Assign variables for easy manipulation.
In the problem, our variables are..

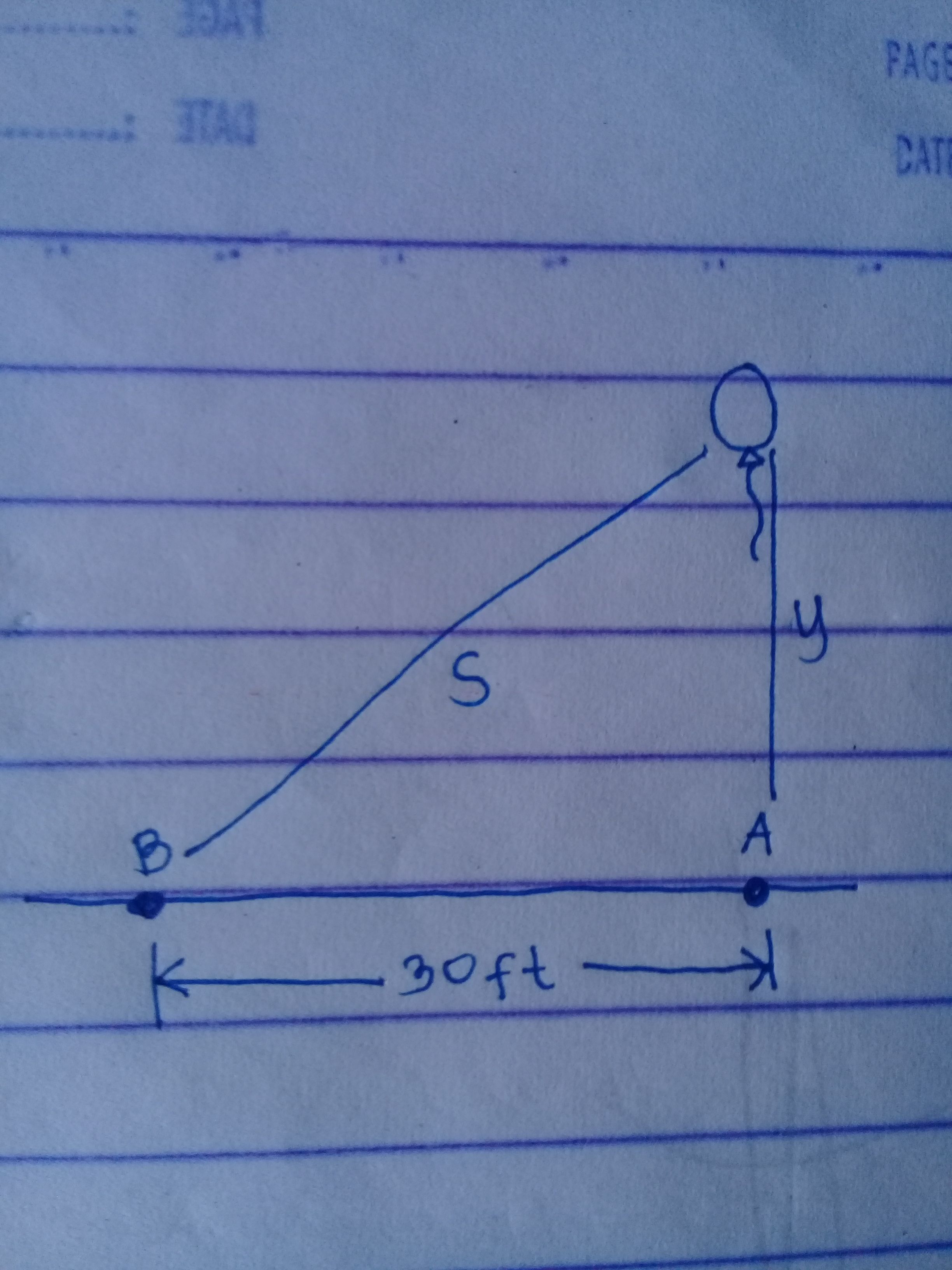
✔Draw a figure if necessary.
Based on the problem, the figure is..
✔Formulate equations.
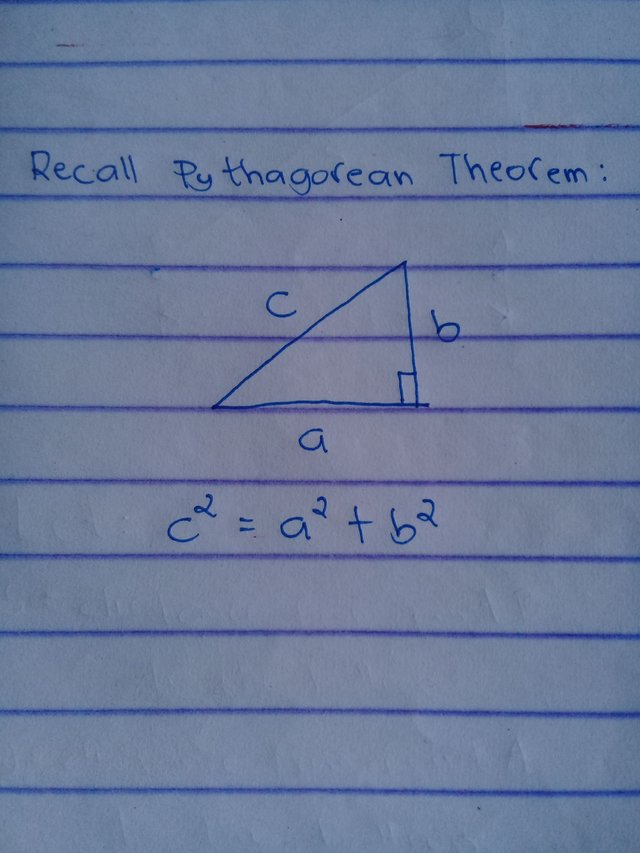
Based on the figure above, we can conclude that points A, B and the balloon forms a right triangle so we can use pythagorean theorem.
So..
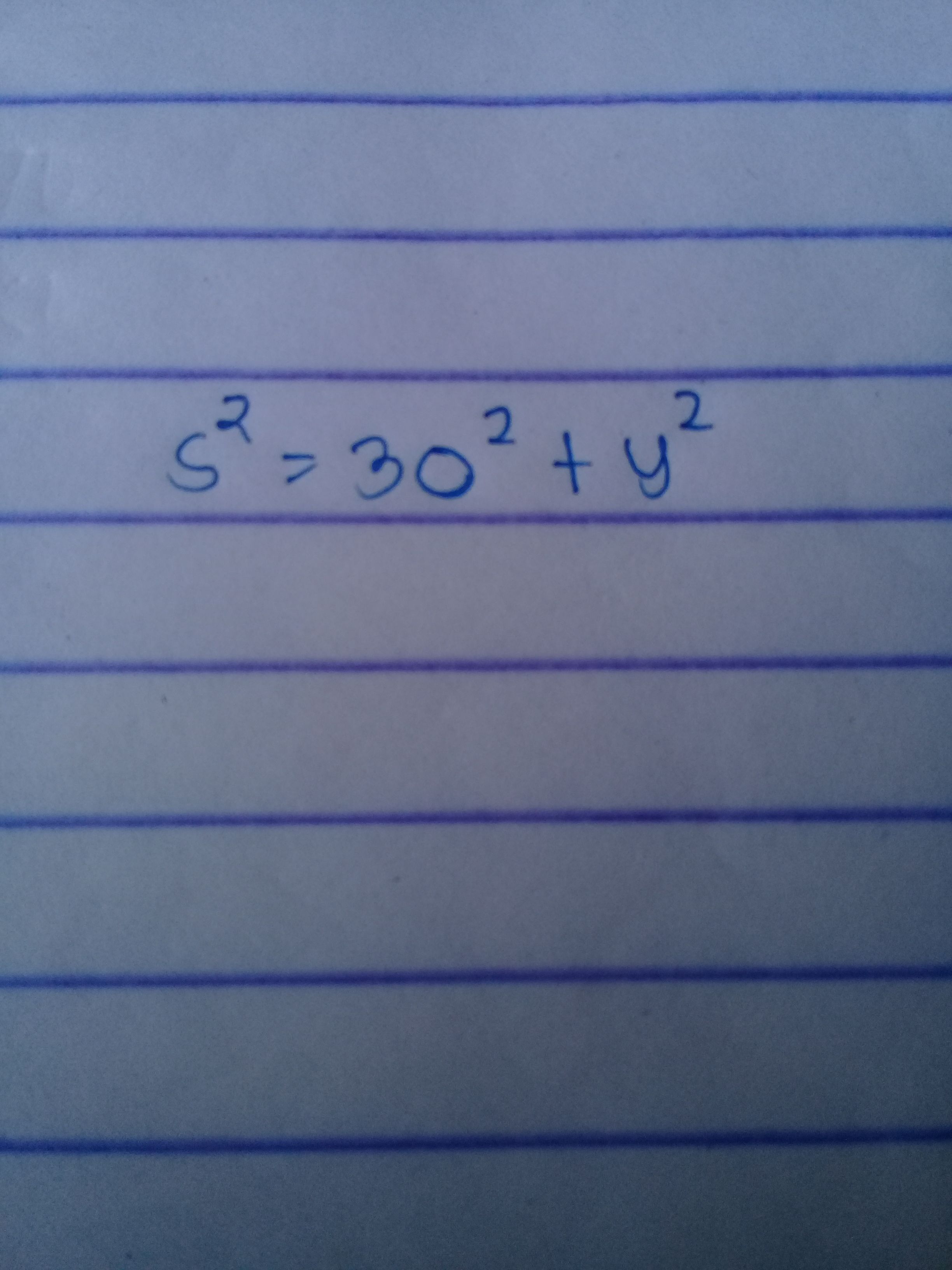
That is our equation.
✔Differentiate.
Since the value being asked is the rate of change of distance from the balloon to point B, we have to differentiate the equation above.
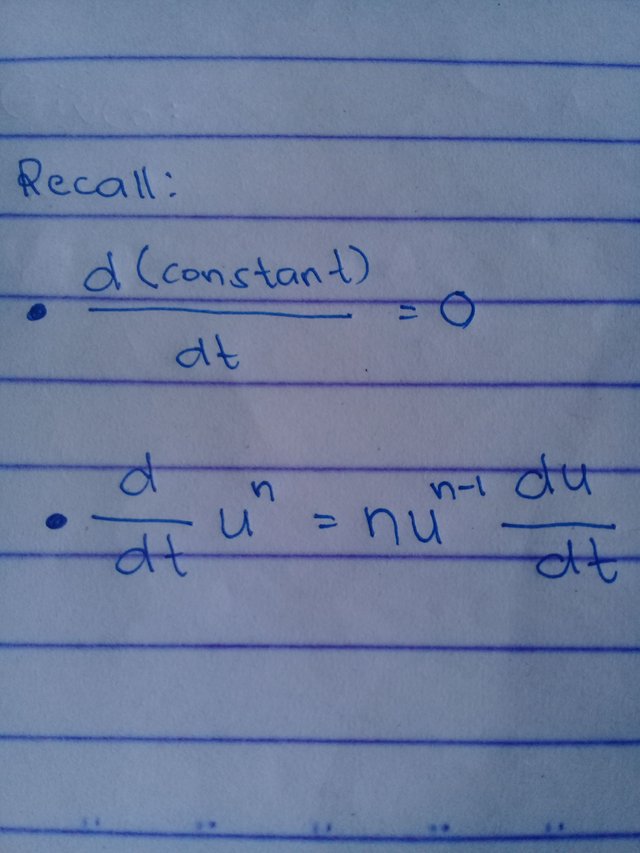
So..
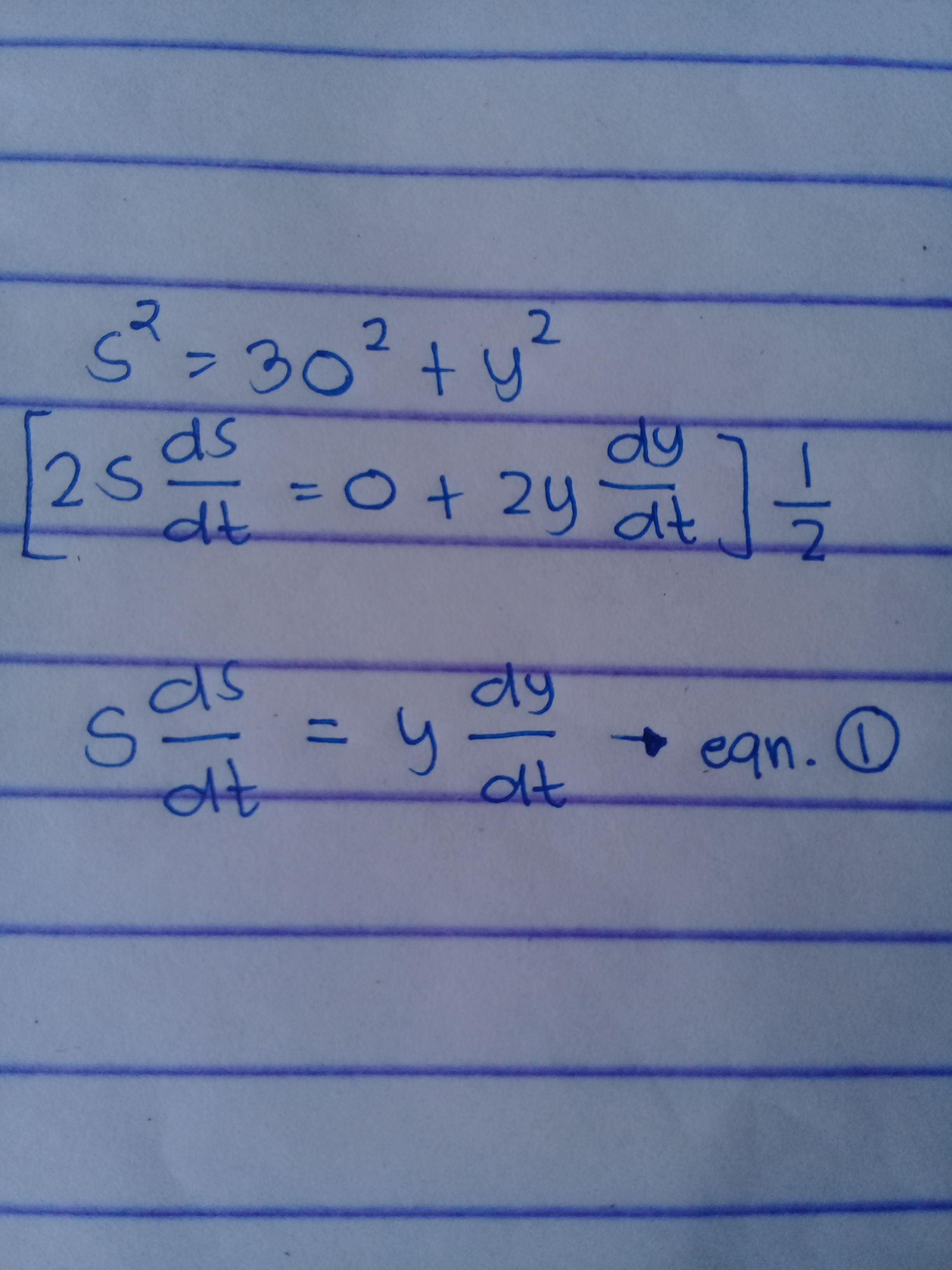
Equation 1 is our true equation. The equation above is the equation needed to get the final answer.
✔Complete the values needed.
We already have the value of y which is 40ft and the value of dy/dt which is 15ft/s. Now, we have to find the value of S when y is equal to 40.
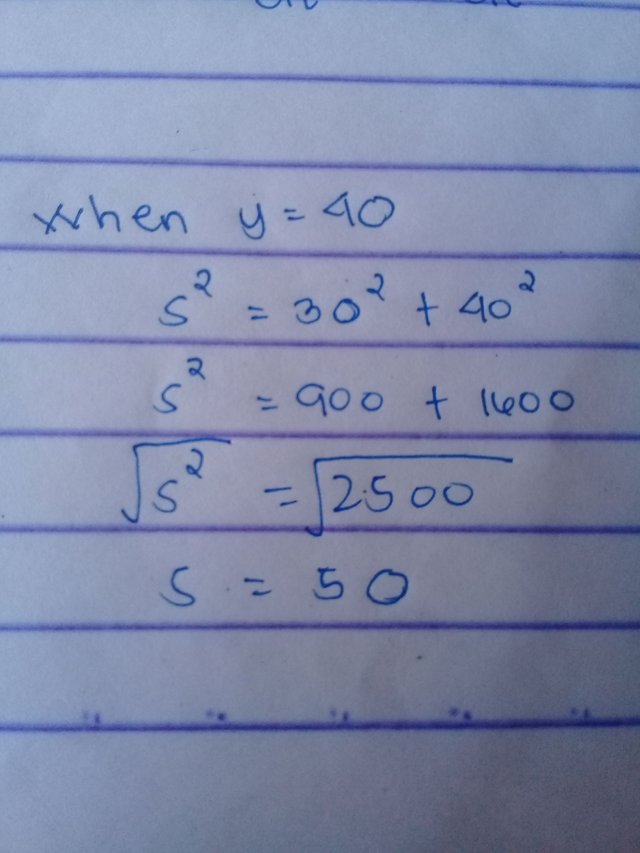
Now, all values needed to answer the problem are complete.
The values are..
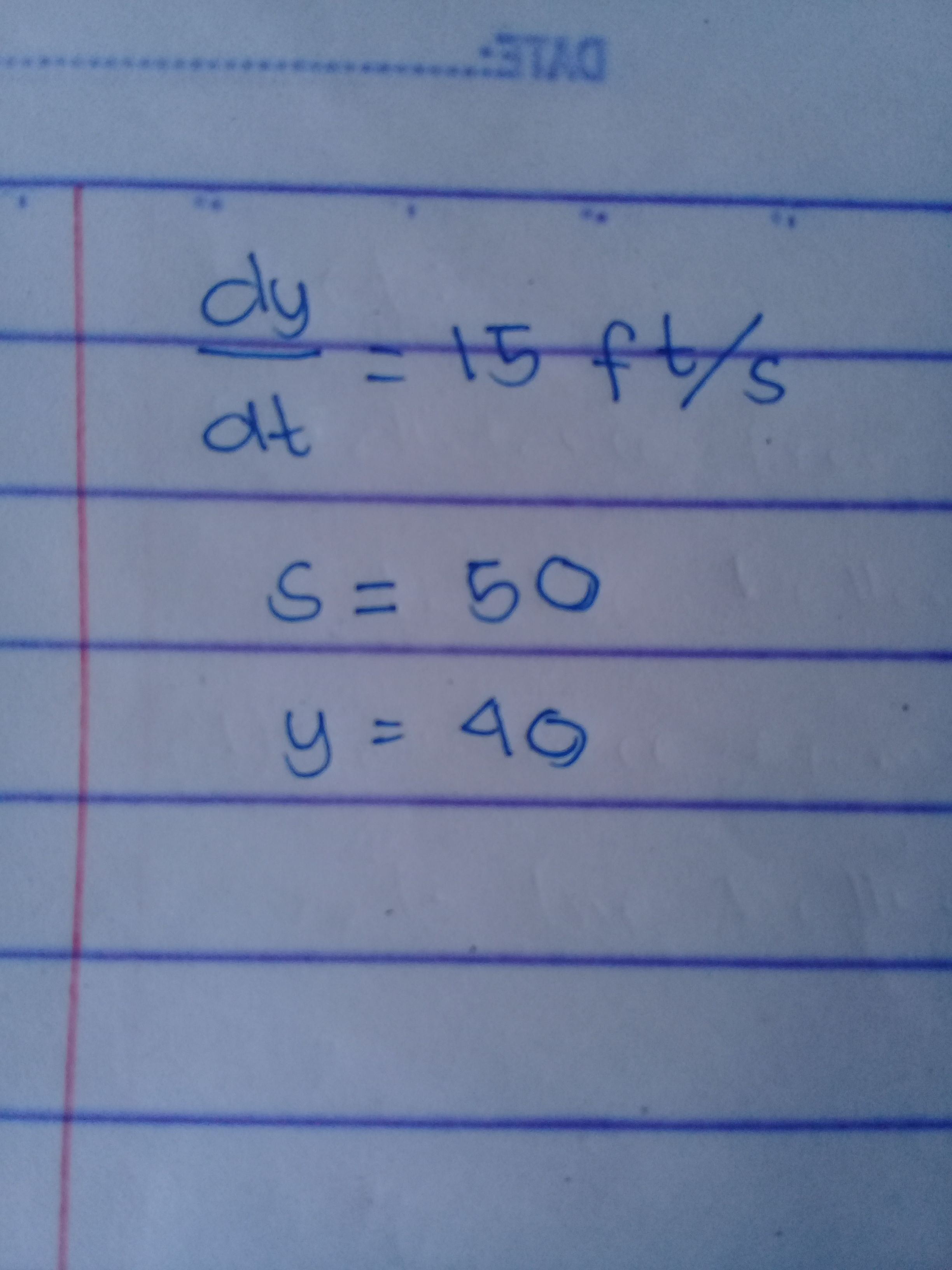
Note: dy/dt is the rate of change of distance from point A to the balloon.
✔Substitution and manipulation.
Now, lets find the answer.
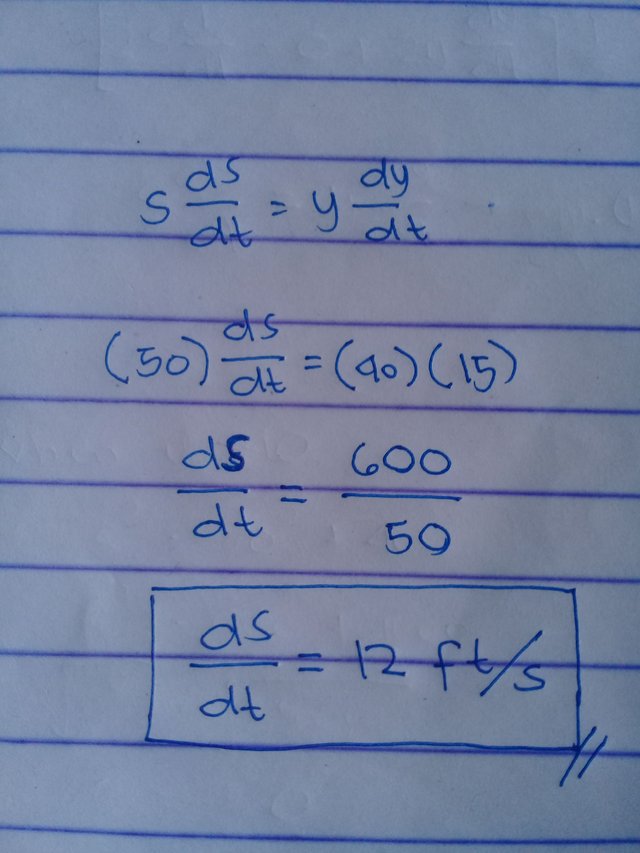
12ft/s is our final answer.
I hope you learn something. Enjoy the day and Have a great day guys! God Bless!
100% upvote you get 0.29 by @shakilbd. Thanks you.
Thank you so much :D
Agay! Wa koy nasabtan.
LR!
toink! math!!!! labad ulo nako kabayan! hahaha!
Wahahahaha :D salamat sa upvote diay :D
always man jud na basta bisdak full support jud ko! hahaha!
Salamat kaayo :D