Why to study Complex Number?
Natural numbers are used in everyday life. But, complex number system is not used in daily life. So, there may not be enough motivation for students to study this chapter. Complex number system has great importance in the field of mathematical physics. Also, a lot of real world technology and applications are based on complex analysis. So, it is of mere importance to have good knowledge about complex number.
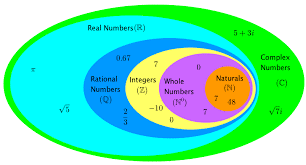
First we defined natural numbers as set of counting numbers.
When arithmetic operations were operated on natural numbers, the result wasn't one of the natural numbers. eg. a- b, when b > a, so we extended mathematics to integer number system.
When two natural numbers are divided, it always didn't include integer so, mathematics was extended to rational number.
Then, equation of form a x^2 = b, came and mathematics was extended to irrational number and finally to real number system.
This is called real number system but its not more real than complex number system in any way.
Let us try to solve the following polynomial equation. x^2 +3 = 0. It follows x^2 = −3 ”
The square of the positive number is a positive number and square of the negative number is also a positive.”
How can square of the number be a negative number?? If we plot y = x^2 +3, this curve does not intersect x-axis. So, there is no any real value of x satisfying this equation. If we try to solve algebraically, x = √−3 In secondary school, we left this type of solution as solution doesn't exist. But, we can write this in a mathematical form if we define, i = √−1. i here is called iota. It was first used by Leonard Euler, one of the pioneers of mathematics.
x = √−3 = √3∗−1 = √3i
Here using complex number we extended the mathematics.
Consider a real axis, denoted by infinite horizontal line. What does 5 + 4 mean? It simply means go five steps in forward direction and again go 4 steps forward. What does 5-4 mean? It means go 5 steps forwards and 4 steps in negative (backward) direction. So, negative number denoted the negative i.e. backward direction. Let us draw a Cartesian plane i.e. x-y plane. When we say 1 + i= 1+1i, we can visualize in x-y plane. It means go 1 step ahead in x axis again 1 step ahead in x axis and rotate later line segment by +90 degrees. The final point gives the point which is representation of complex number. If, we get i we rotate in - 90 degree. (Here, x is called real axis, y is called imaginary axis and plane is called complex plane or Argand plane.) Consider a problem;
√−1∗√−1 =?
Simply √−1∗√−1 = √−1∗−1 = √1 = 1?
No, because for √a√b = √ab ; a and b should be non-negative numbers. If we use idea of complex number; √−1√−1 = i∗i = i^2 = −1 ; by definition. Complex number enabled us to find as many roots as we want. For the given n degree polynomial equation, we can now find n roots. So, if
x^1000 = 1, then we can find 1000 roots of 1. In higher mathematics using complex analysis we can even find i^th root of i. Isn't that fascinating? Along with abstract, there are lots of practical applications. Complex numbers are generally encountered in physics and mathematics. It has many applications but I will list some of those which I have personally used.
In Solving Differential equation
In quantum mechanics, wave function is a complex.
In electrical engineering, Impedance of capacitor and inductor is expressed in terms of complex number.
Wave equation is complex.
Using Euler's identity, we can unite complex number, trigonometric functions, exponential and logarithmic functions.
Computation of real integral using residue theorem. So, its really important to learn about complex numbers.
At last,
That’s not only magic it does. We can find cube root, 999^th root, π^th root even i^th root. Whatever complex root we chose and whatever complex number we apply it to.
I remember doing a lot on complex numbers in high school, but never to the point where we were told any real-world applications... do you know what physicysts or engineers use them for every day? I don't know much about these fields but I can't imagine wave functions help us build bridges?
There was some weird way of expressing complex numbers which had a real compnent... like sin(x)+icos(x)? or some such... good old days!
I'm just starting out but feel free to check out my page here too! Havn't posted much STEM yet but there will be more to come :)
Well, I am into mechanical engineering. So, I have some idea about the applications. In control system, we use complex analysis to know about the stability of any system. In bridge, when the vibration becomes equal to natural frequency, it oscillates with large displacement due to which it may collapse. We may get an idea of the frequency of vibration using complex numbers(FFT, Fast Fourier Transform; Fourier transformation uses complex functions.). Generally while solving problems in the paper, it leads us to an equation containing differential called differential equation. For certain type of diff equations, complex analysis is needed to solve them. Probably, you may have heard about quantum mechanics. In it, the wave function is complex. It is the fundamental physical parameter to approximate various possibilities. Probably, there may not directly use of complex number in daily life. But, it is important especially in deeper research.
The one you talking about is euler relation which connects exponential function with trigonometric using complex number.
e^ix = cos x + isin x
Ah, I've seen the resonant frequency of bridges come up a few times in engineering videos! It's awesome that it does have such an important function!
Haha yeah that's the only. It's been so long!
Thanks heaps for the explination!
never thought about complex numbers this way.....thanks for sharing @bikkichhantyal.....
Welcome. I will be posting about STEM. Followed.