Vector Field and Scalar Field

Hello steemians, hope you had the great day. Today, with this post, I want to commence series of posts about vector calculus. In this part, I will describe vector field and scalar field in brief.

1.1 Vectors and Scalars

Before going directly into fields, at first, I want to give a brief introduction to vectors and scalars. Physical phenomena are described mathematically by physical quantities. These quantities may need magnitude only or magnitude and direction both for their specification. On the basis of that, quantities are divided into two groups.

1.1.1 Scalar:

If the physical quantity needs the only magnitude to completely specify it then it is called scalar. eg. mass, temperature, energy, speed etc.

1.1.2 Vector:

If the physical quantity needs both magnitude and direction to completely specify it then it is called vector. eg. electric field, weight, velocity, momentum etc.

1.2 Scalar Fields

Scalar field associates every point in a space with a scalar value.

y = f(x) is the common functional notation. Here, x is independent and y is the dependent variable. The value of y at different x is given by this equation.

y = x^2 is an example. It is the one dimensional scalar field.
In three dimensional scalar field, w = f(x,y,z)

Here, the value of functional value of w at coordinate (x,y,z) is given by function f(x,y,z). Let's integrate this concept with physical quantity.

Consider two dimensional temperature field as T(x,y) = 25 - x^2 - y^2

In the plot, the temperature is plotted in the z-direction and it is also shown by the color distribution.

Then,
The value of temperature at (0,0) = 25
The value of temperature at (1,1) = 23
The value of temperature at (1,2) = 20
The value of temperature at (0,1) = 24
The value of temperature at (0,5) = 0

The temperature field can be plotted in Matlab. I plotted the surface and the result is following;
Screenshot (120) (1).jpg

some of the examples of scalar fields are pressure fields in fluid, temperature field in physical space etc.

1.3 Vector Fields

Vector field associates every point on space with the vector. So, the value has both magnitude and direction. For the force field, both the magnitude and direction of the force is specified by the point in space. We can visualize the force field as series of arrows where the length of arrows denotes magnitudes and the point of the arrow shows direction. The force being vector can be resolved into components.

F = F_x(x,y,z) i + F_y(x,y,z) j + F_z(x,y,z) k

Here, F_x, F_y, F_z are scalars.

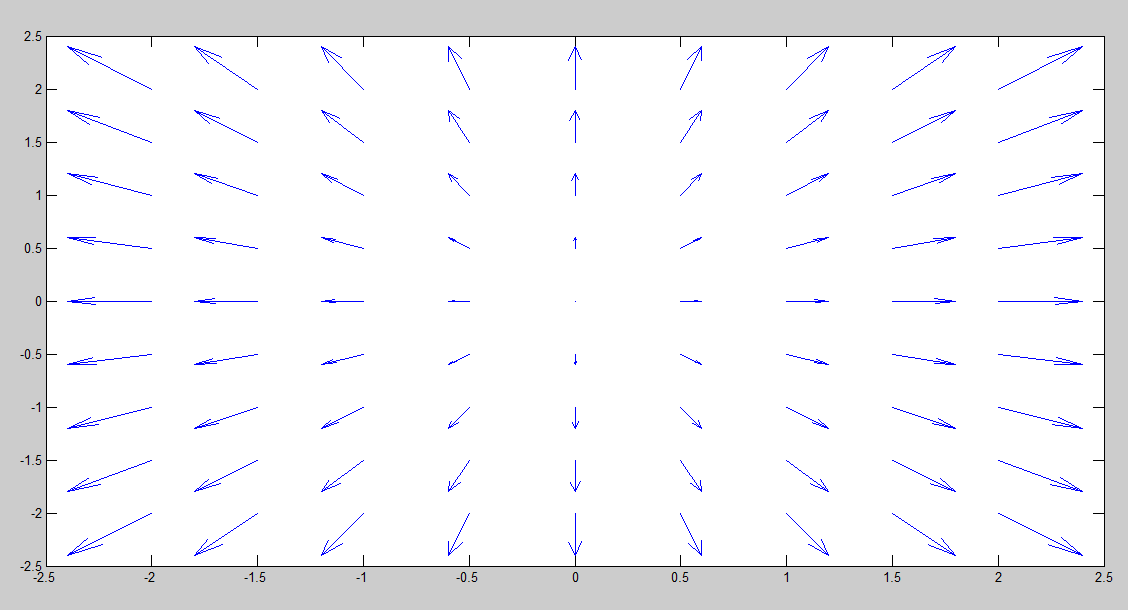
Let the force field in two dimensions be:

F = x i + y j

At point (1,1), magnitude = √ 2 and direction 45 degree with horizontal.
At point (-1,1), magnitude = √ 2 and direction 135 degree with horizontal.
At point (-1,-1), magnitude = √ 2 and direction 225 degree with horizontal.
At point (1,-1), magnitude = √ 2 and direction 315 degree with horizontal.

At point (2,2), magnitude = √ 8 and direction 45 degree with horizontal.
At point (-2,2), magnitude = √ 8 and direction 135 degree with horizontal.
At point (-2,-2), magnitude = √ 8 and direction 225 degree with horizontal.
At point (2,-2), magnitude = √ 8 and direction 315 degree with horizontal.

The plot in the Matlab is the following:

Sources

Thomas Calculus

Div Grad Curl and All that