You are viewing a single comment's thread from:
RE: Steemit's Got Issues! Community Discussion - Whales Cannot Decide Everything - Take 1
Honestly, I am not much caring about curation. For me, upvotes are a tool to promote discussions, help friends and reward good work.
I set most of my auto votes to first minute to decline curation myself and the cost of it is minimal.
Like this post had multiple big bots on it, but I still voted, effectively forfeiting my curation.
A N log(N) curve with selectable amount of curation rewards would be great. That could fix many issues.
That’s right, there should be more experimentation with different reward curves to find what works best. Anything but linear would be better in my opinion.
Well, I officially do not know what a N log(N) curv is lol. I'd love to know more!
When I vote a post I really never even think of the curation. It really only helps you if you have a lot of sp.
I am thankful for those with considerable sp that are not driven by the curation reward incentive. It's a shame that they are not more common. :)
I'm definitely interested in knowing what the n log(N) fix you speak of is.
As this discussion grows I believe I will be able to not use bots to get it noticed :)
There is
N
N log N
N * N (or N^2)
Basically a middle ground.
I'll take your word for it... lol
middle ground makes sense :)
Check this:
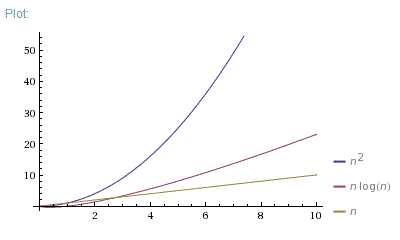
Maybe that makes more sense :)
Ok, so it is basically a curve that will somewhat limit reward pool payout while keeping an acceptably stable growth curve compared to what is now just kinda paying out like crazy and depleting the pool quicker? While also keeping the payout desirable, if I'm seeing this right.
Let me know how close I'm getting. lol
Actually, I guess I should have asked which one we are using now so I knew what I was looking at here.
So steemit.com is cutting off the graph, but basically:
If n is the number of Steem Power you vote with (simplified), then say you have 100 and someone else has 1000.
N:
100 = 100.
1000 = 1000.
N log N (with log base 10)
100 * log(100) = 100 * 2 = 200
1000 * log(1000) = 1000 * 3 = 3000
N^2 = N* N:
100 * 100 = 10000
1000 * 1000 = 1000000
So a n^2 curve favors the rich, an n curve favors everyone, n log n favors the rich, but not by much.