El Interesante Mundo de los Cuerpos Geométricos. Part. #2
Hola, apreciados miembros de la comunidad científica de #CERVANTES, #STEM-EspanoL, #SteemSTEM, y STEEMIT en general, bienvenido nuevamente a mi blog. La presente publicación es continuación del tema de cuerpos geométricos; donde la publicación anterior se describió los Poliedros Regulares, en esta le daremos continuidad a los poliedros irregulares y posteriormente estaré publicando los cuerpos redondos
Video 1. Presentación del Post. Poliedros Irregulares. Edición: @xeliram.

El propósito de esta publicación es satisfacer las necesidades de profesores y estudiantes en el sentido de disponer de un material didáctico, ya que se presentan ejemplos, problemas resueltos y actividades propuestas. Espero que sea de total agrado a la comunidad #STEM-Espanol y a cualquier persona que le sirva de apoyo a su labor educativa.
ÍNDICE
- Poliedros Irregulares
2.1 Prisma
2.2 Prisma oblicuo
2.3 Pirámides recta
2.4 Pirámide inclinada

Los poliedros Irregulares son poliedros cuyas caras son polígonos no todos iguales. Hay infinidad de poliedros irregulares. Se dividen en los siguientes tipos: Prisma y Pirámides.
2.1 El Prisma
Se denomina prisma, al poliedro comprendido entre dos poliedros iguales y paralelos, que reciben el nombre de bases, las demás caras son paralelogramos.
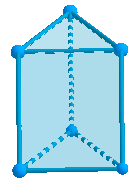
Los polígonos ABC y DEF reciben el nombre de bases del prisma.
ABFD, BCEF, ACED son las caras del prisma (paralelogramo) o caras laterales, están son las caras que no son base.
Las arista que no pertenecen a la base se llaman aristas laterales
La altura es la distancia entre los planos de las bases.
Los prisma pueden ser recto u oblicuos, según que sus aristas sean o no, perpendicular a los planos de las bases.
Es un prisma recto cuando sus aristas laterales son perpendiculares a los planos de las bases. El prima anterior es recto. En este caso, la altura coincide con las aristas laterales.
Es un prisma oblicuo cuando sus aristas laterales no son perpendiculares a los planos de las bases. En este caso la altura es la perpendicular traza desde una base a la otra o a su prolongación.
Dependiendo del número de lados de los polígonos que forman las bases, los primas se clasifican en: Triangulares, cuadrangulares, pentagonales, hexagonales, entre otros.
Prisma Triangular: Tiene de base un triángulo.
Prisma Cuadrangular: Las bases son cuadrilátero.
Prisma Pentagonal: Las bases son pentágonos.
Prisma hexagonal: Las bases son hexágonos.
Paralelepípedo
Se llama paralelepípedo al prisma cuyas bases son paralelogramos. Las caras opuestas son iguales y paralelas.
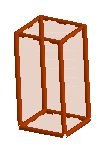
El paralelepípedo de base cuadrada y lados formados por rectángulo, recibe también el nombre de prisma cuadrangular recto.
El paralelepípedo de base cuadrada y lados iguales y perpendiculares a los de la base es llamado hexaedro o cubo.
El paralelepípedo de base rectangular, recibe el nombre de ortoedro.
Diagrama y construcción.
Siguiendo las instrucciones y materiales para construir poliedros descrita en la publicación: Cuerpos geométricos realicemos el prisma cuadrangular recto y el ortoedro respectivamente:
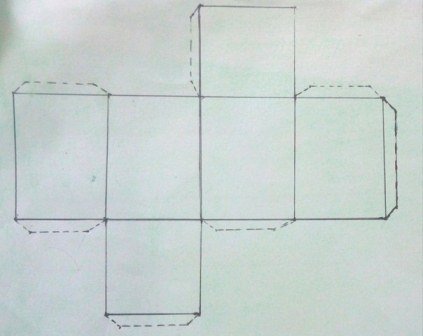
Fuente: Paralelepípedo Cuadrangular. Diseñado por la autora @xeliram foto tomada con un celular.
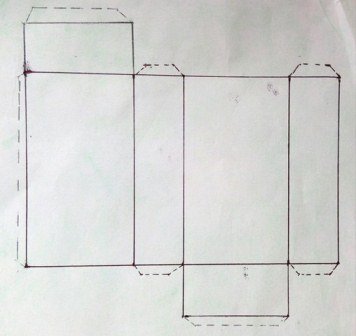
Fuente: Paralelepípedo Rectangular u Ortoedro. Diseñado por la autora @xeliram foto tomada con un celular.
En el siguiente gráfico, se observa como quedo las construcciones de los Paralelepípedo elaborado en cartulina.


Fuente: Construcciones de los Paralelepípedo. Diseñado por la autora @xeliram foto tomada con un celular y editada en la aplicación FotoCollage
El paralelepípedo de base cuadrada su área se calcula de la siguiente manera:
El área de la base: es el área del cuadrado que las forma.
El área lateral: es igual al perímetro de su base por la altura.
Siendo P = Perímetro y a = Altura
Su área total es la suma del área lateral más el área de las dos bases.
Siendo Al=área lateral y B=área de la base
Su volumen es igual al área de la base por la altura.
Siendo B=área de la base y a = Altura
Un paralelepípedo formado por seis rombos iguales es un romboedro o paralelepípedo oblicuo, es decir que el romboedro es un prisma oblicuo.
Un paralelepípedo de base en Romboide, es un prisma oblicuo cuyas bases y lados son paralelogramos romboides iguales dos a dos. Los romboides son los paralelogramos que no son ni cuadrados, ni rectángulos, ni rombos.
Por lo que los paralelepípedos oblicuos podemos encontrar a los romboedros y romboides
Prisma Pentagonal Regular
Es un poliedro irregular, ya que sus caras no son todas iguales. Está formado por dos pentágonos iguales y paralelos que son las bases. Sus caras laterales son rectángulos.
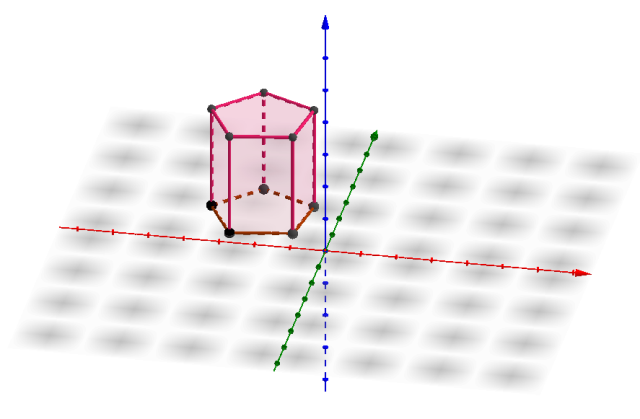
Fuente: Prisma Pentagonal. Exportada del Geogebra como vista gráfica a imagen. Elaborada por @xeliram
El área de la base, será igual a la mitad del producto del perímetro por su apotema, dado que la base está formada por un pentágono.
Siendo P = Perímetro y ap = apotema
El área lateral de un prisma es igual al perímetro de la base por la altura.
Siendo Al = área lateral, P = perímetro y a = altura
El área total, es la suma del área lateral y el área de ambas base.
Siendo At = área total, Al = área lateral y B = área de la base
En el siguiente vídeo les muestro como realizar un Prisma Pentagonal con el Geogebra.
Video 2. Prisma Pentagonal. Edición: @xeliram.
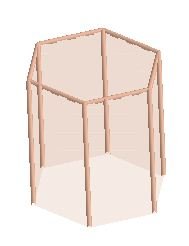
Prisma Hexagonal Regular
Es un poliedro irregular cuyas bases son dos hexágonos iguales y sus caras laterales, rectángulos.
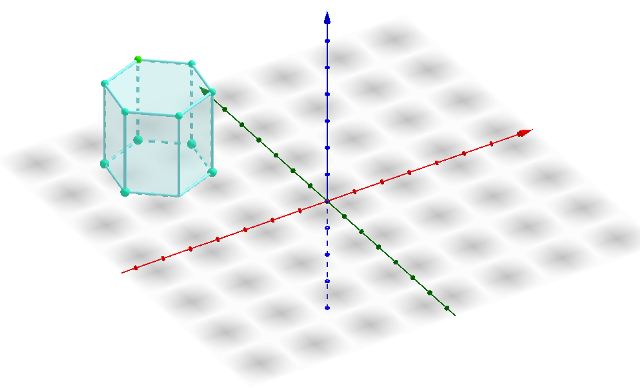
Fuente: Prisma Hexagonal. Exportada del Geogebra como vista gráfica a imagen. Elaborada por @xeliram
Área de un Prisma
Al desarrollar un prisma recto de lado l y altura a cuya base es un polígono regular de n lados, apotema ap y lado l se obtiene:
- Un rectángulo de base igual al perímetro P de la base y altura a.
- Dos polígonos regulares correspondientes a las bases del prisma.
Veamos el siguiente ejemplo
Calcular el área lateral y total de un prisma recto de altura 4cm y base hexagonal de lado igual a 1cm y apotema de 0.87cm
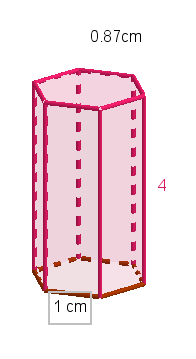
Fuente: Ejemplo 1. Diseñado por la autora @xeliram. Realizada en Geogebra.
ACTIVIDAD 1
El área total del prisma de la figura es y el área de su base es
. Determinar la altura del prisma.
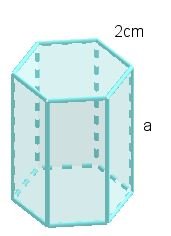
Fuente: Actividad 1. Diseñado por la autora @xeliram. Realizada en Geogebra.
2.2 Pirámide
La pirámide es un cuerpo geométrico que tiene por base un polígono cualquiera y sus caras laterales son triángulo que se juntan en un punto común, llamado vértice de la pirámide.
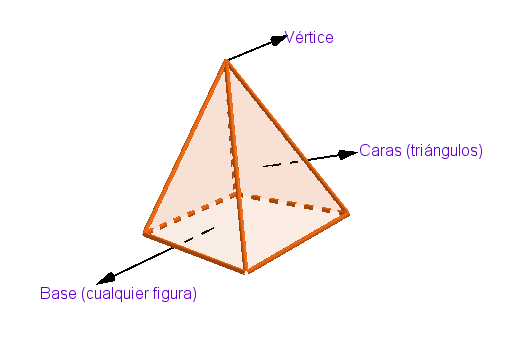
Fuente: Elementos de la Pirámides. Diseñado por la autora @xeliram. Realizada en Geogebra.
Dependiendo del polígono que forme la base, las pirámides se clasifican en triangular (la base es un triángulo), cuadrangular (la base es un cuadrilátero), pentagonal (la base es un pentágono), hexagonal (la base es un hexágono), etc. Si es de base triangular tiene 3 caras, si es de base cuadrada tiene cuatro cara, así sucesivamente. Las pirámides tienen tantos triángulos en las caras laterales como lados tiene la base.
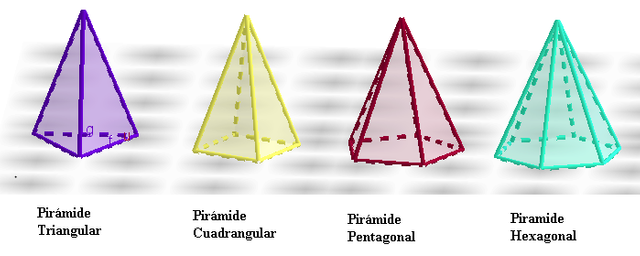
Fuente: Tipos de Pirámides. Diseñado por la autora @xeliram. Realizada en Geogebra y editado en Paint.
Las pirámides según la inclinación de su eje puede ser pirámide regular o recta y pirámide oblicua.
Pirámide Regular es aquella cuya base está formada por un polígono regular y su altura coincide con el centro de la base. En una pirámide regular las caras laterales son triángulos isósceles y la altura de cada uno de estos triángulos recibe el nombre de apotema de la pirámide.
El área lateral de una pirámide es la suma de las áreas de las caras laterales. El área total de una pirámide es la suma del área lateral y del área de la base.
Fuente: Matemáticas Galdós
El área lateral (Al) de un pirámide es igual a la mitad del producto del perímetro (P) de su base por la apotema (ap) de la pirámide (altura de los triángulos laterales).
En efecto:
Para hallar el área lateral de una pirámide, extendemos sobre un plano las caras laterales.
El área lateral se obtendrá multiplicando el área de uno de los triángulos de las caras laterales por el número de caras laterales (n), así pues,
Sea l = lado de la base y ap = la apotema de la pirámide, el área de una cara será:
Pero como n×l=perímetro=P, tenemos: Al=(P×ap)/2
Por lo tanto área total:
At=Al+B donde At=área total, Al=área lateral y B=área de la base
Pirámide Oblicua
Se dice que una pirámide es oblicua cuando no todos los triángulos laterales son isósceles y la línea que une el vértice de la pirámide y el centro de la base cae inclinada hacia la base.
ACTIVIDAD 2
Completa el siguiente cuadro:
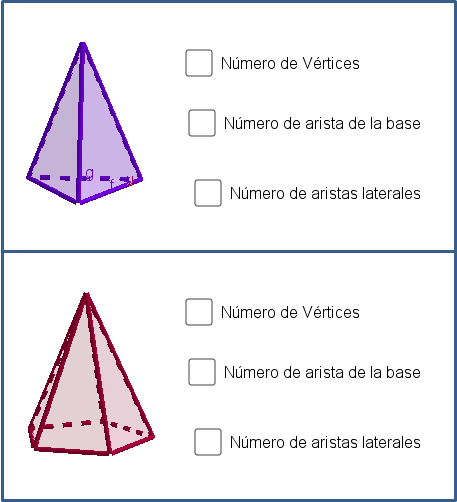
Fuente: Actividad 2. Diseñado por la autora @xeliram. Realizada en Geogebra y editado en PowerPoint.

- Los prismas tienen dos bases y caras que son paralelogramos; mientras que las pirámides tienen una base y sus caras son triángulos isósceles y se unen en un punto llamado vértice de la pirámide.
- Todas las civilizaciones antiguas han construido pirámides.
- Los panales de abejas tienen forma de un prisma hexagonal

- Hinds, J. (2002). Matemática de 7mo. Editorial PREMIER. Venezuela, caracas.
- 18 cuerpos geométricos para armar. Ediciones CO-BO Caracas.
- Matemáticas Galdós (2004). Madrid España.
- Pirámides. Disponible: http://www.bartolomecossio.com/MATEMATICAS/pirmides.html
Nota: Los títulos fueron creadas y editadas por @xeliram usando Powert point
Si estás interesado en contenidos sobre Ciencia, Tecnología, Ingeniería y Matemática, consulta las etiquetas #STEM-Espanol y #SteemSTEM, las cuales puedes utilizar para publicar contenidos en estas áreas. @SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad.
Soy Marilex Porteles profesora de Matemática, investigadora, soñadora, me gusta tejer, nadar y soy madre de una hermosa niña.
Dale UPVOTE si te gusto, COMENTA y RESTEEM para que otros se enteren GRACIAS

Dale UPVOTE si te gusto, COMENTA y RESTEEM para que otros se enteren GRACIAS


This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @utopian-io.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness and utopian-io witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Please consider setting @steemstem as a beneficiary to your post to get a stronger support.
Please consider using the steemstem.io app to get a stronger support.
Hi @xeliram!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Hola! @xeliram excelente el uso de Geogebra para el estudio de los cuerpos geométricos, es bueno estimular el uso de estos recursos para facilitar la enseñanza de la matemática. Otro programa excelente para la creación de figuras 3D es Google SketchUp, aunque no es una herramienta matemática sino de diseño su uso es sencillo y puede ser utilizado para muchas cosas. Saludos!
Gracias por tu comentario. El software Geogebra es bastante completo
Repollo es un proyecto que tiene como misión entregar recompensas a todos los creadores de contenido. Tú puedes recibir un voto de Repollo siempre si decides adquirir una membresía delegando desde 50 SP. @cervantes apoya a Repollo, Puedes votar por ellos como Witness aquí. No te olvides de seguir promocionando tus publicaciones en nuestro Discord.
gracias por el apoyo @beberepollo
Buen post, @xeliram! Te invito a usar https://www.steemstem.io la aplicación oficial de nuestra comunidad para esta blockchain.
Gracias por tu comentario e invitación. @eniolw
Muy bonito e ilustrativo tu post @xeliram, conceptos básicos sobre la matemática muy bien explicados, fabulosas imagenes!
Gracias @anaestrada12 por tu comentario