Vectores

solmar (54)in #spanish • 5 years ago

En el trabajo que frecuentemente se lleva a acabo en física se emplean cantidades que tienen propiedades numéricas e incluso direccionales. En este sentido, en física, se hace necesario tener presente la definición de vectores, pues las cantidades que además de su parte numérica se ven acompañadas por información de dirección reciben el nombre de cantidades vectoriales. Les invito, entonces, a que me acompañen a que estudiemos los vectores.

link

Introducción

En la presente publicación se dedicará especial atención a lo relativo a las cantidades escalares y vectoriales Se definen los vectores equivalentes y se analiza la adición y la resta de las cantidades vectoriales, junto con alguna aplicaciones comunes a las situaciones físicas.

Magnitudes escalares y magnitudes vectoriales

Muchas magnitudes físicas tales como el área, longitud, y masa, quedan completamente descritas dando un número real que representa la magnitud de la cantidad en cuestión. Tales magnitudes reciben el nombre de magnitudes escalares.

Sin embargo, otras magnitudes físicas no quedan completamente determinadas hasta que se especifica, además del número, su dirección. Estas magnitudes que además de un número se acompañan con dirección reciben el nombre de vectores. Este tipo de magnitudes, a nivel general, se denominan magnitudes escalares. Son ejemplo de magnitudes vectoriales, o simplemente vectores, la fuerza, el desplazamiento y la velocidad.

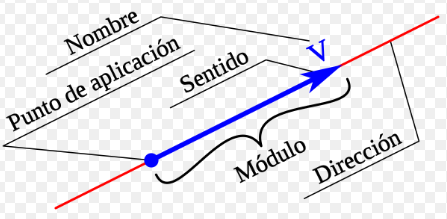
Los vectores se pueden representar mediante segmento de rectas dirigidas, o flechas, en el plano o en el espacio tridimensional. La dirección de la flecha especifica la dirección del vector y la longitud de la flecha determina su magnitud. La cola de la flecha se llama punto inicial del vector, y la punta de flecha recibe el nombre de punto terminal del vector.

link

vectores equivalentes

Se dice que dos, o más, son equivalentes, también llamados equipolentes, si tienen la misma longitud y la misma dirección. Dado que es conveniente que un vector quede completamente determinado por su longitud y dirección, los vectores equivalentes se consideran iguales aun cuando puedan tener posiciones diferentes. Si v y w son vectores equivalentes, entonces vamos a escribir:

v = w

Ejemplo:

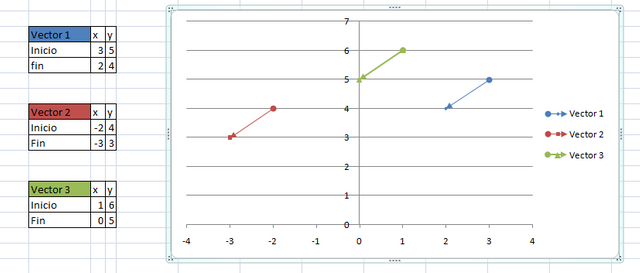
Nótese que los tres vectores, a pesar de tener ubicaciones distintas, tienen el mismo sentido, el mismo tamaño y son paralelos, lo que hace que los tres vectores sean considerados iguales, es decir, equipolentes.

Suma de vectores

Si v y w son dos vectores, entonces la suma de v + w es el vector que se determina de la siguiente manera. Coloque el vector w de tal manera que su punto inicial coincida con el punto terminal de v. Entonces, el vector v + w es el vector que está representado por la flecha que va del punto inicial de v al punto terminal de w.

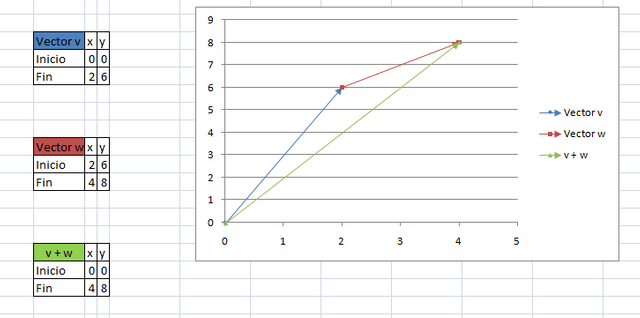
A nivel de práctica, puedes ver que la suma de vectores es conmutativa realizando la suma w + v notando que v + w = w + v, es decir, te resultará un vector suma equipolente al vector verde que se acaba de construir.

Resta de vectores

Si v y w son dos vectores, entonces la resta de dichos vectores se define como:

v - w = v + (-w)

Sin embargo, para obtener la diferencia de v - w sin tener que recurrir a el vector -w, se colocan los vectores v y w de tal manera que coincidan sus puntos iniciales; entonces, el vector que va del punto terminal de w al punto terminal de v es el vector v - w. Dicha situación la ilustramos en la siguiente imagen:

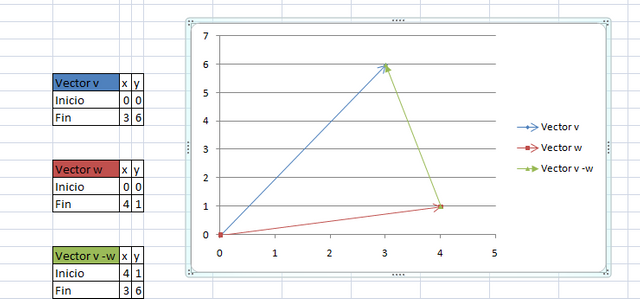
Hasta acá lo relativo al contenido inicial de vectores. Los invito a un próximo contenido cuando continuaremos abordando el maravilloso de la física ampliando la información de los vectores, les espero.