La teoría de conjunto debe su aparición, en el mundo de la matemática, a ilustres personajes como, sin duda, lo fueron Georg Cantor, Richard Dedekind y Gottlob Frege.

---

link

En un primer momento, lo relativo a la teoría de conjunto fue visto con cierta reservas, desconfianza y aversión dentro del ambiente matemático ya establecido, sin embargo, con el correr del tiempo la teoría de conjunto, por su considerable importancia en ramas de la matemática como la topología y la teoría de funciones, ha alcanzo un papel preponderante en el escenario de la Matemática Moderna resultando un absurdo, actualmente , hablar del desarrollo de las matemáticas sin considerar el aporte que se ha logrado desde la teoría de conjuntos.

En este contexto, en este primer post, respecto a la teoría de conjuntos, vamos a abordar lo relativo a la idea de conjunto y elementos, formas de determinar un conjunto, pertenencia y no pertenencia y la definición de conjuntos finitos y no-finitos. Iniciemos, acompáñenme!!

Elementos y conjunto

Al iniciar el estudio de la teoría de conjunto debemos hacerlo partiendo por dos ideas fundamentales, a saber, conjunto y elementos.

---

Ejemplos:

Las hojas de un cuaderno. los puntos de una recta, las rectas de un plano, los números naturales.

---

A su vez, cada uno de los objetos del conjunto es un elemento.

Los conjuntos los representamos con letras mayúsculas: A, B, C, …, etc., y a los elementos con letras minúsculas: a, b, c, …, etc.

Determinación de un conjunto

Los conjuntos, en matemática, los podemos determinar por extensión y por comprensión.

---

Ejemplos:

---

1.- El conjunto A cuyos elementos son 1, 3, 5 se representa así:

A={1,2.3}

2.- El conjunto B de los múltiplos de 5 se representa así:

B={múltiplos de 5}

---

En el ejemplo 1, el conjunto A está determinado por extensión, pues se han enumerado todos los elementos del conjunto. Por otro lado, en el ejemplo 2, el conjunto B está determinado por comprensión, pues se ha enunciado la propiedad que caracteriza sus elementos.

---

Pertenencia y no pertenencia

---

Ejemplos

---

La proposición:

“Venezuela (v) pertenece al conjunto de las naciones americanas (A)”, se representa así:

v ∈ A

---

Por otro lado, la proposición:

“Alemania (a) no pertenece al conjunto de las naciones americanas (A)”, se representa así:
a ∉ A

---

Conjuntos finitos y no-fintos

---

---

Ejemplos:

---

Los conjuntos:

---

---

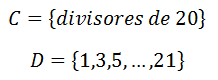
son conjuntos finitos, pues en cada caso sabemos cuales son todos sus elementos desde el primero hasta el último.

---

Por otro lado, los conjuntos:

---

N={0,1,2,3,4,…}

---

R={puntos de una recta}

---

D={polígonos del plano}

---

Son conjuntos no-finitos.

---

Hasta acá nuestro primer post, de dos que dedicaremos a la Teoría de Conjuntos, les invito a seguir acompañándome.