LAS ECUACIONES DIFERENCIALES PARTE 1: INTRODUCCIÓN
Como están amigos de steemit soy,
Como mencione en mi primer post soy estudiante de Física de La Universidad del Zulia (LUZ).
En esta oportunidad les quiero transmitir un poco de lo que he aprendido durante el curso de mi carrera.
Específicamente sobre las Ecuaciones Diferenciales (E.D).
Las ecuaciones diferenciales en si es un tema muy amplio. Yo me centrare en las aplicaciones a la física.
Las ecuaciones diferenciales son consideradas matemáticas avanzadas para ciencias e ingeniería.
Ejemplo:
La 2da ley de Newton, que es probable que la mayoría conozca y que comúnmente se enuncia como ''la fuerza es igual a la masa por la aceleración''. Es realmente una simplificación de una ecuación diferencial
![IMG_20171129_161530[1].jpg](https://steemitimages.com/DQmeJkQCnbiVkZ9YXWtPkdSSBKkTyNVg3spmSWh1yvvqC92/IMG_20171129_161530%5B1%5D.jpg)
De manera más general la 2da ley de Newton enuncia que la fuerza ejercida sobre un cuerpo es igual a la variación del momentum (cantidad de movimiento) con respecto al tiempo.
Donde momentum es igual al producto de la masa por la velocidad. Y se expresa como una ecuación diferencial
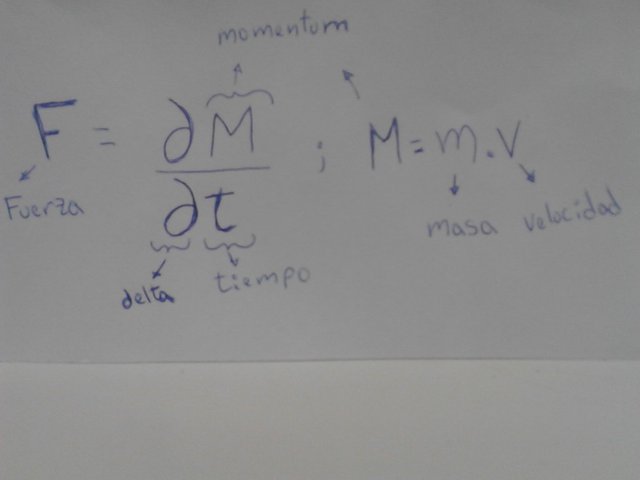
Que considerando la masa del cuerpo como constante. Encontramos que
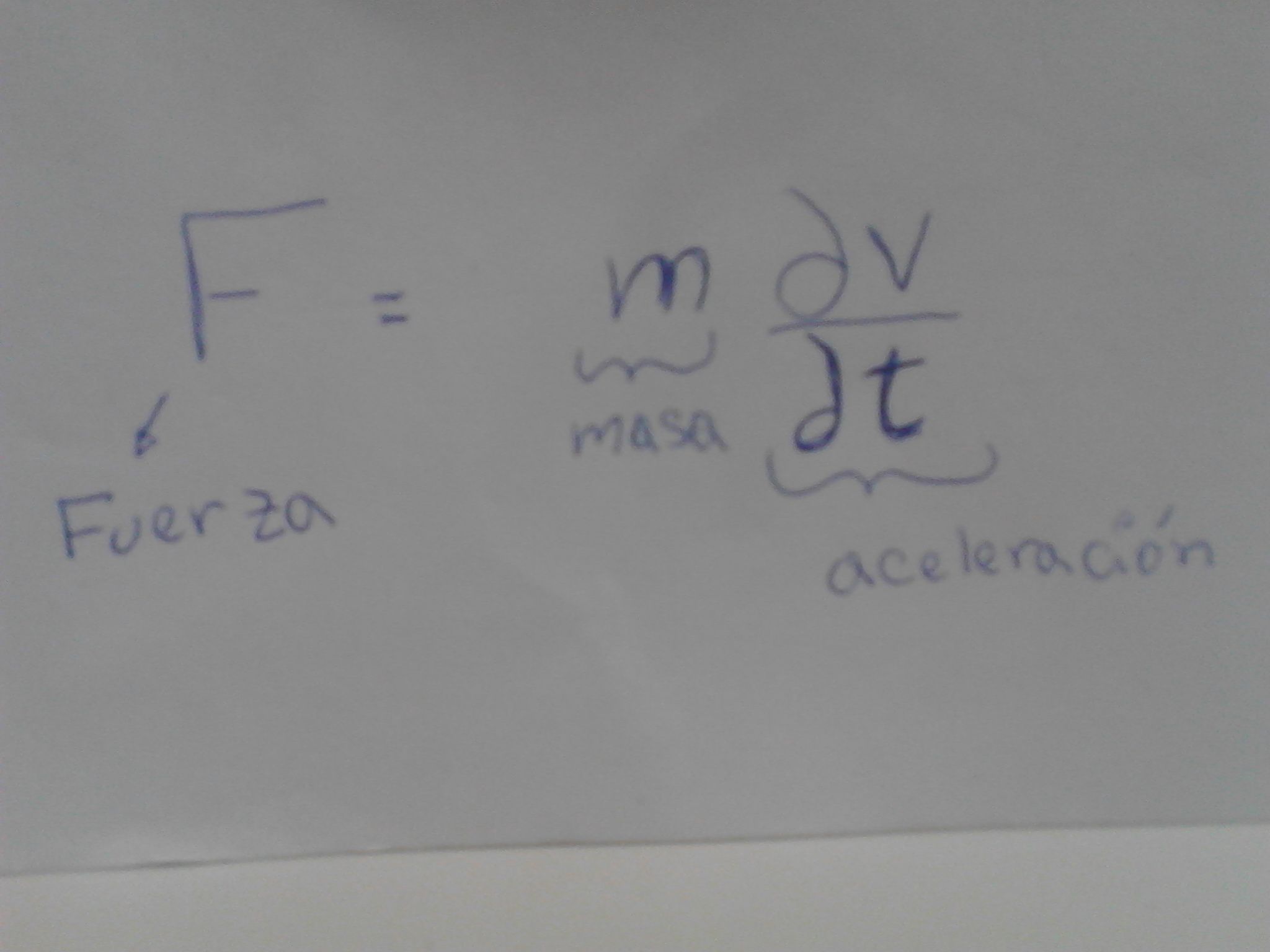
Ahora bien, conociendo lo importantes que son, vamos a definir que es una ecuación diferencial.
Matemáticamente: es una ecuación que relaciona una variable dependiente o función y las derivadas de esta con respecto a una o más variables independientes (son los parámetros que hacen variar la función).
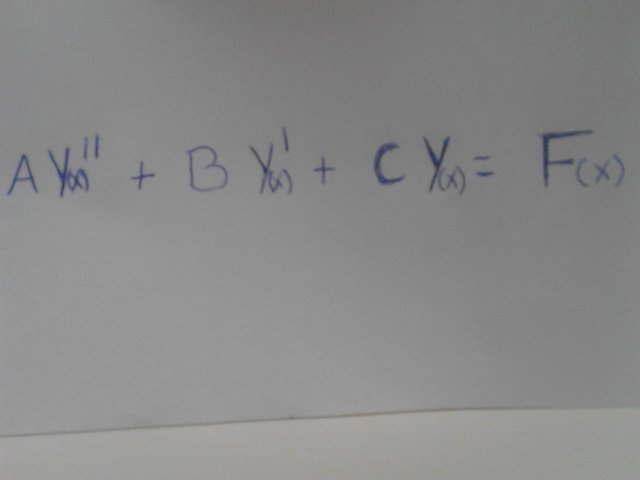
Físicamente: Se expresa como un modelo matemático que pretende reproducir o predecir el comportamiento de un sistema físico, con sistema físico me refiero a cualquier fenómeno de la naturaleza que queramos estudiar el movimiento de un cuerpo, la transferencia de calor, la conductividad eléctrica por nombrar algunos.
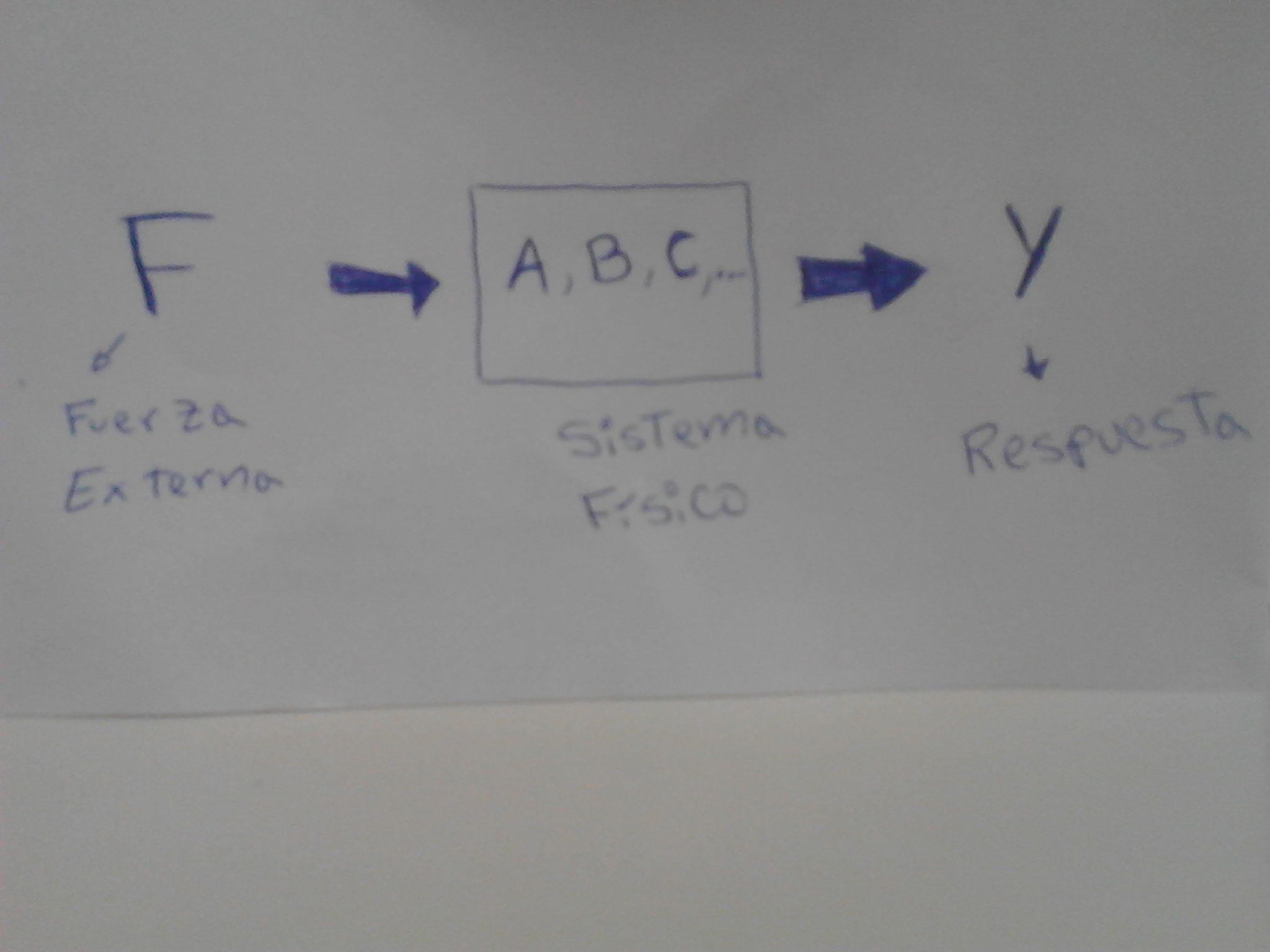
Por lo tanto si queremos estudiar algún fenómeno natural lo más conveniente será encontrar una ecuación diferencial que lo represente.
Yo como estudiante de física les muestro las aplicaciones en mi área de estudio pero la ecuaciones diferenciales son igual de útiles para estudiar problemas de otras ciencias como química, biología, economía, sociología, etc.
Habiendo definido lo que son: les mostrare la manera en que pueden clasificarse:
En las imagen 4 podemos ver las partes que conforman una ecuación diferencial y en la 5 lo que representa cada parte en la realidad de un sistema físico,
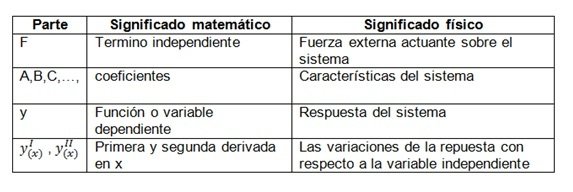
Entonces una ecuación diferencial tiene:
Orden: Es igual al de la derivada de mayor orden presente en la ecuación. (la que se muestra en la imagen 4 es de 2do orden).
Coeficientes constantes o variables: Depende de los valores de A, B, C y si estos son constantes o variables.
Grado: El grado de la ecuación diferencial será el grado de la derivada de mayor orden. La imagen 4 muestra una ecuación de grado 1 porque y^II(x) tiene potencia 1.
Lineal o no lineal: Si la ecuación tiene grado 1 y no existen productos entre la función y alguna de sus derivadas entonces esta se considera lineal de lo contrario esta será no lineal.
Ordinaria o parcial: si las derivadas involucradas en la ecuación son totales esta será ordinaria, si las derivadas son parciales la ecuación diferencial será parcial.
Homogénea o no homogénea: si el termino independiente F es cero la ecuación será homogénea si F es diferente de cero entonces la ecuación será no homogénea.
Las imágenes mostradas aquí mostradas fueron hechas por mí.
Hasta aquí llego con este post, con el que quería introducirlos en el tema, espero sea de su agrado.
Continuare con el tema en mis futuros post.
Referencias.
Kreyszig, E. 1985, Matemáticas avanzadas para ingeniería, 3ra edición, tomo I, editorial Limusa.
Boyce, W; Diprima, R. 2000, Ecuaciones diferenciales y problemas con valores en la frontera, 4ta edición, editorial Limusa.
Zill, D 1997, Ecuaciones diferenciales, con aplicaciones de modelado, 6ta edición editorial Thomson internacional.
Hola, como estas pidiendo sugerencias:
2)sumatoria de F=dp/dt (es la derivada total, no parcial)
Saludos
Muchas gracias profesora @emily61. Cierto es por convención se usa la p, y bueno sobre el tipo de derivada. Yo menciono que eso es antes de considerar la masa del cuerpo constante.
Soy nuevo en steemit! Este es mi 3 post. Así que cualquier sugerencia que me ayude a mejorar mis publicaciones sera bienvenida... gracias.