El problema de Sierpinski y las matemáticas de fractales.

Asistió a la escuela en Varsovia, donde su primer maestro de matemáticas descubrió pronto sus talentos para las matemáticas. Este fue el período de ocupación de Polonia, Rusia y tuvo un momento difícil para que el talentoso Sierpinski se educara en Polonia. Rusia impuso su lengua y cultura frente a los cambios implementados en todas las escuelas secundarias de Polonia entre 1869 y 1874.

El objetivo de Rusia era mantener la alfabetización más alta posible en Polonia, para que pudieran sentirse frustrados por el aprendizaje de los estudiantes.

A pesar de las dificultades, el Departamento de Matemáticas y Física Sierpinski ingresó en la Universidad de Varsovia en 1899. Cuanto más la universidad del emperador se convirtiera en una universidad de Rusia en 1869, el nombre oficial de la universidad se explicaría exactamente desde entonces. La universidad tuvo una conferencia enteramente rusa con personal en toda Rusia. Por lo tanto, no es sorprendente que sea el trabajo de un matemático ruso, un profesor de Voronoy, quien atrajo al primer momento a Sierpinski.

El Departamento de Matemáticas y Física de 1903 proporcionó el mejor premio para los ensayos de los estudiantes sobre la contribución de Voronoy a la teoría de los números . Sierpinski ganó una medalla de oro en la competencia por su tesis.

Recibió una medalla de oro de la Universidad por su trabajo en competencia para la teoría de los números. Fue mi primer trabajo científico (Dijo). Lo acepté para su publicación en la Universidad 'Izvestia' de Varsovia. Sin embargo, al año siguiente produje un boicot de escuelas polacas y rusas y no quería que mi primer trabajo se imprimiera en ruso, así que me retiré de la impresión. La huelga es la "Izvestiiya" de Varsovia.

En los años 50, Sierpinski se graduó de la Universidad de Varsovia y se fijó en el problema que tuvo una vez más con su grado de ocupación de la pole en Rusia:

Asistimos a una conferencia anual sobre el idioma ruso. ... el honor de cada alumno que el punto tiene el peor resultado sobre el tema. ... No respondí la pregunta que tenía ... y estoy insatisfecho Mark. ... Bueno, sugerí que repitiera el examen de instructor, de lo contrario aprobé todos mis exámenes para no obtener el título de candidato para ciencias matemáticas. ... (dijo) , la persona que aceptó los documentos para decir que el primer caso en nuestra universidad estaría en excelentes calificaciones en todas las materias y no obtendría el título de candidato para la medalla de oro, ciencia matemática, pero se negó a obtener un título inferior, El grado real del estudiante (extrañamente como se llamaba un grado más bajo) estaba en el idioma de Rusia debido a las puntuaciones más bajas.

Sierpinski tuvo la suerte de que alguien leyera las Escrituras, "bueno para su curso de idioma ruso", por lo que podría tomarse un tiempo para cambiar la marca. El dijo:

La policía era humana.

El resultado del documento de premiación dijo que Sierpinski fue un importante contribuyente al famoso problema en 1904 puntos de cuadrícula. Estudiemos (R) el número de punto (I, n) , que representa el radio r, que contiene el centro O en el círculo , I, A ~ Z. Hay una constante C y un número en K existe

| Investigación (R) - π r 2 | "CR es K.

Deje K menos vale la pena va a caer. Gauss 1837 Grupo D demostró una. La principal contribución de su Sierpinski D, 2 / 3 demostró que es posible mejorar la desigualdad. En 1913, Edmund Sierpinski Landau demostró resultados más cortos y profundos, siempre y cuando los probara. ya se hacia notar el joven matemático.

Ahora, discutamos sobre un trabajo adicional que hemos realizado en un tiempo y a lo que Sierpinski se refiere en este resultado es un "problema del círculo gaussiano". En 1923, mientras Van der Corput d es "2 / 3 demuestran que el 1915 Hardy Landau, d" 1 / 2 demostró. Al año siguiente Littlewood y la Walfisz d perro 163 / 247 y entonces se mejora y el Grupo D 37 / 56 demostraron. Vinogradov presentó una pequeña mejora en 1932 y Titchmarsh en 1934. Los mejores resultados [EFR] saben L 7 / 11.

Sierpinski se graduó en 1904 y al mismo tiempo trabajó como maestra de escuela en matemáticas y física en una escuela para niñas en Varsovia. Pero cuando la escuela cerró debido a la huelga, Sierpinski Krakóv decidió ir a estudiar su doctorado. En la Universidad Jagellónica, asistió a Krakóv, a matemáticas por Zaremba, también estudió astronomía y filosofía y enseñó. Recibió su doctorado y fue nombrado para la Universidad de Lvov en 1908.

De hecho, fue en 1907 cuando el primer conjunto se interesó por la teoría de Sierpinski. Apunta a un avión que podría especificarse como una de esas coordenadas, como lo afirmó a lo largo del teorema. Dijo que era posible que Banachiewicz, que se encontraba en ese momento en Gotinga, escribiera cómo preguntarle por estos resultados. Responde con una palabra que recibió 'Cantor'. Sierpinski y el conjunto de teorías En 1909 comenzó su primer estudio de las conferencias, que hizo todo lo posible para establecer la teoría completamente en el rumbo del enemigo.

A lo largo de su vida, Sierpinski ha mantenido una producción asombrosa de trabajos de investigación y libros. Durante el período de 1908 a 1914, enseñó en la universidad Lvov, publicó tres libros además de muchos trabajos de investigación. Estos libros son teorías de los números irracionales (1910), teorías de la teoría de la configuración de resumen (1912) y números (1912).

En 1960, Waclaw Sierpinski escribió que todos los enteros positivos nn, K 2 n + 1k2n+1Enteros positivos kkY el número de " Después de su nombre, un entero k impar.kSe llama el número de Sierpinski. La prueba de Sierpinski tiene una k específica.kEl valor de Selfridge no se presentó, pero dos años después, Selfridge fue k = 78557k=78557Logró demostrar la habilidad de esquiar pura pin. Echemos un vistazo más de cerca a sus pruebas.

Echemos un vistazo a uno de los cálculos anteriores. Si n ≡ 7( mod12 )n≡7(mod12)Si es apropiado, k ≥ 0k≥0Con respecto a n = 12 k + 7n=12k+7. Por lo tanto,

78557 ⋅ 2 12 k + 7 + 1 = 78557 ⋅ 8 4 k ⋅ 128 + 1 ≡ 3 ⋅ 1 ⋅ 2 + 1 ≡ 0

( mod7 )78557⋅212k+7+1=78557⋅84k⋅128+1≡3⋅1⋅2+1≡0(mod7)

Respectivamente. Los casos restantes pueden ser probados también.

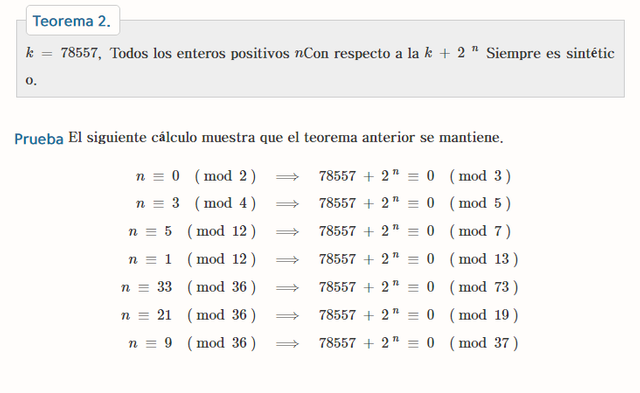
La prueba es 78557 ⋅ 2 n + 178557⋅2n+1Siempre es el siguiente set.

P = { 3 ,5 ,7 ,13 ,19 ,37 ,74 }

Se puede ver que uno de los elementos de? El conjunto pPSe llama un conjunto de cubierta. Es decir, el conjunto de portada es un subconjunto de números primos y todos los enteros positivos nnPara el k 2 n + 1k2n+1Esto siempre se establece PPY se divide en los elementos de. Se sabe que todos los números de Searfinsky conocidos hasta la fecha tienen un conjunto de portada.

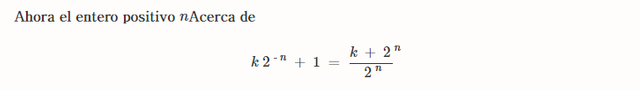
Todos los enteros positivos n & lt; RTI ID = 0.0 & gt;nCon respecto a la k + 2 nk+2nEl entero impar kkPuedes pensar en El kkSe llama el número dual de Sierpinski. Entonces, similar al teorema 1, k = 78557k=78557Puede resultar ser un número de pin doble cizalla.

Sabemos que hay infinitos números de Sierpinski debido a la prueba de Sierpinski, por lo que podemos pensar en el número más pequeño de Sierpinski. Sorprendentemente, sin embargo, el problema de encontrar el menor número de pastores sigue sin resolverse. Es decir, el número mínimo conocido de esquís de Shepherd hasta la fecha es k = 78557k=78557Sin embargo, el número más pequeño de Sierpinski sigue sin resolverse. Hasta ahora k = 78557k=78557Se juzgó que los cinco enteros impares más pequeños no eran el número de Searfinsky.

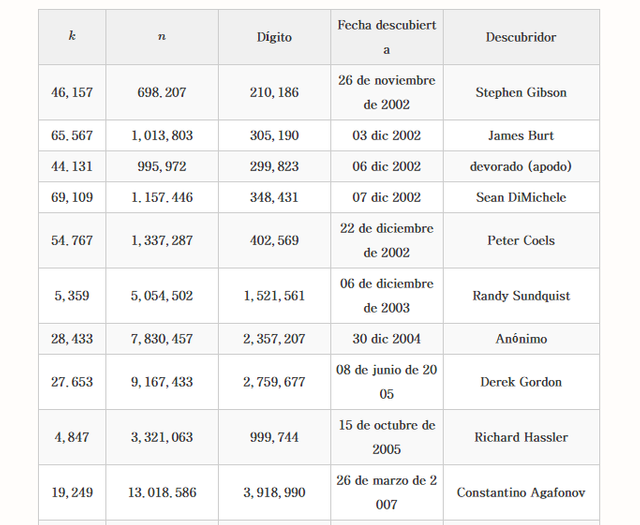
Dado un entero impar kkPara demostrar que no hay esquí de aleta pura, k 2 n + 1k2n+1Esto hace primo nnDebe existir. Pero la mayoría kkSi el valor es relativamente pequeño nnPara el k 2 n + 1k2n+1Pero en 2002 no se sabía si el número de pines de corte de enteros impares era 17. Desde entonces, se ha implementado un proyecto llamado "Seventeen o bust" para identificar los 17 montones de enteros impares que usan computación distribuida, y desde ese momento, desde enero de 2018, Se confirmó que todos los 12 números, excepto el número de perros, no eran Searfinsky.