Sistemas de Numeración | Serie Computación y Programación #6

La Serie Computación y Programación en su primera edición, consiste en una entrega diaria, donde hablaremos de un tema, en la misma abordaremos los aspectos teóricos, y abordaremos algunos ejemplos con el fin de ejemplificar y explicar como usar el tema explicado en la publicación. La misma está dirigida al público en general, pero con especial atención a estudiantes universitarios, que deseen estudiar o estudien computación, ingeniería en computación y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

El Algoritmo de la División o Algoritmo de Euclides
La división es una de las operaciones básicas de la aritmética, la misma consiste en determinar la cantidad de veces que un número está contenido en otro. Ella se puede ver desde el punto de vista algebraico como la operación inversa del producto, o lo que es lo mismo, se puede considerar como una resta repetida, donde el primer número se llama divisor, el segundo dividendo y el resultado se denomina cociente.
Ahora, cuando el divisor no está contenido un número exacto de veces en el dividendo, al operar se obtiene un nuevo término al que llamamos resto o residuo.
Formalmente, el Algoritmo de la División lo podemos enunciar de la siguiente manera:

El cual también podemos expresar de las tres formas siguientes:
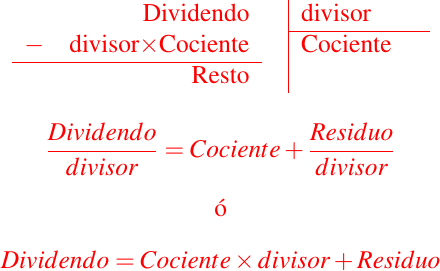
Podemos entonces clasificar las divisiones según sus restos: si el resto es cero, se dice que la división es exacta, y si es resto es distinto de cero se dice que la división es inexactas.
Así, diremos que un número natural a divide a un número natural b o que a
es un divisor de b, y lo denotamos por:

si existe un número natural c tal que

Por ejemplo, 7 divide a 28, ya que existe un número 4, tal que 28=7x4.
En caso contrario, decimos que a no divide a b, si no existe tal número c, y lo denotamos por:

Por ejemplo, 7 no divide a 30, ya que no existe un número C, tal que 30=7xC.
Luego, dado cualquier número natural a se tiene que

donde a los divisores 1 y a son llamados divisores triviales de a.

Ejemplo 01: Describir el algoritmo para dividir dos números, por ejemplo, 8593 (dividendo) y 23 (divisor).
- Iniciemos, escribiendo el dividendo a la izquierda y el divisor a la derecha de una escuadra o galera abierta hacia la derecha. Tal y como lo vimos anteriormente, lo cual podemos ver a continuación:
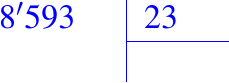
- Luego, tomamos la primera cifra del dividendo (8) y la dividimos por la primera del divisor (2) (en el caso de que la primera cifra del dividendo sea menor que la del divisor, tomamos dos cifras del dividendo); y buscamos el máximo cociente que multiplicado por el divisor sea menor que las dos (o tres, según sea el caso) primeras cifras del dividendo, de la forma siguiente:

ahora, como 92 es mayor que 85, tomamos una unidad inferior (3) y realizamos el producto con el divisor
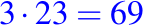
como 69 es menor que 85, restamos este producto obtenido de las dos primeras cifras (o tres, según sea el caso) del divisor
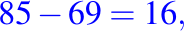
y escribimos la resta debajo de esa columna.
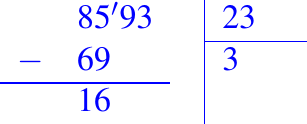
Entonces, agregamos a este resto la siguiente cifra del dividendo (9), y procedemos de la misma manera que con las dos primeras cifras con el nuevo número (169). Así sucesivamente con el resto de las cifras del dividendo.
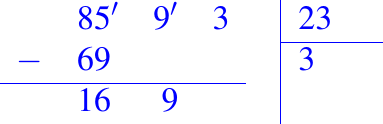
- Como 1 es menor que 2, tomamos las dos primeras cifras del número 169, efectuamos la división

debido a que 169 es menor que 184, multiplicamos por una unidad menor (7),
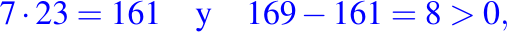
escribimos la resta debajo de esa columna.
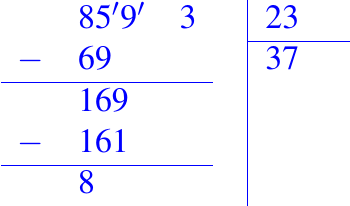
- Ahora seguimos con el siguiente dígito del dividendo (3) y consideramos el número 83.
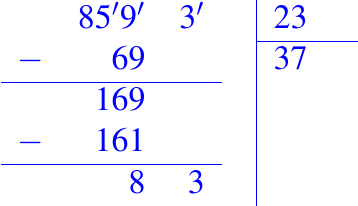
como

multiplicamos por 3 en vez de 4, esto es,

Al no tener más dígitos el dividendo, el resto es 14, el cual siempre debe ser menor que el divisor.

- Para terminar, el resultado es el siguiente: 8593 dividido por 23 nos da un cociente de 373 y un resto de 14; que se verificar por:
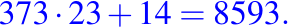

Queridos amigos y lectores, espero hayan disfrutado de esta sesta entrega de la serie de Computación y Programación, de igual manera los invito para la próxima entrega de esta serie, donde continuaremos tratando este tan bonito tema de los sistemas de numeración y otros aspectos. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la computación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias.
- Knuth, Donald Ervin. The art of computer programming. Vol. 1, 2, y 3. Pearson Education, 1997.
- Knuth, Donald Ervin. Fundamental algorithms: the art of computer programming. 1973.
- Knuth, Donald Ervin. Computer programming as an art. ACM Turing award lectures. ACM, 2007.
- von zur Gathen, Joachim and Gerhard, Jürgen. The Euclidean Algorithm. Modern Computer Algebra. Cambridge University Press, 2003.
También los invito a leer las anteriores publicaciones de está serie de Computación y Programación, que estoy seguro serán de su interés:
| Sistemas de Numeración #1 | Sistemas de Numeración #2 |
|---|---|
| Sistemas de Numeración #3 | Sistemas de Numeración #4 |
| Sistemas de Numeración #5 |
Todas las ecuaciones fueron creadas y editadas por @abdulmath con  , y GIMP.
, y GIMP.

Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.
God bless you. https://steemit.com/@biblegateway
Continuamos aprendiendo. Éxitos por tu esfuerzo y trabajo continuo. Un abrazo,
Buena vibra.
Hola @angelica7, gracias por tus palabras. Seguimos en la línea de trabajo. Saludos y exitos
Que bueno eres...
Hola @vidaparasita, gracias por visitarme y tus palabras. Saludos
Saludos amigo @abdulmath, por acá leyéndole
Saludos @lupafilotaxia. Gracias por leerme, saludos y un abrazo.
Como siempre, excelente reseña!!... gracias ;);)
Hola @adri525, gracias. Saludos.
muy bueno tu trabajo profe
Hola @duque, muchas gracias. Siempre dando un extra. Saludos y un abrazo
Felicitaciones por tu trabajo y constancia.
Gracias @rmartinezpoeta por tu estimulo y ánimos. Saludos y un abrazo.
Difusión del conocimiento vital para quienes se adentran en el mundo de los ordenadores..! ¡Votado por Engranaje!
Muchas gracias por el apoyo. Saludos