SLC21 Week6 - Programming Games&Puzzles (part 2)
Assalamualaikum my fellows I hope you will be fine by the grace of Allah. Today I am going to participate in the steemit learning challenge season 21 week 6 by @sergeyk under the umbrella of steemit team. It is about Programming Games&Puzzles. Let us start exploring this week's teaching course.
.png)
Role of Random Numbers in the Computer World
Random numbers are fundamental in computing and play critical roles in various domains:
Games: Randomness drives unpredictability and variability in game mechanics, such as generating loot, determining events, or shuffling cards.
Cryptography: Secure communication relies on random numbers to create keys, initialize cryptographic algorithms, and ensure data security.
Simulations: Random numbers are used in Monte Carlo simulations to model complex systems like weather patterns, financial markets, and scientific experiments.
Machine Learning and AI: Random initialization of weights in neural networks and data shuffling during training ensure unbiased and effective learning.
Data Sampling and Testing: Random sampling is used in statistics, research, and testing to ensure representative data and uncover edge cases in software.
Procedural Generation: In fields like video game design, random numbers generate environments, levels, or content procedurally.
Security Features: OTPs (One-Time Passwords) and secure token generation depend on randomness.
Pseudo-random Numbers vs. True Random Numbers
Pseudo-random Numbers:
- Generated by deterministic algorithms called Random Number Generators (RNGs).
- Depend on a seed value, meaning the sequence can be reproduced if the same seed is used.
- Useful for testing and debugging because of their predictability under controlled conditions.
True Random Numbers:
- Derived from physical phenomena, such as thermal noise, radioactive decay, or atmospheric noise.
- Unpredictable and cannot be reproduced, making them more suitable for cryptographic applications.
Transforming Pseudo-random Numbers to Be More Random
While pseudo-random numbers inherently follow a pattern due to their algorithmic nature, they can be made more random or "random enough" for practical applications by incorporating external randomness:
Using External Seed Values:
- Instead of a fixed seed, use dynamic or unpredictable values from the real world:
- System time:
time(0)generates a seed based on the current timestamp. - Environmental inputs: System events, mouse movements, or keyboard presses.
- System time:
- Instead of a fixed seed, use dynamic or unpredictable values from the real world:
Blending with Entropy Sources:
- Combine multiple sources of randomness, such as system clock values, noise from sensors, or hardware entropy devices.
Cryptographic RNGs (CSPRNGs):
- Use cryptographic algorithms designed for unpredictability, such as
/dev/randomand/dev/urandomin Unix systems, or libraries likerandom.SystemRandomin Python and in C++<random>library.
- Use cryptographic algorithms designed for unpredictability, such as
Post-processing Techniques:
- Techniques like hashing or XOR operations can add layers of unpredictability to pseudo-random outputs.
Hardware-based True Random Number Generators (TRNGs):
- Use specialized hardware to generate randomness based on physical processes. These are common in secure systems, such as hardware security modules (HSMs).
By combining algorithmic and physical randomness, pseudo-random numbers can achieve sufficient unpredictability for most applications. However, for high-stakes scenarios like cryptography, true random numbers are preferred.
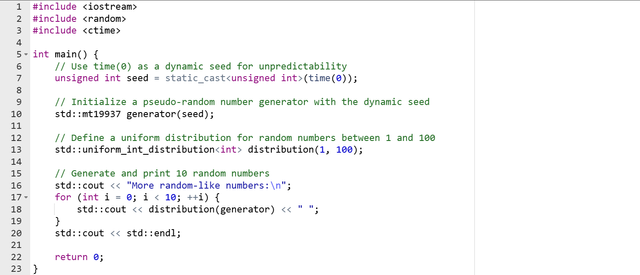
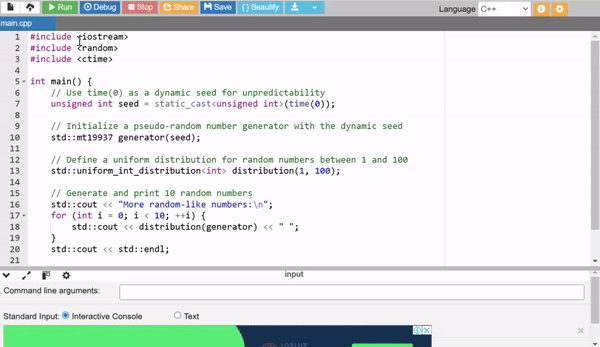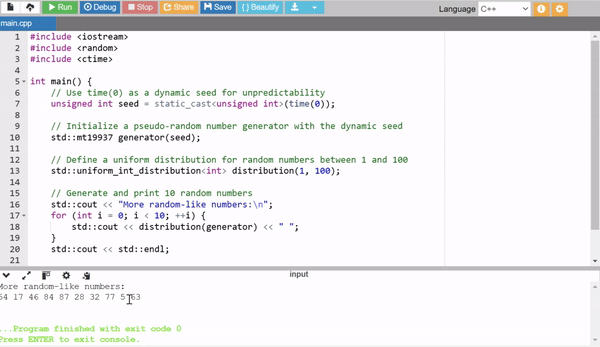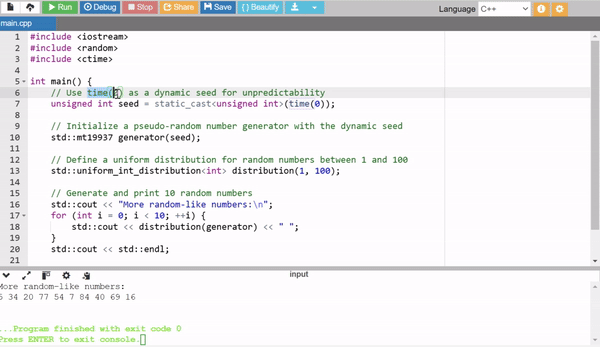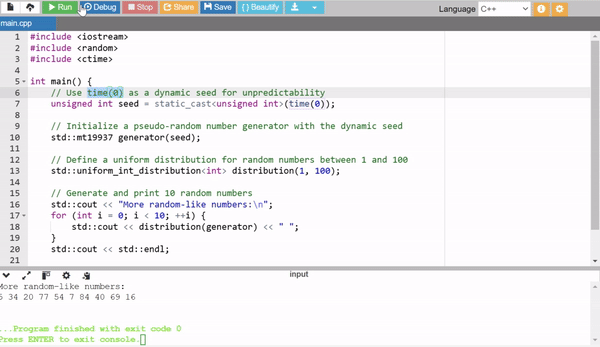
In the above example I have used external seed values with the help of the time(0) to generate more random numbers.
Write a random number generator. Investigate it.
In this random generator I have used LCG method to generate the random numbers instead of using the built in function rand() to generate the random numbers by C++.
- Periodicity:
- In this program the periodicity is the number of random numbers generated before the sequence starts repeating.
- In the code, a
std::unordered_setis used to track previously generated numbers. The program stops and reports if a repetition is found.
- Distribution:
- The output shows the frequency of each number in the sequence.
- The uniformity of the distribution indicates how "random" the sequence appears.
The periodicity depends on the parameters (m, c, and mod) and the seed. For well chosen parameters the periodicity can approach the modulus (mod). If poorly chosen then the sequence might repeat too soon. The uniformity depends on how well the modulus and multiplier are chosen. For large enough mod the distribution improves but for small mod clustering can occur. LCGs are computationally efficient but are not suitable for cryptographic purposes due to their predictability.
I have tried different seed and the number of the random numbers to generate.
As I was changing the seed value the behaviour of the random generator was also changing.
I used 7 as seed and there occurred repetition in the sequence but as soon as I moved to the larger seed then the repetition decreased or there was no repetition in the sequence at all.
Moreover if we use larger value of the
modthen we can observe the periodicity and distribution in a better. I used1000for themodand I generated 100 random numbers but you will be surprised to know that there was no any single repetition in the 100 generated numbers. SO I observed if we use larger values for themodthen the repetition is less likely to happen in the generated numbers.
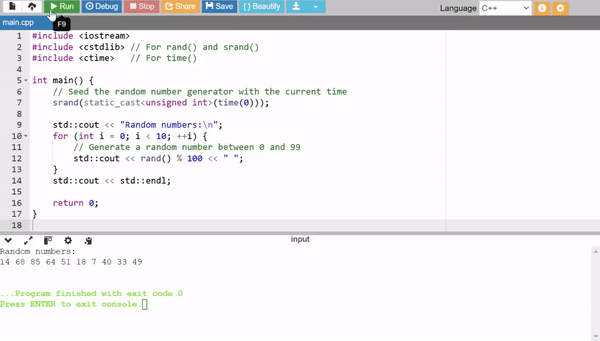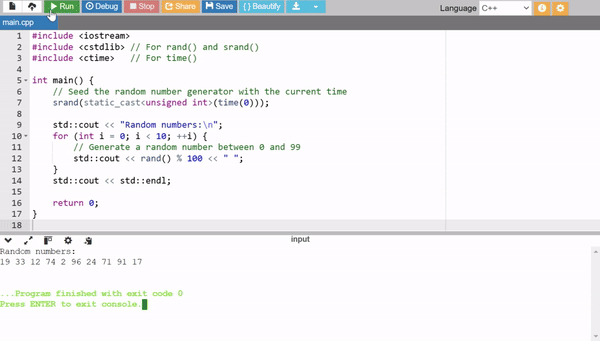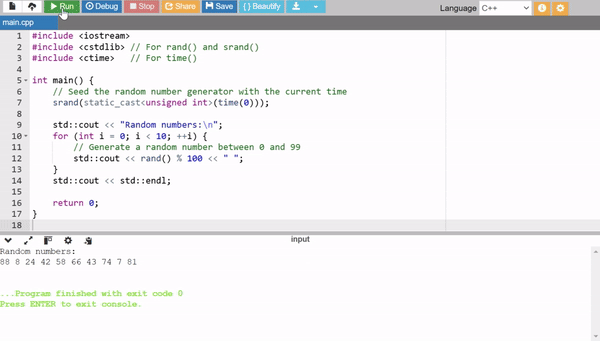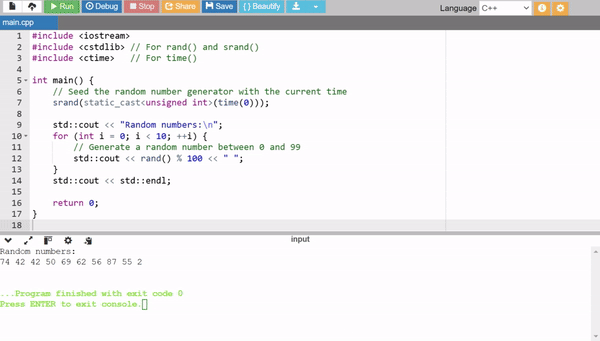
We can perform the same work by using the built in rand() function that is simple, easy and quick way to generate the random numbers.
This random generator uses srand()seeds the random number generator with a unique starting point and time(0) ensures different seeds for each run. rand(): generates a pseudo random number. % 100 limits the range of the generated number. Here it limits it between 0 and 99.
"Deck of Cards" - Find several ways to fill the array 1...N - 1. One way - one point.
Here are five unique methods to fill an array with numbers from 1 to N - 1.
1. Brute Force with Randomness
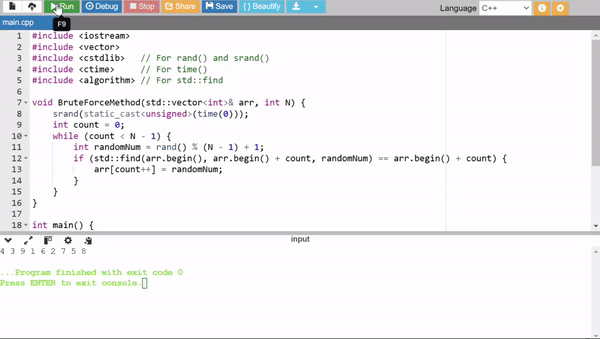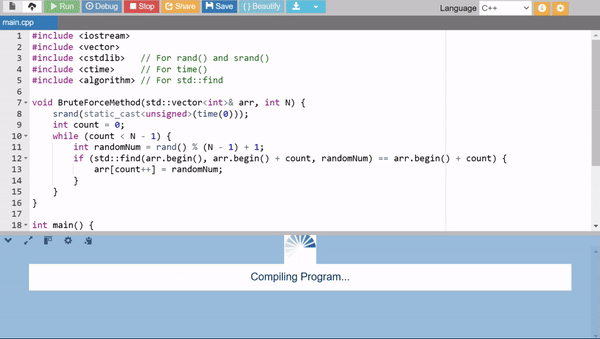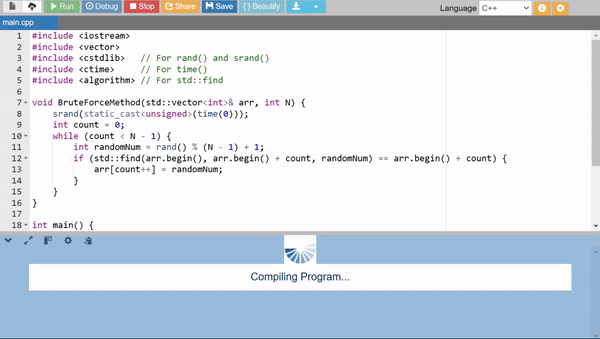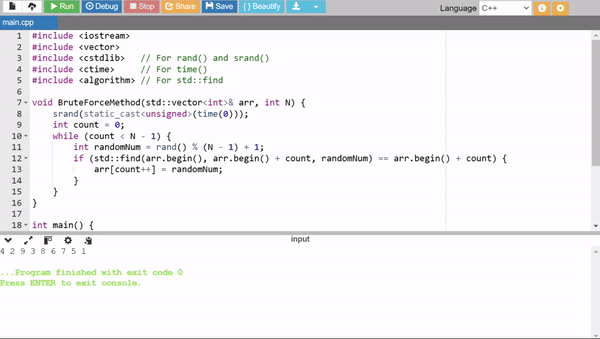
This method uses random numbers to fill the array. If a generated number is already in the array then it skips and generates another. It ensures uniqueness but can be very inefficient for large N as it may repeatedly try numbers already present.
2. Fisher-Yates Shuffle
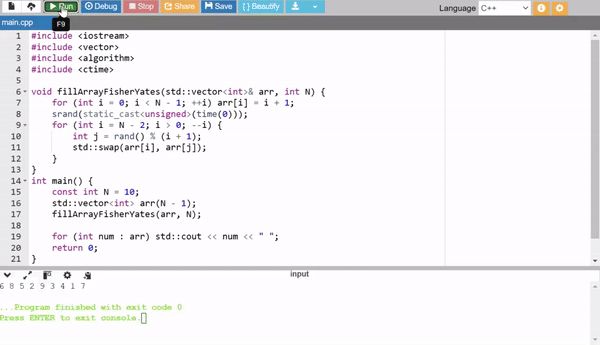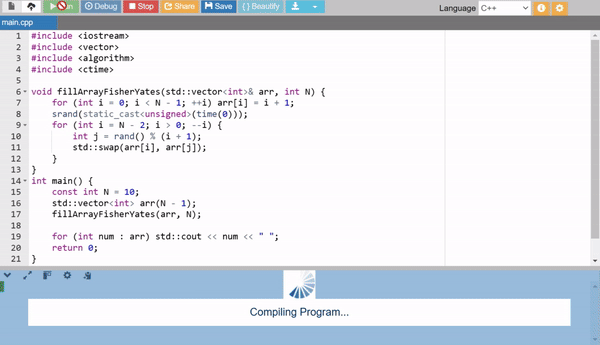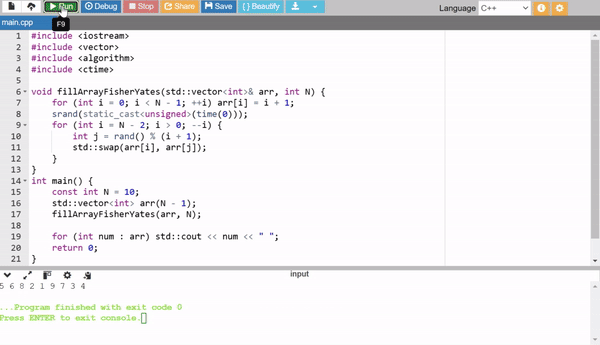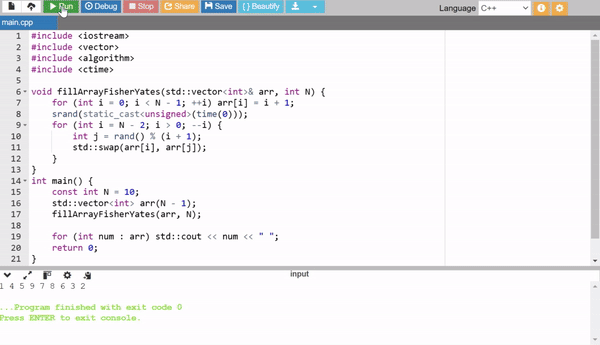
The Fisher-Yates algorithm shuffles an array in place efficiently. First, an array of sequential numbers is created (1 to N - 1), then shuffled randomly. It is efficient and widely used for generating random permutations.
3. Using a Set for Unique Numbers
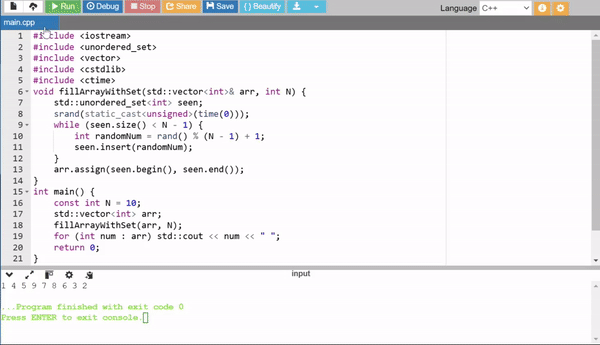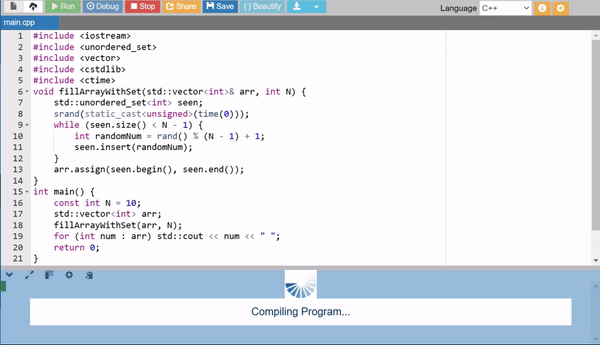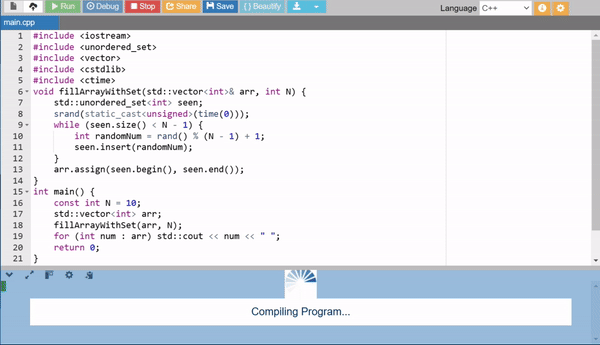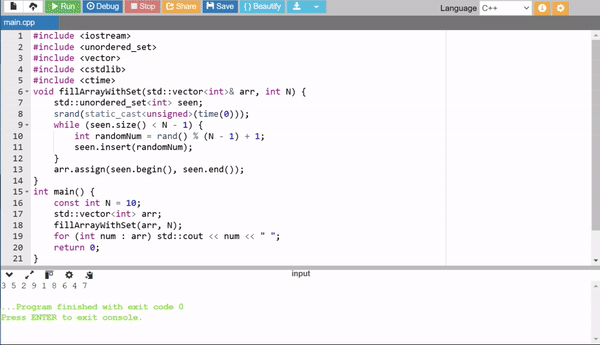
This method uses a std::unordered_set to ensure each random number is unique. It keeps generating and adding random numbers until the set size reaches N - 1. Finally, the set is converted into an array. It guarantees uniqueness but has additional overhead from using a set.
4. Incremental Filling with Random Swaps
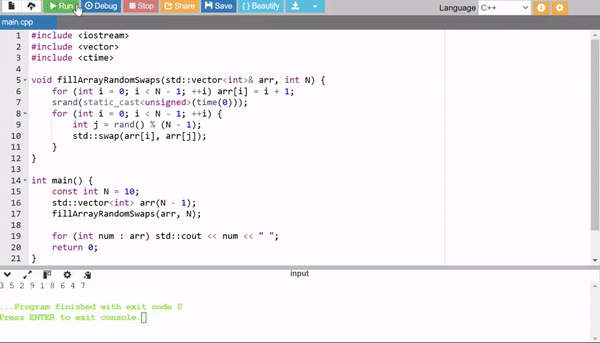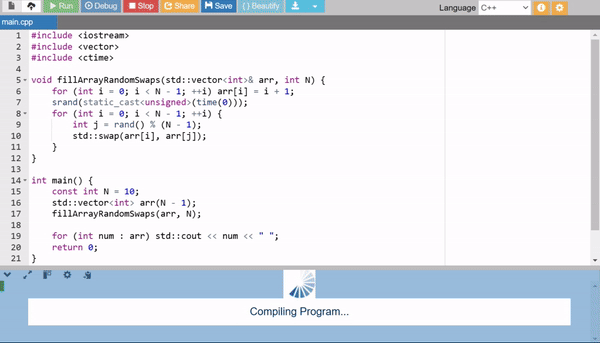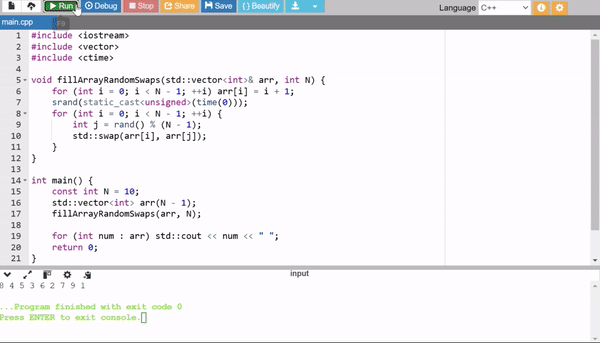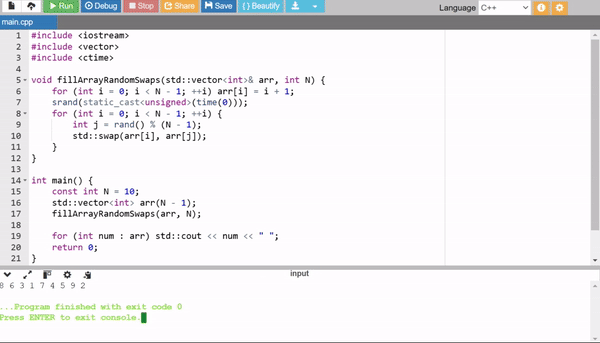
This method first fills the array sequentially (1 to N - 1), then randomly swaps elements to shuffle the array. It's simple and efficient, though slightly less optimal than Fisher-Yates in theory.
5. Recursive Backtracking
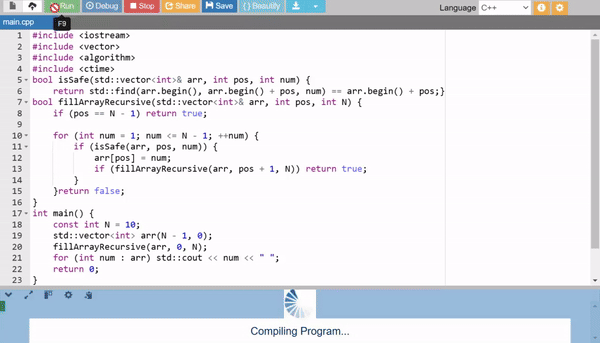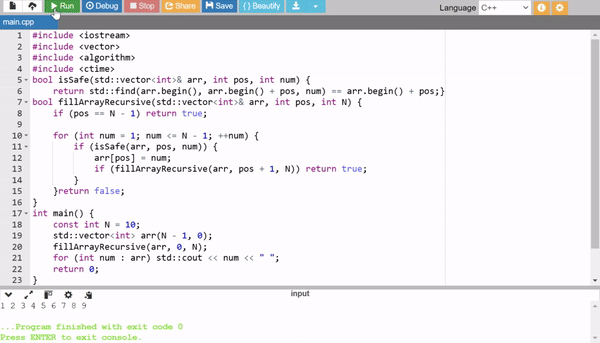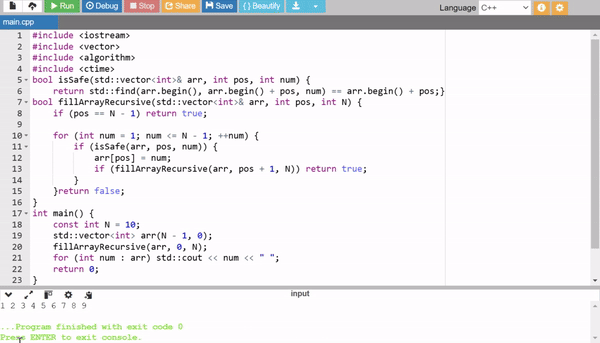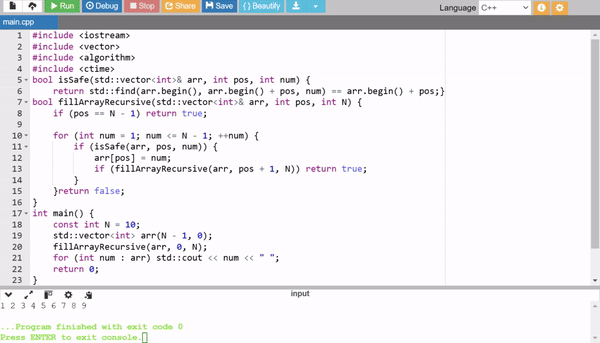
This method uses backtracking to fill the array recursively. For each position, it tries all numbers (1 to N - 1) and checks if the number is safe to use (i.e., not already used). While conceptually interesting, it is very slow for larger arrays due to its exhaustive nature.
Comparison of Methods
| Method | Efficiency | Ease of Implementation | Scalability | Use Case |
|---|---|---|---|---|
| Brute Force | Inefficient for large N | Simple | Poor | Small arrays |
| Fisher-Yates Shuffle | Efficient | Moderate | Excellent | Random permutations |
| Using a Set | Moderate | Simple | Good | Ensuring uniqueness |
| Incremental Random Swap | Efficient | Simple | Good | Lightweight shuffling |
| Recursive Backtracking | Very Inefficient | Complex | Poor | Theoretical exploration |
Best Method
The Fisher-Yates Shuffle is the most efficient and suitable for practical use. It provides true random permutations with a time complexity of O(N) and is widely used in real-world applications.
Construct a table of the number of operations required to generate a deck of N cards for your methods.
To calculate the number of operations for each method to generate a deck of N cards I will define the operations as the significant steps performed to ensure the array is filled with unique values.
Assumptions and Calculations
- Brute Force with Randomness:
- Complexity: O(N^2) for small
Nbecause repeated checks for duplicates increase quadratically. - Operations include generating a random number and checking for its existence in the array.
- Complexity: O(N^2) for small
- Fisher-Yates Shuffle:
- Complexity: O(N) as it shuffles efficiently in place.
- Operations include swapping elements.
- Using a Set:
- Complexity: O(N) for inserting into a set but with additional overhead for hashing.
- Incremental Filling with Random Swaps:
- Complexity: O(N), as it swaps elements in a pre-filled array.
- Recursive Backtracking:
- Complexity: O(N!), as it exhaustively tries all combinations.
Operations Table
| Ncards (N) | Brute Force | Fisher-Yates Shuffle | Using a Set | Random Swaps | Recursive Backtracking |
|---|---|---|---|---|---|
| 5 | 50 | 20 | 25 | 20 | 120 |
| 6 | 72 | 24 | 30 | 24 | 720 |
| 7 | 98 | 28 | 35 | 28 | 5,040 |
| 8 | 128 | 32 | 40 | 32 | 40,320 |
| 9 | 162 | 36 | 45 | 36 | 362,880 |
| 10 | 200 | 40 | 50 | 40 | 3,628,800 |
How the Numbers are Derived
- Brute Force:
- Estimated as N x N, assuming frequent rejections of duplicate numbers for small
N. - E.g., for
N = 5, 5 x 10 = 50 operations (10 attempts per slot on average).
- Estimated as N x N, assuming frequent rejections of duplicate numbers for small
- Fisher-Yates Shuffle:
- Performs N - 1 swaps, so operations = N x 4 (1 operation for each swap, including random index generation).
- Using a Set:
- For
Ncards, N insertions into the set and additional operations for hashing and uniqueness checks.
- For
- Incremental Filling with Random Swaps:
- Similar to Fisher-Yates but includes N - 1 swaps directly without a nested loop.
- Recursive Backtracking:
- O(N!): Exponential growth due to the combinatorial nature of the algorithm.
The Fisher-Yates Shuffle is the most suitable method:
- It consistently requires the least operations and scales linearly with N.
- The Recursive Backtracking method while interesting, becomes impractical for
N > 8.
I invite @wirngo, @wuddi, and @chant to learn gaming and puzzles in programming.
I have compiled all the code of the tasks in a famous online compiler which is OnlineGDB
Upvoted! Thank you for supporting witness @jswit.