SEC-S20W3 Writing the first code
 |
|---|
Hello Steemians, welcome to my post and stay safe as you read through this post.
Online compiler (IDE)
Online compilers (IDE) are many and to choose an online (IDE) for C++ or any other programming language I will need to search for a reliable language and identify the key elements. The steps below are the processes that I will need to follow to get reliable results.
To search for an online C++ compiler, I will need to go to a search engine and search or type in **"Online C++ compiler" where I will then see some options like; **ideone.com, OnlineGDB, jdopdle.com, etc. Having said so, I will then choose a compiler based on first impression for example, OnlineGDB which is user-friendly as it is for beginners who want to learn about C++.
The next is the identification of the key elements after I have chosen my compiler, which in this case the following are what are found when using OnlineGDB.
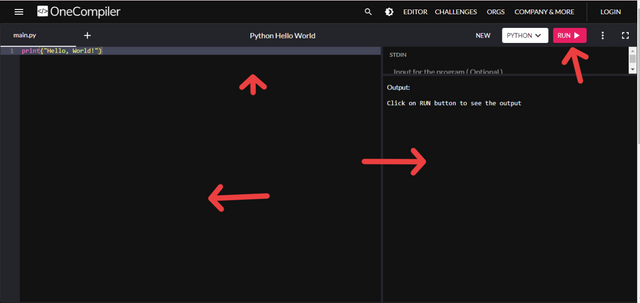
From the above screenshot, you can see , Code entry window which is where C++ code can be written, Output window which is the result of our program is been display which is seen below the right of the code entry window. RUN Button is the button that starts the execution of our code which is seen located above the code entry window at the top right-hand side as Run. The Data entry window is what allows us to enter our input data so the program can read it while running.
Lesson should be completed in three versions
Finding your way to act, from 1 to 100 effective or not in this task is not important.
For me to solve the problem of transforming 1 into 100 using only the operations "+1" (add 1) and "×2" (multiply by 2), I will first need to find the sequences of operations that result in 100. Below are the three different versions that I used and some of these challenges.
Version 1
In this version, I make use of prioritizing multiplication by 2 which is a strategy that focuses on using multiplication by 2 as long as possible before 1 can be added to reach 100 at a dot. Here what I did was to break down the process mathematically as shown below.
Multiply by 2
1 × 2 = 2
Multiply by 2
2 × 2 = 4
Multiply by 2
4 × 2 = 8
Multiply by 2
8 × 2 = 16
Multiply by 2
16 × 2 = 32
Multiply by 2
32 × 2 = 64
After doing the above calculation if I should continue further my answer would become more than 100 which I have to stop and apply the addition of 1.
Add 1
64 + 1 = 65
Add 1
65 + 1 = 66
Add 1
66 + 1 = 67
Add 1
67 + 1 = 68
Add 1
68 + 1 = 69
Add 1
69 += 70
:Add 1
70 + 1 = 71
Add 1
71 + 1 = 72
Add 1
72 + 1 = 73
Add 1
73 + 1 = 74
Add 1
74 + 1 = 75
Add 1
75 + 1 = 76
Add 1
76 + 1 = 77
Add 1
77 + 1 = 78
Add 1
78 + 1 = 79
Add 1
79 + 1 = 80
Add 1
80 + 1 = 81
Add 1
81 + 1 = 82
Add 1
82 + 1 = 83
Add 1
83 + 1 = 84
Add 1
84 + 1 = 85
Add 1
85 + 1 = 86
Add 1
86 + 1 = 87
Add 1
87 + 1 = 88
Add 1
88 + 1 = 89
Add 1
89 + 1 = 90
Add 1
90 + 1 = 91
Add 1
91 + 1 = 92
Add 1
92 + 1 = 93
Add 1
93 + 1 = 94
Add 1
94 + 1 = 95
Add 1
95 + 1 = 96
Add 1
96 + 1 = 97
Add 1
97 + 1 = 98
Add 1
98 + 1 = 99
Add 1
99 + 1 = 100
The above problem can be solved in three different ways using the allowed operations (+1 and ×2).
Find the best, shortest way. No one found it in the last lesson. Search!
Here you will see that I have made my steps shorter to reach 100 than the previous steps that I took at first. Here I tried more ways before arriving at the answer100 which I did here was starting with +1 into 3 before I then begin to multiply by ×2 as shown below.
1+1 = 2
2 +1 = 3
3 * 2 = 6
6 * 2 = 12
12 * 2 = 24 +1 = 25
25 * 2 = 50
50 * 2 = 100
Breakdown
Add 1
1+1 = 2
Add 1
2 + 1 = 3
Multiply by 2
3 × 2 = 6
Multiply by 2
6× 2 = 12
Multiply by 2
12 × 2 = 24
Add 1
24 + 1 = 25
Multiply by 2
25 × 2 = 50
Multiply by 2
50 × 2 = 100
While doing the calculation, I had to add +1 to 24 so I could multiply it by 2 which gave me 50 I then multiplied 50 by 2 which gave me 100. Had it been 1 wasn't added to 24, I wouldn't have arrived at this answer in the shortest time.
If in addition to +1 and x2it is possible to create an additional variable int k; how many steps will it save, you cannot put a certain number in the variable, for example, 7 or 23. You can only fix the value of the variable at a certain step n
Finding out how many steps will it save for is quite difficult as the introduction of variable K while reaching49 using only operations +1 and ×2, and fixing the value of the variable k at a certain step n
Steps without k
As we have earlier determined reaching 49 from 1 without any additional variables takes 22 steps and using +1 and ×2.
Introducing k
Here I cannot directly assign a specific value to k rather I can store the value of the sequence at any step n and use the value later for more efficient results. To this fixing the value of k at an optimal point in the sequence where it helps reduce the number of +1 operations is what I did.
1 × 2 = 2, 2 × 2 = 4, 4 × 2 = 8, 8 × 2 = 16, 16 × 2 = 32
Fix k = 32 at this point.
Now, using k to avoid unnecessary +1 operations
From 32 that is gotten, instead of me adding 17 more times to reach 49, I use k to have the number of additions.
The first thing I did was to add 16 quickly by multiplying it by 2 (32 ×2 = 64) and begin to adjust downward.
From this point, 32 × 2 = 64 which is an overshoot target, I then subtract 1 at each of the steps which isn't ideal for me.
To allow further addition k is set as 32.
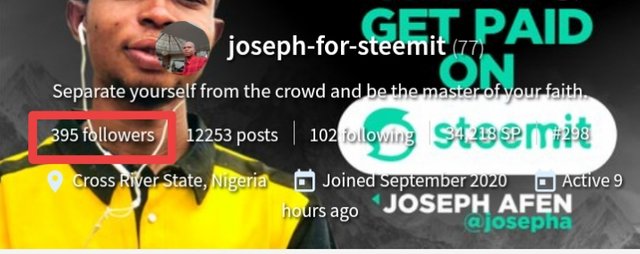
From the above image, I have a total of 395 followers, and taking the first two the number becomes 39. Based on the given requirement I have added 21 to the number which becomes 60.
For me to solve the task of reaching 60 from 1 using only +1 and ×2 operations I aim at using the shortest paths focusing on doubling as much as possible and using 1 where necessary.
1 × 2 = 2
2 × 2 = 4
4 × 2 = 8
8 × 2 = 16
16 × 2 = 32
32 × 2 = 64.
Subtracting 1 using +1 in reverse is not going to be possible in the current rules I took, which means the subtraction would be done gradually.
Degree
Take your number, I take my 49 and add its digits and also add 7: 4+9+7=16. We need to write a program to raise the number to the 16th power - all of you will have different numbers.
Here what I need is to write a program that raises my number which is 60 to the 18th power, as per the task where I will add my digits and 7.
Below is a Python program that calculates 60^18.
# Define the base number
number = 60
# Define the power
power = 18
# Calculate the result
result = number ** power
# Print the result
print(f"{number} raised to the power of {power} is: {result}")
Output
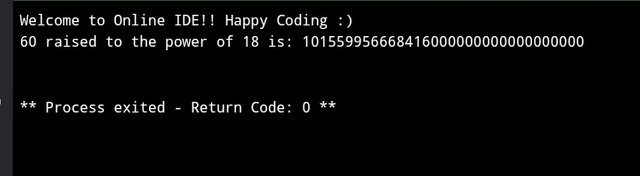
Interpretation
- The variable
numberis set to 60 - The
poweris 18, based on my given task. - The result is calculated using the
**operator, which raises the base to the specified power.
Write a program to divide it into numbers. And now how to collect it from numbers back into a number? How to reverse a number. In other words, unfold. For example, how to get 39 from 93.
This will be divided into two parts;
Dividing a number into its digits we are going to take a number and break it down into individual digits
Secondly, reversing numbers after breaking them down into digits, we can reverse those digits and reassemble them into a number example, 39 from 93.
Dividing a number into digits Python code
# Define the number
number = 60**18 # Or any number you wish to divide into digits
# Convert the number to a string to easily access its digits
digits = [int(digit) for digit in str(number)]
# Print the digits
print("Digits of the number:", digits)
Reversing the digits and assembling them back into a number
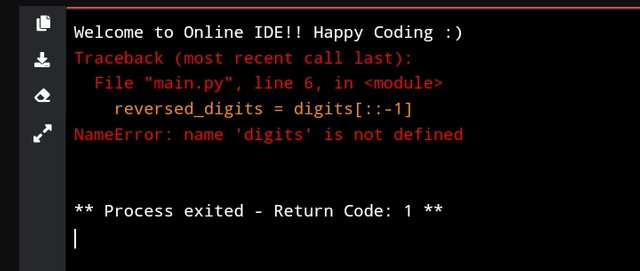
Once you have the digits of the number, reversing them is straightforward. Here's how to reverse and reassemble the number:
# Reverse the digits list
reversed_digits = digits[::-1]
# Convert the reversed digits back into a number
reversed_number = int(''.join(map(str, reversed_digits)))
# Print the reversed number
print("Reversed number:", reversed_number)
Reversing a number into digits Python code like 93
# Define the number
number = 93
# Convert the number to a string to break it into digits
digits = [int(digit) for digit in str(number)]
# Reverse the digits list
reversed_digits = digits[::-1]
# Convert the reversed digits back into a number
reversed_number = int(''.join(map(str, reversed_digits)))
# Print the reversed number
print("Reversed number:", reversed_number) # Output will be 39
Interpretation
- First is to convert the number into a string to access its digits easily
- Second is to convert back to an integer and store them in a list
- Thirdly to reverse the list of digits using slicing
- Fourthly, we add the reversed digits together and convert them back to an integer to get the reversed number.
Take the first three numbers from your profile (the number of followers or posts) - and divide it into numbers
Here I will take the first three digits from the number of followers from my profile image, which is 395.
Dividing the number 395 into its digits Python code
# Define the number
number = 395
# Convert the number to a string to easily access its digits
digits = [int(digit) for digit in str(number)]
# Print the digits
print("Digits of the number:", digits)
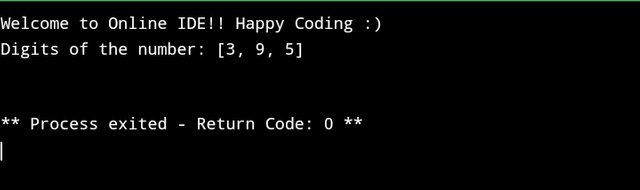
For 395, the digits would be:
- 3
- 9
- 5
Find a four-digit number in your profile (by writing out the first digits, or combining it with others, the first two of one and the first two of another.) Or a random number - the main thing is that it is not in other homework. Divide it into numbers - the first number is X, the second number is X, the third number is X, the fourth number is X
Here I take the first two digits from the number of my followers 395 and the first two digits from the number of posts 12253 on my profile image.
Combining the first two digits from each:
- From followers 39
- From posts 12.
That above will give us a digit number as 3912.
Diving the number 3912 into its digits I will have the following.
- X = 3
- X = 9
- X = 1
- X = 2
I am inviting: @dove11, @simonnwigwe, and @lhorgic
Cc:-
@sergeyk
Upvoted. Thank You for sending some of your rewards to @null. It will make Steem stronger.