Il sistema eliocentrico di Aristarco

Aristarco di Samo, (nato c. 310 AC – morto c. 230 AC ) fu un astronomo greco che sosteneva che la Terra ruotasse sul proprio asse e attorno al Sole . Su questa base, il filosofo greco  fu incriminato per empietà “per mettere in moto il cuore dell’universo “. Il lavoro di Aristarco sul moto della Terra non è sopravvissuto, ma le sue idee sono note dai riferimenti del matematico greco Archimede , il biografo greco Plutarco e il filosofo greco Sesto Empirico.  Archimede disse nella suaSand-Reckoner che Aristarco aveva proposto una nuova teoria che, se fosse vera, avrebbe reso l’universo enormemente più grande di quanto si credesse. (Questo perché una Terra in movimento dovrebbe produrre una parallasse, o spostamento annuale, nelle posizioni apparenti delle stelle fisse, a meno che le stelle non siano davvero molto lontane.)Nel XVI secolo Aristarco fu una fonte d’ispirazione per l’astronomo polacco Il lavoro di Nicolaus Copernico . Nel suo manoscritto di Sei libri riguardanti le rivoluzioni delle sfere celesti (1543), Copernico citò Aristarco come un’antica autorità che aveva sposato il moto della Terra. Tuttavia, in seguito Copernico cancellò questo riferimento e la teoria di Aristarco non fu menzionata nel libro pubblicato.L’unica opera esistente di Aristarco è  Sulle dimensioni e le distanze del Sole e della Luna , il più antico trattamento geometrico sopravvissuto di questo problema. Aristarco prende come premesse:

• (1) come osservato durante un’eclissi lunare , il diametro dell’ombra della Terra è il doppio del diametro della Luna ;
• (2) la Luna e il Sole sono ciascuno di 2 gradi di diametro angolare; e
• (3) al momento del quarto di luna, la distanza angolare tra la Luna e il Sole è di 87 gradi.

Usando la premessa 3, Aristarco mostrò che il Sole è tra 18 e 20 volte più lontano dalla Terra di quanto lo sia la Luna. (Il rapporto effettivo è circa 390.) Usando questo risultato e le premesse 1 e 2 in una costruzione geometrica intelligente basata su eclissi lunari, ha ottenuto valori per le dimensioni del Sole e della Luna. Ha trovato che il diametro della Luna è compreso tra 0,32 e 0,40 volte il diametro della Terra e il diametro del Sole deve essere compreso tra 6,3 e 7,2 volte il diametro della Terra. (I diametri della Luna e del Sole confrontati con quelli della Terra sono in realtà rispettivamente 0,27 e 109).Ai tempi di Aristarco il metodo geometrico era considerato più importante delle misure numeriche. La sua premessa 1 è ragionevolmente accurata. Premessa 2 sovrastima il diametro angolare della Luna di un fattore quattro, il che è sconcertante, poiché questa è una misura facile da fare. (In una pubblicazione successiva, Aristarco diede la metà della misura angolare della Luna, che è giusto, ma apparentemente non modificò il suo lavoro precedente.) Premessa 3 non era probabilmente basata sulla misurazione, ma piuttosto su una stima; equivale a supporre che il tempo dal primo quarto di luna al terzo quarto di luna sia un giorno più lungo del tempo dal terzo al primo quarto. Il vero angolo tra Sole e Luna al momento del quarto di luna è meno di 90 gradi per soli 9 minuti di arco, una quantità impossibile da misurare nell’antichità.Più tardi gli astronomi greci, in particolare Ipparco e Tolomeo , raffinarono i metodi di Aristarco e raggiunsero valori molto accurati per le dimensioni e la distanza della Luna. Tuttavia, a causa dell’influenza della premessa 3, tutti i risultati antichi hanno grossolanamente sottostimato le dimensioni e la distanza del Sole. Il rapporto 19: 1 di Aristarchus rimase tuttavia più o meno standard fino al 17 ° secolo.Aristarco di Samo non sembra aver avuto l’attenzione degli storici della matematica che meritava fino a tempi recenti. Ad esempio, Heath inizia il Volume II della sua storia della matematica greca con le parole [ 5 ]: – Gli storici della matematica hanno, di regola, dato troppa poca attenzione a Aristarco di Samo. Il motivo è senza dubbio che era un astronomo, e quindi si potrebbe supporre che il suo lavoro non avrebbe interesse sufficiente per il matematico. I greci sapevano meglio; lo chiamavano “Aristarco il matematico”.
Tuttavia il fatto che fosse conosciuto come astronomo piuttosto che come matematico è piuttosto neutralizzato dalla tesi di Neugebauer che il suo lavoro [ 6 ]: – … è un esercizio puramente matematico che ha … poco a che fare con l’astronomia pratica … Zhitomirskii, in [ 14 ], afferma: – Aristarco di Samo è un precursore poco noto ma spesso citato di Copernico . Tutte le informazioni su di lui derivano da una manciata di riferimenti sparsi negli scrittori classici, oltre a un suo breve trattato che non menziona l’eliocentrismo. Di conseguenza gli storici spesso lo citano, citano uno o due fatti e passano a un altro argomento – dopo aver fornito alcune parole di spiegazione che rivelano molto sui pregiudizi degli storici.
Il documento [ 14 ] quindi fa un serio tentativo di rimediare a ciò che l’autore ritiene essere le carenze di altri storici. Cerchiamo in questo articolo di fare più che “menzionare uno o due fatti” e di indicare sia la grandezza e l’originalità delle conquiste di Aristarco, sia il suo ruolo nello sviluppo dell’astronomia matematica.
Aristarco era certamente sia un matematico che un astronomo ed è il più celebrato come il primo a proporre un universo centrato sul sole. È anche famoso per il suo tentativo pioneristico di determinare le dimensioni e le distanze del sole e della luna. Daremo un’occhiata a questi due risultati qui sotto.Aristarco era uno studente di Strato di Lampsaco, che era a capo del Liceo di Aristotele . Tuttavia, non si pensa che Aristarco abbia studiato con Strato ad Atene, ma piuttosto che abbia studiato con lui ad Alessandria. Strato divenne capo del Liceo di Alessandria nel 287 aC e si pensa che Aristarco studiò con lui lì iniziando i suoi studi poco dopo quella data.Aristarco è menzionato da Vitruvio ( I secolo aC) famoso come architetto e ingegnere romano. Vitruvio fu l’autore dell’enorme trattato De architectura (in architettura) e in questo lavoro elenca uomini che sono stati ben informati in tutti i rami della scienza (si veda ad esempio [ 3 ], [ 4 ] o [ 5 ]): –
Uomini di questo tipo sono rari, uomini come lo erano, in passato, Aristarco di Samo, Filolao e Archita di Taranto, Apollonio di Perga, Eratostene di Cirene, Archimede e Scopine di Siracusa, che lasciarono ai posteri molti apparecchi meccanici e gnomonici che hanno inventato e spiegato su principi matematici.
Naturalmente c’è la domanda immediata di ciò che Aristarco ha inventato, e Vitruvio spiega che ha inventato una meridiana a forma di scodella emisferica con un puntatore per gettare ombre poste al centro della ciotola.
Esistono poche prove esistenti sull’origine della credenza di Aristarco in un sistema eliocentrico . Non sappiamo di nessuna ipotesi precedente di questo tipo, ma in realtà la teoria non è stata accettata dai greci, quindi apparentemente non ha mai avuto alcuna popolarità. Sappiamo solo della teoria di Aristarco a causa di una dichiarazione sommaria fatta in Archimede ‘ The Sand-Reckoner e un riferimento simile da Plutarco . Archimede ha scritto (vedi per esempio [ 3 ], [ 4 ] o [ 5 ], o vedi [ 1 ] per una citazione più breve): –
Tu, Re Gelon, sei consapevole che “l’universo” è il nome dato dalla maggior parte degli astronomi alla sfera il cui centro è il centro della terra, mentre il suo raggio è uguale alla linea retta tra il centro del sole e il centro della terra. Questo è l’account comune come hai sentito dagli astronomi. Ma Aristarco ha tirato fuori un libro composto da alcune ipotesi, in cui appare, come conseguenza delle supposizioni fatte, che l’universo è molte volte più grande dell’universo appena menzionato. Le sue ipotesi sono che le stelle fisse e il sole rimangono immutati, che la terra ruota intorno al sole sulla circonferenza di un cerchio, il sole che giace nel centro dell’orbita, e che la sfera di stelle fisse, situata sullo stesso centro come il sole,
Archimede, avendo riportato le opinioni di Aristarco, criticò quelle vedute come proporzioni matematicamente prive di significato. In realtà il modo in cui Aristarco esprime le sue proporzioni è, secondo Heath , simile ad altre espressioni che si verificano negli scritti greci e indica che Aristarco riteneva che il raggio della sfera delle stelle fisse fosse infinitamente grande rispetto all’orbita della terra. Certo, Aristarco doveva fare una tale ipotesi, perché altrimenti sarebbero visibili gli effetti di parallasse .
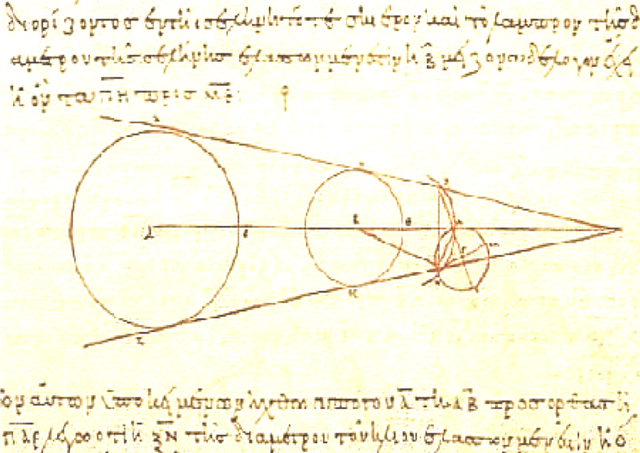
Plutarco ci dà qualche informazione in più, poiché riferisce che Aristarco seguì Eraclide del Ponto nel credere che l’apparente rotazione quotidiana delle stelle fisse fosse dovuta alla rotazione della terra sul suo asse.L’unica opera superstite di Aristarco, Sulle dimensioni e le distanze del Sole e della Luna , non è basata sulla teoria centrata sul sole e sfortunatamente il suo lavoro su quella teoria centrata sul sole a cui ha fatto riferimento Archimede è andato perduto. Sulle dimensioni e le distanze del Sole e della Luna fornisce i dettagli del suo ragionamento geometrico notevole, basato sull’osservazione, per cui ha determinato che il Sole era circa 20 volte più lontano dalla Terra come la Luna, e 20 volte la dimensione della Luna. Entrambe queste stime erano di un ordine di grandezza troppo piccolo, ma la colpa era nella mancanza di strumenti precisi di Aristarco piuttosto che nel suo corretto metodo di ragionamento.Il diagramma mostra un argomento usato da Aristarco. Sapeva che la luna brilla di luce solare riflessa, così sostenne, se si misurasse l’angolo tra la luna e il sole quando la luna è esattamente a metà illuminata, allora si potrebbe calcolare il rapporto delle loro distanze. Aristarco stimò che l’angolo al momento della metà dell’illuminazione era di 87 °, quindi il rapporto tra le distanze è sin 3 °. Naturalmente, abbiamo tradotto questo concetto in notazione moderna perché Aristarco non usava i gradi, né era stata inventata la trigonometria, quindi non aveva la funzione seno a sua disposizione. Tuttavia questo è in effetti il ​​calcolo che ha effettuato, corretto in linea di principio ma quasi impossibile da osservare in pratica poiché determinare il momento in cui si verifica la metà dell’illuminazione della luna può essere trovato solo in modo molto impreciso.Aristarco si trovò quindi a calcolare un’approssimazione per ciò che è nella nostra notazione sin 3 °. Ha ottenuto la disuguaglianza 1 / 18 > sin 3 °> 1 / 20 e dedusse che il sole era tra le 18 e le 20 volte più lontano della luna. Infatti al momento della metà dell’illuminazione l’angolo tra la luna e il sole è in realtà di 89 ° 50 ‘e il sole è in realtà circa 400 volte più lontano della luna.
Piuttosto stranamente Aristarco usa i valori per l’angolo sotteso dal sole e dalla luna per essere 2 °. Questa cifra è abbastanza imprecisa in quanto è quattro volte troppo grande. Usa correttamente l’evidenza delle eclissi per affermare che il sole e la luna sottendono la stessa angolazione. Tuttavia, Archimede cita un valore di 1 / 2 ° per l’angolo sotteso dal sole e attribuisce questa cifra a Aristarco. Possiamo solo supporre che Aristarco abbia scritto Sulle dimensioni e le distanze del Sole e della LunaAll’inizio della sua carriera, in seguito adottò la sua ipotesi di un universo centrato al sole e calcolò un valore molto più accurato dell’angolo sotteso dal sole. Si deve presumere che Aristarco sia stato in grado di sviluppare strumenti per effettuare misurazioni astronomiche accurate più avanti nella sua carriera.Neugebauer sostiene in [ 6 ] che Aristarco non era interessato a dati astronomici accurati (poiché avrebbe potuto facilmente fare molto meglio se fosse stato interessato). Piuttosto Neugebauer suggerisce, Aristarco era interessato solo alla teoria matematica alla ricerca delle distanze e dei diametri. Stava dimostrando che tali misurazioni potevano essere fatte e, dal momento che riesce a dimostrarlo, il suo lavoro è di grande importanza. Come scrive Neugebauer in [ 6 ]: -… il potere dell’approccio matematico ai problemi astronomici è stato drasticamente dimostrato, nello stesso senso in cui Eudosso , un secolo prima, costruiva modelli cinematografici che potevano essere collegati ai moti planetari senza risolvere un singolo problema specifico.
Ci sono uno o due altri riferimenti al lavoro di Aristarco che sono stati indagati di recente. Ad esempio in [ 7 ] gli autori interpretano: -… un passaggio difficile in un commento anonimo scritto in greco nel corso del 2 ° secolo dC su Book 20 di Omero Odissea ‘s. … l’ autore [ anonimo ] cita Aristarco di Samo citando Talete ed Eraclito per sostenere la sua tesi [ di ] eclissi solari … [ La sua ] tesi riguardante i tempi in cui si possono verificare eclissi solari si basa su un’analisi di greco ed egiziano convenzioni di calendario, piuttosto che un appello all’osservazione delle eclissi solari.

La struttura del sistema solare

Il passaggio da una visione del sistema solare centrata sulla Terra (geocentrica) a una centrata sul Sole (eliocentrica) dura oltre 2000 anni. La prima proposta nota di una visione eliocentrica proviene dall’astronomo greco Aristarco nel 280 aC circa. Sotto l’influenza di Pitagora , Aristotele e Platone , uno dei principali obiettivi dell’astronomia della Grecia antica era sviluppare un modello geometrico dell’universo che consentisse loro di prevedere i movimenti dei corpi celesti. Per motivi filosofici, poiché i cerchi erano associati alla perfezione e anche i cieli o i “pianeti” erano considerati perfetti e immutabili, era importante che i movimenti di tale modello fossero circolari e uniformi. Il primo tentativo di un tale modello è stato Eudosso che usava un sistema di sfere concentriche con la Terra al centro. Altri modelli furono sviluppati da Apollonio, Ipparco e Tolomeo che introdussero rispettivamente epicicli, eccentrici e e quanti per aumentare l’accuratezza della predizione.Durante la caduta di Roma nel IV e V secolo e nell’alto Medioevo (secoli dal VI al X secolo), il progresso astronomico era scarso in Europa. C’erano solo alcune eccezioni degne di nota come Martianus Capella di Cartagine. In contrasto con il sistema tolemaico in cui tutti i “pianeti” orbitavano sulla Terra, Martianus propose che Mercurio e Venere orbitassero il Sole, con il Sole che orbita attorno alla Terra. Il suo lavoro fu in seguito riferito da Copernico .Mentre i progressi in Europa sono lenti, l’astronomia islamica è fiorita. Un centro di traduzione conosciuto come la Casa della Saggezza fu fondato a Baghdad. Ciò ha permesso che le opere astronomiche di una serie di tradizioni come l’astronomia greca e indiana fossero assimilate al pensiero islamico (importanti astronomi indiani includono Aryabhata , Varahamihira e Brahmagupta ). Nei secoli a venire sorsero dibattiti sulla validità del modello tolemaico con astronomi come Thabit ibn Qurra che disegnavano incoerenze tra il modello geometrico di Tolomeo del sistema solare e la sua visione fisica di esso. D’altra parte al-Battani rispettò molto il modello tolemaico e lo modificò migliorando il trattamento del modello dell’orbita del Sole intorno alla Terra. Il suo lavoro è stato citato almeno ventitré volte in Copernico ‘s De revolutionibus pubblicato nel 1543.In questo lavoro, Copernico puntava a un modello più elegante, che disponesse degli equipe tolemaici. Ciò ha attirato un fervido sostegno da parte di Galileo . Tuttavia, per ottenere qualcosa di simile alla precisione, Copernico dovette mettere il sole un po ‘lontano dal centro dell’universo, e usare ancora più epicicli di Tolomeo , il che complicò il modello. Altri astronomi come Brahe e al-Battani avevano sviluppato modelli geocentrici che davano previsioni più accurate rispetto alla visione copernicana, che quindi non riuscì a prendere piede. Kepler poi fatto un anticipo rivoluzionario. Ha postulato che le orbite planetarie fossero ellittiche anziché circolari, andando contro la visione secolare di coloro che erano influenzati dalla filosofia greca. Usando questa ipotesi, fu in grado di predire il transito di Mercurio attraverso la faccia del Sole, per la prima volta nella storia umana. Tuttavia, 50 anni sul principale astronomo del giorno Cassini aveva ancora una visione geocentrica come proposto da Brahe . Fu solo quando Newton usò le leggi di Keplero come prova della sua legge di gravitazione universale nei Principia che il modello eliocentrico iniziò veramente a guadagnare terreno. Tuttavia, rimanevano problemi come la mancanza della parallasse osservata.

Referenze

1. WH Stahl, Biografia nel dizionario della biografia scientifica (New York 1970-1990).
   http://www.encyclopedia.com/topic/Aristarchus_of_Samos.aspx
2. http://www.nndb.com/people/756/000096468/

Libri:

1. TL Heath, Aristarchus of Samos (Oxford, 1913).
2. TL Heath, Aristarchus of Samos. L’antico Copernico : ristampa dell’originale del 1913 (New York, 1981).
3. TL Heath, Una storia di matematica greca I, II (Oxford, 1931).
4. O Neugebauer, A History of Ancient Mathematical Astronomy (3 Vols.) (Berlino-Heidelberg-New York, 1975).

Articoli:

1. AC Bowen e BR Goldstein, Aristarchus, Thales ed Eraclito sulle eclissi solari: un commento astronomico su P Oxy 53.3710 cols. 2.33-3.19, Physis Riv. Internaz. Storia Sci. (NS) 31 (3) (1994), 689-729.
2. M Gabriel, Le teorie heliocentriques dans l’antiquite grecque, Ciel et terre: bollettino della Sociége belge d’astronomie et revue populaire d’astronomie, de meteorologie et de physique du globe 104(1988), 107-108.
3. O Gingerich, Copernico ha un debito con Aristarco ?, J. Hist. Astronom. 16 (1) (1985), 37-42.
4. M Milankovitch, Aristarchos und Apollonios. Das heliozentrische und das geozentrische Weltsystem des klassischen Altertums, Acad. Serbe Sci. Publ. Inst. Matematica. 9 (1956), 79-92.
5. O Neugebauer, Archimede e Aristarchus, Isis 34 (1942), 4-6.
6. R von Erhardt ed E von Erhardt-Siebold, Sand-Reckoner di Archimede. Aristarco e Copernico, Iside 33 (1942), 578-602.
7. BE Wall, Anatomy of a precursor: la storiografia di Aristarchos of Samos, Studies in Hist. e Philos. Sci. 6 (3) (1975), 201-228.
8. SV Zhitomirskii, L’ipotesi eliocentrica di Aristarco di Samo e antica cosmologia (russo), Istor.-Astronom. Issled. No. 18 (1986), 151-160.