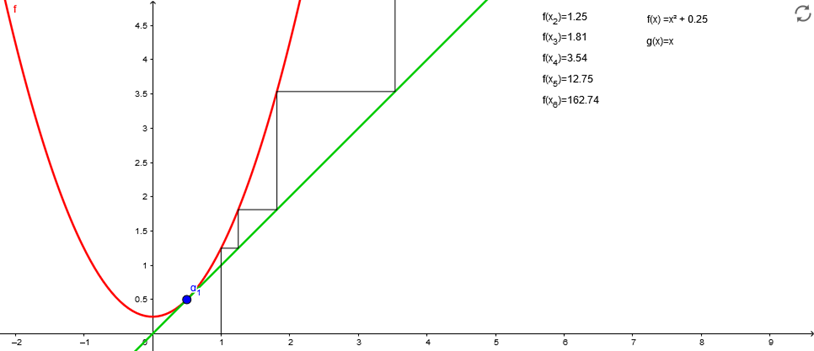
Verhulst Diagramm - Spinnwebdiagramm
Das Verhulst Diagramm wurde nach dem belgischen Mathematiker Pierre-François Verhulst (1804-1849) benannt.
Es ist eine graphische Möglichkeit Funktionen zu iterieren. Ein Vorteil, den das Diagramm bietet ist, dass man sehr schnell erkennen kann, ob eine Folge gegen unendlich divergiert oder zu einem Fixpunkt konvergiert oder unter iteration einen chaotischen oder periodischen Orbit einschlägt.
Funktionsweise
In einem Koordinatensystem zeichnet man die Identitätsgerade f(x)=x und die zu iterierende Funktion.
Der Startwert ist der Startpunkt auf der X-Achse.
Von hier geht man parralel zur Y-Achse auf den zu iterierenden Graphen.
Anschließend parallel zur X-Achse auf die Identitätsgerade. Die Stelle, an der die Parallele auf die Identitätsgerade trifft (der X-Wert) ist der Wert, den man nach einer Iteration erhält. nun kann dieser Vorgang auf die selbe Weise wiederholt werden. Wenn man die Parallelen einzeichnet, lässt sich der Orbit schön nachvollziehen und nach ein paar Iterationen relativ gut vorraussagen, was als nächster Wert ungefähr rausgeht, es sei denn es liegt eine chaotische Dynamik vor.
Natürlich kann man damit auch rekursive Folgen darstellen. Dass man diese meist in eine iterative Folge/Form umschreiben kann haben wir uns schon im Post Fraktale I - Iteration angeschaut.
Außerdem gibt es einem die Möglichkeit Funktionen einfach zu verketten.
Dafür trägt man einfach die zu verkettenden Funktionen alle in das Koordinatensystem ein und geht mit den Y-Achsen-Parallelen in Verkettungsreihenfolge auf die jeweiligen Funktionen.
Viel Spaß mit dem Diagramm.