Marine Paradox

Marine Paradox is a weird geometric problem. Let's start with the Australian coastline range. The Australian coastline has been given 36,735 kilometers in the year book of Australia, published in 1978. In the Australia Handbook book, on the other hand, this limit is mentioned 19,320 kilometers. Obviously it is understood that the second case is about half of the first of the range!
When we measure anything, due to different types of measurable limitations, the measurements are a little bit nimble, but it does not turn out to be doubly or half at all. So why are you facing this problem while deciding the maritime boundary? The reason for this is the fractal dimension in mathematics. The above two segments of Australian seafront mentioned above are quite apparent in their respective areas, but their values are quite different. For this reason, a paradox is formed when measuring the maritime boundary (Paradox has been discussed in a previous article). This paradox in math is known as the coastline paradox or maritime paradox.
For better understanding of this issue and to apply mathematics to the subject better we can give "Koch snow flake". Helg Von Koch thought of a kind of geometric shape similar to a snowflake, each of which could be divided into a more narrow arm. For example, we can start with a triangle (first image). By dividing each arm of the triangle into the ratio of the primary triangle, we get a snowflake picture. In the same way, we can divide each arm of this snow particle into a smaller arm. In this way, if we continue to divide each arm, it is possible to carry it to infinite. And in mathematical terms, each step is called each iteration. For example: if we take seven primaries in our primary triangle, then each sequence of images will be sequenced by the following:
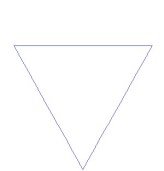




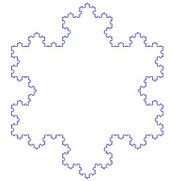

The difference is not easily understood at the end, because the braces of the arms are quite precise. In this way, if we divide the arms of a field, then the area of each increment will increase the range of one third of the previous step. If we continue to do this thing infinitely, we will find a finite field with an infinite range. How do we understand that the field will be finite? We can easily fill the limited area with a pencil. But if we continue to trace the field's range through a pencil then I can not even finish it because it is infinite. As much as we try to magnify this line, we will see that it is divided into more subtle divisions.
But do not go to the infinite, let's find out the range for a specific erection:
If the number of iteration is n, then because the number of arms is four times the per-inch, so the total number of arm will be,
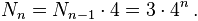
Again, if the length of each side of the primary triangle is s, then after the erection, each arm will be of length,
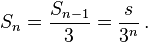
So there will be a total range,
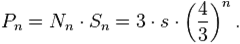
From here, our maritime paradox can be reached. The cochlear snowflake is an example of a fractal (the simple fact is that the fractal is the geometrical shape that happens to be revived if the pattern is magnified). In the same way, in our real world, the world or the territories are like fractals. For example, we can draw the map of Bangladesh with various dimensions.
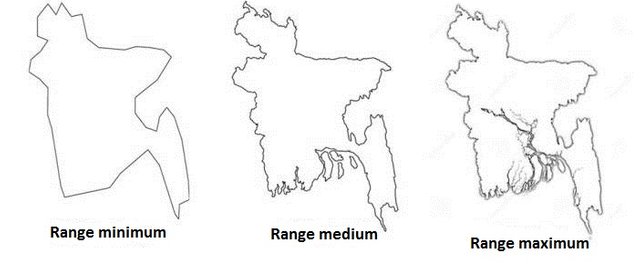
If you want to make this map so sophisticated, we can move to the atomic stage. And for the same reason we can carry a range of countries according to the precision of its details, to the extent that it can be infinite.
In 1967, with the limitations of seismic limitations, mathematician Benois Mandelbrott was quoted in the Royal Journal of Science as "How Long Is the Coast of Britain?" Statistical Self-Similarity and Fractional Dimension "published a paper. There he highlighted the problem of determining Britain's demarcation boundary. He said that the extent of the maritime boundary of a country will depend on how much we will measure with the length of the timber. If we measure Britain's maritime boundary with a width of 50 kilometers, then its limit will be 3400 kilometers. And if you measure with a length of 200 kilometers long then you can get 2400 kilometers. The smaller we take the length of the wood, we can calculate the size of the more narrow and minor turns (see the picture below) and therefore the amount of sea level will increase.
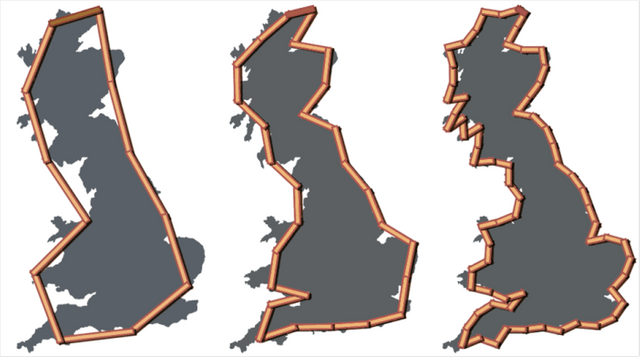
What is the way to get rid of this problem? Can we not count the maritime boundaries? The answer is: No, there is no way. However, an indirect arrangement can be taken to determine the marine boundary, and if we measure all the boundaries with the same fixed stick and specify the length of the timber, then there will be a comparable value in each range measurement. Although we can not find the exact range in this method, we will get ideas of how big or small the range is.
Congratulations @rubai18! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP@OriginalWorks
The @OriginalWorks bot has determined this post by @rubai18 to be original material and upvoted it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
To nominate this post for the daily RESTEEM contest, upvote this comment! The user with the most upvotes on their @OriginalWorks comment will win!
For more information, Click Here!
thats great
thanks for your feedback
i am upvoted and reply your post plz visit me
upvoted,reply,follow and resteem when you work in steemit thanks alot,
my id = https://steemit.com/@pranashroy
thanks for visit my profile. i also visit your post
This is really interesting! I liked your post.
May I give you a tip on how to gain in your posts credibility? It's a good idea to name your sources and credit your images. Even if what you say is common knowledge or things taught in schools, the science tag needs the credentials.
thanks for your feedback.
I love science. Science is very interesting to me
I can see from your past posts! That's why I left such a comment.
Steem on and keep smiling! :)