A Long Awaited Proof
“Archimedes will be remembered when Aeschylus is forgotten, because languages die and mathematical ideas do not. “Immortality” may be a silly word, but probably a mathematician has the best chance of whatever it may mean.” --G.H Hardy
Has it ever happened with you that you were sitting in the same place for hours and thinking about some puzzles of physics and mathematics? Well, it happened with me. Now think about a single problem in math, a theory which has been making every mathematician’s hair grey for two hundred years. Yes, you spelled it right two hundred years. The man who invented this theorem, he claimed that he invented the proof and he lost it and he never wrote it down again anywhere. Well, my friends, to prove the theorem mathematicians tried for last two hundred years. The name of the theorem is Fermat’s Last Theorem. It was invented by Pierre de Fermat which says exactly that if x, y, z are three integers there is no number n>2 which satisfy the equation: x^n +y^n = z^n. 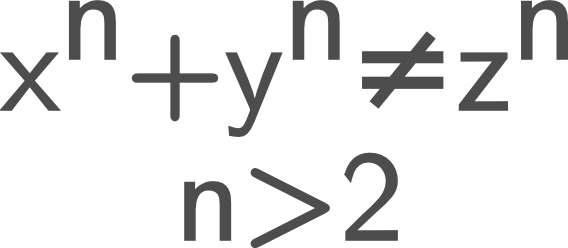
Fermat's last theorem | source
For example if power two of number two added with power two of number three is twenty- five, where value for n is 2. And if we do five squared, it will give us 25. There are a lot numbers which satisfy the equation for n equals two. But when n is greater than two there is not such three numbers which will satisfy this equation.
Fermat's theorem for n=2 | source
Now you would say we don’t need Fermat to say that, we all know this from intuition. But my friends there are a infinite amount of numbers in the real axis. You and I don’t know all of them and there is no value of any ideas or theorems in mathematics and physics if you can’t prove it. Fermat’s last theorem was without proof for two hundred years. Although this theorem is given by Fermat, it has its origin in ancient Greece and directly linked to the great theorem of Pythagoras. I think everyone is familiar to this theorem. But let me remind you another time. It says that— In a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
Pythagoras Theorem | source
I still remember when I was at second grade of high school math professor used to force us to memorize this theorem because in every exam, when you see the question paper, you can always find Pythagoras theorem. Every student in high school knows this theorem. But wait, here is the twist. This theorem created another theorem which was given by Fermat, made mathematicians crazy nights after night.
History of Pythagoras and his theorem
Pythagoras of Samos was one of the greatest minds mathematics has ever produced. He developed mathematical logics which brought the first golden age of mathematics. He made numbers greater than something they used to be. He is the first person who just didn’t use number only for counting rather he believed in it as a profound language which can explain thing from a deeper sense, in spite of anyone’s opinion or prejudice. That is much more absolute than any knowledge existed before. He worked with certain types of numbers, relations between them as well as the pattern they can form. He gained his mathematical knowledge travelling around the known world back then. He traveled to Egypt and Babylon who were much more advanced than their time. These people not only used mathematics for counting, they were using mathematics for complex calculations for creating so precise accounting systems and to construct complex buildings and architectures. They saw mathematics as a tool for solving applied problems. The motivation of Egyptians was just to count the boundary of lost land because of every year's flood. They were satisfied that the rules or theorems work. But they didn’t ask why they work?

portrait of Pythagoras|source
The tale goes like this, he travelled for twenty years and gathered all knowledge he had learnt and set sail for his motherland Samos with an ambition to establish an academy to teach students what he learnt and to invent new mathematical ideas. He used to pay his students three cent for each lesson. Then he noticed that as weeks were passing by, the intention to earn money has changed into a thirst for knowledge. Then he said them that he would not be able to hold the classes, cause he could no more able to afford to teach the students and pay them. Then the students started to pay him.
Pythagoras soon became famous all over Greece. He had around six hundred followers, who devoted themselves to learn and invent new theories and to construct their proofs. Besides Pythagoras theorem there are a lot of important mathematical ideas which came from Pythagoras and his followers. One of them is perfect number. As Pythagoras said a number's perfection depends on its divisors. If we divide the original number by some numbers and get the result as a whole number, then these numbers are called divisors. For example the divisors of number 6 are 1, 2 and 3. When the sum of the divisors of a number is greater than the number itself then the number is called an excessive number. For example divisors of number twelve is 1, 2, 3, 4, 6. If we add them up (1+2+3+4+6 =16) we get 16, which is bigger than the number 12. So, 12 is an excessive number. There is numbers if we add its divisors up, the result is less than the original number. For example, 10 is this kind of number. This kind of numbers are called defective numbers. But there are numbers if we add up its divisors, we get exactly the same number. They are called the perfect numbers. For example 6 has divisor 1, 2, 3. Their sum is exactly 6. So 6 is a perfect number.

Perfect number | source
But the most important theorem is Pythagoras theorem. This theorem defines right angles. It shows us if we know the two small sides of the right angle, we can easily measure the other side which has its application in almost every area of mathematics.
The missing proof
Fermat’s last theorem revolves around the search for a missing proof. The idea of proof in mathematics is much more profound and powerful than our day to day life. If something is proven in mathematics it is absolute and true until the end of time. In mathematics certain axioms are thought to be true and they are the most fundamental logic. Arguing logically and step by step one can come to the conclusion which is the theorem itself. If the methods and steps are flawless, the theorem is proven and it is true until the end of time. In physics and chemistry it is different. First we put forward a hypothesis to explain a physical phenomenon. Then we try to find evidence for the favor of the hypothesis and try to explain other theories. Then we can think of it as a law. But it doesn’t need to be absolute until the end of time. They are always an approximation. For example Newton’s law of gravity which was true for 300 years until Einstein showed it is wrong or just an approximation of theory of relativity.
This is a story of a young boy named Andrew Wiles. He used to go to the public library on his way back from school to home. One day in library, he discovered one book by E.T. Bell titled ‘The Last Problem’. There he started reading about Pythagoras and his theorem, his life in Samos and development of theorem. But this book also talked about another sister equation where the three numbers in Pythagoras theorem is squared, in this equation they are cubed. That means in this equation the power of x, y, z is no longer 2, but it is 3. Finding three numbers that can fit the cubed equation seemed to be an impossible job. It appeared to be an impossible job. There appeared no number which can satisfy the equation.
Fermat was one of the most brilliant minds in the history of mathematics. It was impossible for him to check infinity of numbers. But he was absolutely sure no such three whole numbers exist because his claim was based on proof. But no such proof has been ever discovered. Even Euler made Fermat's house searched, but there was no existence of such proofs. The book ends up without a proof. This made Andrew Wiles determined which has made him a mathematician and he spend his whole life trying to prove the theorem.

Andrew Wiles |source
The Proof
In 1993 the young kid Andrew Wiles, who was then a professor of Princeton University announced that he has proven the last Fermat theorem. This kind of claim was not rare for the past three centuries. But this time was different. He came to hold a lecture in Cambridge. All the respected mathematicians came to attend the lecture. So, Wiles started. Blackboard after blackboard was filled with calculations. Step by step, the proof started becoming clear to the audience. In the end he finished the lecture. The long road of proving Fermat’s theorem is over. Wiles had done it. He won the prestigious "Abel Prize". Finally mathematicians have won their war of three centuries.
I appreciate the effort you put into writing this. You have earned my upvote. :)
Thank you so much @maticpecovnik. I appreciate it .
thank you @justtryme
Congratulations @rifkan! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @rifkan! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP