Where do conservation laws come from and how does nature enforce them?

We explore these question by examining one particular conservation law, the conservation of electric charge. Electric charge can flow from place to place, but a net electric charge can be neither created nor destroyed. Maxwell’s electromagnetic equations and the geometry of space-time imply the conservation of charge by governing how information about charge is communicated to the rest of the universe.

What is the nature of the laws of physics? How do they work? How are they enforced? We explore these questions using conservation of electric charge as our example.

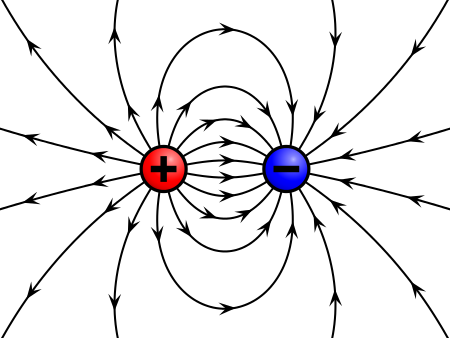
Particles can have positive, negative, or zero charge. These particles can move around, be created, or be destroyed, but their charge is always conserved. Imagine a limited region of space-time where we could create or destroy charge. Could we use such a time span to create a net electric charge? Surprisingly, we could not. Charges could be made or destroyed during the period when the laws did not apply, but when the span ends, the charge must end up at zero. If we turn off a conservation law, it is still enforced. The answer how is one of the most remarkable ideas in all of physics.

James Clerk Maxwell’s electromagnetic equations tell us how electric and magnetic fields are related to charges and each other.

A field is what physicists call a region of space-time affected by a particular force. A wind map is a useful analogy. The wind may be fast or slow, headed north or south at any given point, but every point on the map has a particular wind speed and direction. At each point in space-time, the electromagnetic field has a direction (push) and a strength (flux). Keep in mind, however, that nothing is actually flowing through the field.

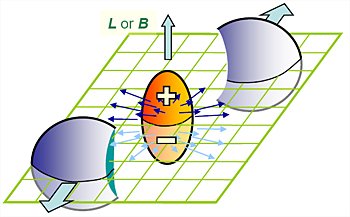
Now, instead of a map, picture a hollow cube.

Each side of the cube is a square with a positive side and a negative side. All of the positive sides point outward. The edges of square are positive at one end and negative at the other, in a counterclockwise direction. Flux, in this case, is the flow of wind through a side of the cube. We can call this → FW. We say → FW is positive when the wind flows from the negative to the positive side, negative when it flows from the positive to the negative side, and zero when the wind runs parallel to the side.

Could → FW be positive through all 6 sides at once? Yes, if the wind source is in the center. Push is the wind moving along the edge of a side. → PW is positive when it moves from the negative to the positive end of the line, negative when it moves from the positive to the negative end, and zero when it is perpendicular to the line. We have positive net I. → PW when the wind shears counterclockwise around a side.

How does this image apply to electromagnetism?

The basic laws of electromagnetism are defined by Maxwell’s equations, all 4 of which can be explained in terms of the flux and push of the fields.

The first equation, Gauss’s law (named for Karl Friedrich Gauss) defines charge (q) in terms of the flux of the electrical field: → FE = q.

Returning to our box, if q is positive, field lines flow out of the box. If q is negative, they flow into the box.

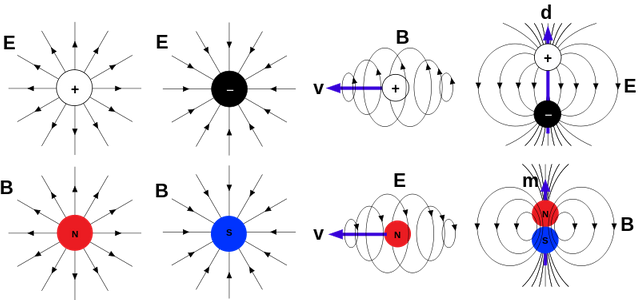
The second equation, Gauss’s law for magnetic fields, is similar: The magnetic fl ux, → FB, is always zero. A magnet always has a positive and a negative end.

There are no monopoles; nothing is all magnetically positive or negative. The field lines form closed loops or stretch forever.

The third and fourth laws deal with the rate of change of x over time (˙ x). For the third equation, Faraday’s law (named for Michael Faraday), we return to our cube.

In this situation, → FB is the flux through one side of the cube. This is not necessarily zero, because we are not concerned with the whole cube. The net electric push around the outside edge of this side of the cube is → PE. According to the law, → PE = −→ F ˙ B This is the law that allows a magnet moving rapidly near a wire coil to generate an electric current.

In the fourth law, Ampère’s law (named for André-Marie Ampère), → PB (the net magnetic push around the outside of the square) is equal to I (the electric current through the square in the positive direction).

This law is what makes electromagnets work. All of these electromagnetic equations were known before Maxwell came along. His brilliant insight was to realize how they fit together.

Maxwell and his successors derived all sorts of amazing things from the laws.

• Changing magnetic fields can produce electrical fields.
• Changing electrical fields can produce magnetic fields.
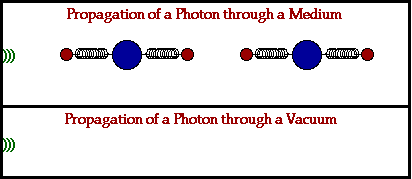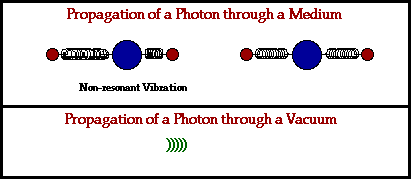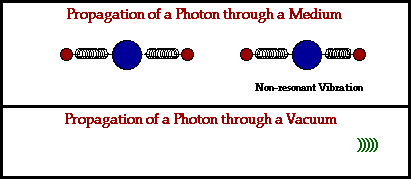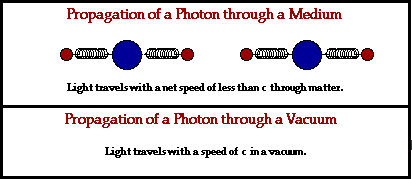
• Disturbances in electric and magnetic fields can propagate through empty space as electromagnetic waves.
• Light is an electromagnetic wave.

How does all this prove that we cannot violate the conservation of charge?

Imagine again a box where we could suspend the conservation of charge for a limited period of time say, one day. At the start of the day, q = 0. No changes cross the walls in either direction all day, so I = 0 for the 6 sides of the box. While the laws do not apply inside the box, they are still working outside the box and in the walls of the box. If we apply Ampère’s law to each side of the cube, the sum of all the currents of all the sides is zero. No matter what is going on inside the box, the net electric flux through the box does not change its rate of change is zero. At the end of the day, when the laws go back into effect, Gauss’s law for electric fields applies again, so q = 0.

No matter what happens inside the box during the day, there can be no net charge in the box at the end.

The field outside the box still enforces conservation of electric charge. If new charge appears inside the box, it affects the entire electric field, even very far away. The information about the new charge travels as a disturbance, or wave, in the electric and magnetic field. Maxwell’s equations say only transverse waves, perpendicular to the field, can travel in the field. But this information requires a longitudinal wave, parallel to the fi eld, to travel. The outside field thus cannot carry the news of the new charge in the box; conservation of charge censors the information, preventing its spread to the rest of the universe.

Do other conservation laws work this way?

For energy, conservation is enforced by gravitational fields. Conservation of baryon number is not enforced by any field, but baryon number may not be exactly conserved in cases like sphalerons. Consider empty space in which there are no electric charges or currents. Maxwell’s equations in empty space show that there is a symmetry between electric and magnetic fields in the equations.

---

---

or @pjheinz

---

Image Credits: 1, 2, 3, 4, 5, 6, 7, 8

---