Quantum World Inspires To Develop a New Realm Of Mathematics
In our minds, mathematics seems to always carry a noble temperament, it is followed by some eternal truths. However, in fact, the development of mathematics is also a result of the trend-setting, and many of the origins of mathematical concepts are related to the experience of daily life. For example, the development of astrology and architecture inspired the study of geometry by ancient Egyptians and ancient Babylonians; in the scientific revolution of the 17th century, the development of mechanics brought calculus.

In order to fully understand quantum physics, mankind needs to open up new mathematical boundaries.--source
Among the quantum theory, although elementary particles have nothing to do with our daily experience, the friendship between physics and mathematics is particularly eager here. There are many strange phenomena in the quantum world, such as an object can exist in two different places at the same time, its evolution follows the rules of probability. Compared with the classical physics, these counter-intuitive features are actually closer to the nature of nature, but also provide a broad platform for the development of modern mathematics. So we can not help but reverie, once we fully understand and accept the quantum theory, then the inherent logical structure of quantum theory is it possible to open a new field of "quantum mathematics"?
The intimacy between mathematics and physics has a long history. Galileo once said: "The universe is a masterpiece of great master, recorded all the knowledge and wisdom, ready for human beings to read .However, only by understanding the book of the text, can understand its esoteric significance, and this masterpiece is precisely with Written in the language of mathematics.
Feynman also said:" If one does not understand mathematics, it is hard to understand the beauty of nature at its deepest level ... If you want to know nature, enjoy Her beauty, she must speak her language. "(Feynman also said" If mathematics suddenly disappears, then physics will go back a full week. "In this regard, a mathematician explains: This is the week of God's creation. ")
source
Mathematical physicist and Nobel laureate Eugene Wigner once praised the amazing ability of mathematics to describe the objective world. "The validity of its application to the natural sciences is simply 'unscientific,' and the same mathematical concept can be applied Among a number of different specific research questions. However, as quantum theory begins to play an incalculable impetus in modern mathematical research, we are witnessing a reversal of the situation.
The concepts of particle physics, especially the string theory, seem to have a peculiar correlation with a large number of different areas of mathematical research. Regardless of whether or not the string theory can eventually gain a firm foothold in the physics system, it has far-reaching implications for mathematics. It has some far-reaching implications in terms of analysis, geometry, algebra, topology, representation theory, combinatorics, and probability theory The dazzling math field has a connection. Think of mathematics students to learn so many things, can not help but feel bad for them for 1 second.
So, quantum theory is so useful for mathematics, whether there are any underlying reasons? In the a precise view, this may be another perverse feature of the quantum world: all that can happen does happen.
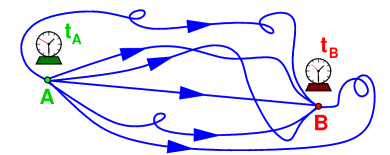
In simple terms, what classical mechanics does is calculate how a particle moves from point A to point B. For example, the actual motion trajectory may be a geodesic, the shortest curve connecting two points on a surface. In quantum mechanics, we need to take all the possible paths from A to B into account, and even include the same entangled paths as headphone lines. This is Feynman's famous "historical summation."
According to the laws of physics, every possible path has a certain weight, representing the probability of its possible occurrence. The result given by the classical Newtonian law of motion is precisely the one with the highest probability of all paths. Therefore, quantum physics treats all paths as a weighted ensemble, allowing us to take all possibilities into account by summing up.
"Historical summing up" is actually a kind of global thinking that deals with all possible situations in one go. This coincided with the spirit of modern mathematics, such as mathematicians in the study of the object "class", more attention is the relationship between objects rather than a single object. It is the overall view of this high-rise construction of quantum theory that leads to another marriage between mathematics and physics.
Quantum calculator
Taking the "Mirror Symmetry" in the string theory as an example, it involves the peculiar equivalence between different spaces. It not only brings about geometric revolution but also fully reflects the magic power of quantum physics. The story begins with an enumerative geometry - a well-developed branch of algebraic geometry that counts the number of solutions to a geometric problem.
In chord theory, the space-time dimension may be ten or more, and we can hide additional space-time dimensions with six-dimensional Calabi-Yau spaces. If we apply Einstein's gravity equation to a six-dimensional card-mound space, then the geometric solution will be a curve in six-dimensional space. What we care about now is how to count the number of these curves?
source
In three-dimensional space, we can circle a rope around many circles in the cylinder. In the card-hill space, there is also a parameter called "degree", which is an integer and is used to describe the curve degree. Calculating the number of curves for a certain degree of difficulty is very difficult, even in the simplest card-mound space - the so-called quintic.
As early as the 19th century, mathematicians calculated by the classical method, a total of 2875 kinds of 1 degree curve; 2 degree curve results were calculated before and after 1980, a total of 609,250 kinds; and to calculate the number of 3 degree curve, it can only Involved in the string theory scientists.
source
Around 1990, a string theory team of scientists asked the geometer to calculate the number of 3-degree curves. The geometry programmer wrote complex computer programs and ended up with a result, but the string theorists felt there was a problem with this result, possibly because of a mistake in the code. After careful examination, the final confirmation of the code is indeed wrong - but how do string theoreticians know?
In fact, string theorists have been trying to translate this geometric problem into a physical one. In the process, they have developed a set of methods that can calculate the number of all degree curves at once. As soon as the result came out, the math circle exploded. It's like finding a way to climb all the mountains at the same time, no matter how tall the peaks are.
In quantum theory, the fusion of the numbers of all degree curves into a single function is a natural grace with a definite physical meaning. We can think of this function as the probability of a string spreading in a card-mound space and applying the principle of "historical summation." As the chord moves all the possible curves simultaneously, all possible degrees are involved, so it is an extremely efficient "quantum calculator."
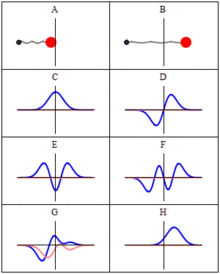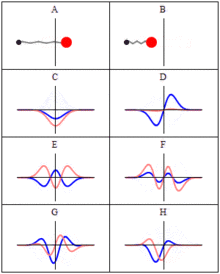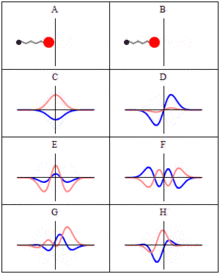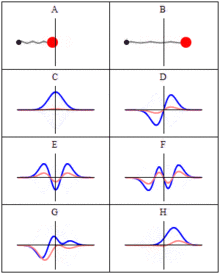
Comparison of classical and quantum harmonic oscillator conceptions for a single spinless particle--source
However, in order to find a concrete solution, but also need to use "mirror" card - mound space. The real mirror can present a completely symmetrical image with the real world. The mirror card-mound space is not so simple: the shape of the mirror space is quite different from that of the original space, and even the topological structure is different. But in the quantum field, there are many similarities between them, and the chord in which we are concerned is exactly the same. Therefore, complex calculations in the original space can be greatly simplified in the image space, only one point can be completed. Get it!
Duality: Both ends of the balance
Mirror symmetry interprets one of the salient features of quantum physics, duality: two different classic models that, if placed within a quantum framework, are actually equivalent, as if magic was applied, The difference suddenly disappeared. The existence of duality indicates that quantum physics has some profound and covert symmetry. Often, our understanding of duality is very limited, which means that the current quantum theory is far from perfect.
The earliest and most famous example, was a "wave duality." Wave-particle duality means that for any quantum object, such as an electron, we can think of it as a particle, or as a wave. Two perspectives have their own advantages, to provide different ways of understanding the same physical phenomenon. Whether we should treat electrons as particles or waves depends not on the nature of the electrons themselves, but on the way we ask questions. Similarly, mirror symmetry in chord theory provides two equivalent and effective perspectives for Quantum Geometry.
Mathematics has the wonderful ability to connect different worlds. In any formula, the most overlooked part is the low-key but indispensable "equal sign." The equal sign is like the flash of light in your mind that communicates the wisdom on either side of the equation. Einstein is definitely an expert in the use of equal signs. He proposed the mass energy equation E = mc2, undoubtedly the most famous equation in human history, no matter how elegant its praise is not an exaggeration. This equation states that mass and energy, both of which are independent of physical concepts before the special theory of relativity, are in fact completely equivalent; that mass can be transformed into energy, and that energy can be transformed into mass.
Later, Einstein further established the general theory of relativity, which may not be as eye-catching and famous as the former, but it links geometry and matter together, the result is equally amazing. In simple terms, the general relativity equation shows that matter affects the bending of space-time, while space-time affects the movement of matter.
Mirror symmetry is another great example of the power of an equal sign. It connects two different mathematical worlds: one is symplectic geometry, which is a branch of mathematics that forms the basis of mechanics; the other is algebraic geometry that involves plurals. Quantum physics now communicates these two fields of mathematics, unexpectedly leading to a "grand unification" of mathematics.
It is indeed gratifying to have such a close relationship between disciplines. The development of mathematics is benefiting from quantum physics and string theory, and the rough physical intuition is transformed into rigorous propositions and proofs. At present, mathematicians are close to concluding a rigorous proof of homological mirror symmetry, a substantial expansion of the original theory of mirror symmetry in string theory.
For example, this is equivalent to compiling a transliteration dictionary for the relationship between all objects and objects in the two math worlds. Of course, these maths prove that they tend not to follow the idea of physical reasoning (mathematicians may not wipe out physicists!) Instead, they need to find new ways to prove. This further shows that there is some deep and still unknown internal logic between quantum theory and objective reality.
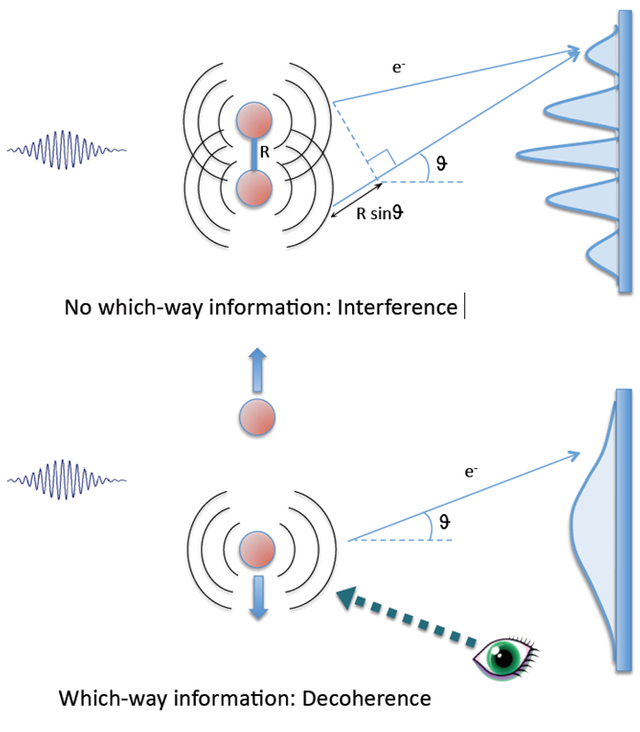
Top panel: Molecular version of Young’s double-slit experiment
Bottom panel: Molecular version of Einstein-Bohr gedanken experiment--source
"Complementarity" is an important principle in quantum mechanics, and the Copenhagen school led by Bohr is a faithful fan of this concept. In quantum mechanics, using the Heisenberg uncertainty principle, it can be shown that it is impossible for any system to have both a fixed momentum and a definite position coordinate.
On 19 October 1926, Pauli concisely wrote in a letter to Heisenberg: "It seems as though we have two eyes, one observing the momentum and the other one observing the position coordinates , But it would be schizophrenic if we both opened our eyes at the same time. "Based on this uncertainty, Bohr proposed the principle of complementarity: Momentum reflects some of the features of the physical system and the position coordinates reflect.
Other features of the physical system are complementary to each other; however, we can not know all the features of the system at the same time. The exact result we get depends on how we observe it.
In his later years, Bohr endeavored to promote the principle of complementarity to a more general philosophical proposition. His favorite complementary relationship was "truthfulness" and "clarity."
Perhaps the rigorous and physical instincts of mathematics can also constitute a complementary pair in scientific research. We can look at the world with mathematical eyes and physical eyes, but for now, we do not have the courage to open both eyes.

References for Text and Images:
Support @steemstem and the #steemstem
project - curating and supporting quality STEM
related content on Steemit

helpful topic
just checking the topic like this
good work
if you think about it Quantum programming is just a step away from blockchain tech....informative 😎 likes and followed!
This post has received a 0.77% upvote from thanks to: @marverick984.
thanks to: @marverick984.
For more information, click here!!!!
Send minimum 0.010 SBD|STEEM to bid for votes.
Do you know, you can also earn daily passive income simply by delegating your Steem Power to @minnowhelper by clicking following links: 10SP, 100SP, 500SP, 1000SP or Another amount