A hitchhiker guide to the quest for dark matter
In my particle physics work, I spend a decent fraction of my time in studying the phenomenology associated with theories beyond the Standard Model of particle physics.
How to construct such a new physics theory? The idea is pretty simple. One starts from the Standard Model and extends it, for instance, by enlarging the symmetries behind it or its particle content. This generally allows one for curing some of the flaws of the Standard Model. Which flaws? Well, as an example among several others, the Standard Model does not provide any successful explanation for the dark matter pervading our universe.
For this reason, most of the currently studied options for new physics contain a new particle that is a candidate for dark matter. An excellent class of candidates is comprised of the so-called weakly-interacting massive particles or WIMPs (this is the acronym of the previous words), and such candidates are very common in many theories beyond the Standard Model.
Of course, all of this is relevant under the condition that we accept the hypothesis that a large fraction of the matter in the Universe consists of a form of matter that is dark (i.e., it does not interact electromagnetically). There are alternatives theories, like MOND theories (see here for some information on such theories or check the publications of Mordehai Milgrom) but I will not discuss them.
There is a wealth of advantages to postulate the existence of dark matter, since this gives straight explanations for the rotation curves of the galaxies, the cosmic microwave background data, big bang nucleosynthesis, etc.
 [image credit: NASA ]
[image credit: NASA ]
In the case where one would like to study a theory of new physics that contains a dark matter particle, a good question to ask would be how to search for such a particle?
There are several ways that are all summarized in the picture below that I will explain all along this post. I there denote the dark matter particle by DM and any Standard Model particle by SM.
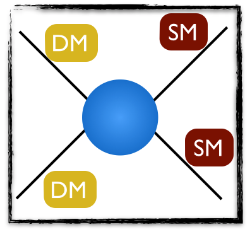 [image credits: mine]
[image credits: mine]
THE RELIC DENSITY OF DARK MATTER
In the early universe, dark matter is in thermal equilibrium with the surrounding cosmic soup of particles (see here for more information). The rate at which dark matter particles annihilate equal thus the one at which they are created.
The Universe is however cooling down with time, so that at some point, it becomes too cold for dark matter creation to occur. Consequently, dark matter particles continue to annihilate with each other, until very few guys are left. The Universe going on with it expansion, the remaining dark matter particles soon start to be very diluted in it, and there is very little chance that at this stage, a given dark matter particle can find a companion to annihilate with.
For these reasons, we talk about a thermal relic of dark matter, and we say that the dark matter density has frozen out.
We are thus left with a specific amount of dark matter particles today, which has been be measured by cosmology experiments. From the particle physicist standpoint, this implies that we have some data to compare our predictions with.
In other words, we can take our favorite model of new physics, evaluate the relic density of dark matter and compare it with data.
And now we can come back to the image I sketched above.
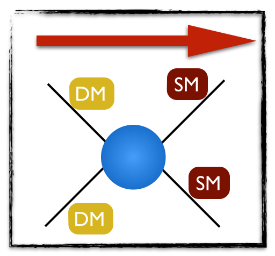 [image credits: still mine… ]
[image credits: still mine… ]
If we read the above diagram from left to right, it represents two dark matter particles annihilating (via some interactions hidden in the blue blob) into a pair of Standard Model particles.
Using the Feynman rules relevant for the physics model under consideration, we can calculate the annihilation rate of these two dark matter particles into any pair of Standard Model particles (see here for more information on Feynman diagrams). Summing then upon all possible final states, we end up with a prediction for the total dark matter annihilation rate. This annihilation rate is the input needed for computing the relic density of dark matter.
The relic density of dark matter hence provides a first handle to test new physics models featuring a dark matter candidate: this candidate must have the correct relic abundance and hence satisfies the observation.
DARK MATTER DIRECT DETECTION
Physicists are trying for several decades to directly observe dark matter when it travels through Earth.
The idea is to build a huge detector and try to measure very rare nuclear recoils that are induced by the collision of a dark matter particle and a nucleus being part of the detector material.
Since dark matter is very weakly interacting, such events are very rare and thus difficult to observe from the background. Such an even could indeed be easily mimicked, for instance, by a neutrino hitting a nucleus, which is also rare but not as rare.
After decades of improvement, the two best experiments so far are the LUX experiment (a 370 kg detector made of liquid Xenon) and the CMDSLite experiment (a 10 kg detector made of Germanium).
 [image credits: LUX ]
[image credits: LUX ]
As everybody probably knows it, dark matter direct detection experiments have so far not been able to observe any dark matter particles, so that they have instead been able to put an upper limit on the rate at which the dark matter particles should interact with different atomic nuclei.
As for the relic density, we have thus data with which we can compare the theoretical predictions.
Those predictions are obtained from the figure below, which is the same as before except that we read it from top to bottom
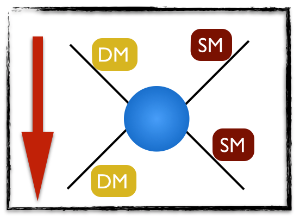 [image credits: mine again]
[image credits: mine again]
A Standard Model particle SM and a dark matter particle DM scatter elastically (via some interactions hidden in the blue blob). The initial-state particles and the final-state particles are the same, which is why to discuss elastic scattering.
A small technical difficulty in the calculation is that the Standard Model particle (that is actually a quark or a gluon) must be linked to the atomic nucleus it is a constituent of to map the experimental setup. But this again can be calculated, everything is alright :)
Dark matter direct detection experiments put strong limits on the rate at which dark matter would interact with different species of atomic nuclei. As a result, we have a second handle for constraining new physics theories containing a dark matter candidate.
COSMIC RAYS
 [image credits: Wikimedia ]
[image credits: Wikimedia ]
Some regions of the Universe are expected to exhibit a high density of dark matter. Two examples consist of the center of the Milky Way and dwarf spheroidal galaxies that are very low-luminosity small galaxies containing a reduced amount of stars and a lot of dark matter (relatively), as described for instance in this post.
Consequently, it is likely that dark matter particles can annihilate with each other in these regions of the Universe. The annihilation products can then be observable with dedicated experiments under the form of cosmic rays . For instance, the annihilation of a pair of dark matter particles into a pair of photons could give a gamma ray signal observable within the Fermi Large Area Telescope.
As for the two cases already described, we have thus data, so that we can compute the associated theoretical prediction and test our model of physics beyond the Standard Model.
In this case, we need to read our usual sketch from left to right again: two dark matter particles annihilate into Standard Model particles (that are taken to be photons for gamma rays predictions).
 [image credits: you know now]
[image credits: you know now]
Cosmic rays, and gamma rays in particular, give thus a third handle to constrain physics models with a dark matter candidate, as we ca calculate the new physics contributions to the cosmic ray spectrum that would be observed on Earth.
COLLIDER SEARCHES
 [image credits: CERN]
[image credits: CERN]
Finally, dark matter can also be produced at colliders such as the Large Hadron Collider (the LHC) at CERN, and thus potentially observed. Having a plethora of LHC data, we can compute new physics predictions and extra constraints on the viable models.
Predictions once again rely on the same diagram shown before, but we need to read from right to left this time
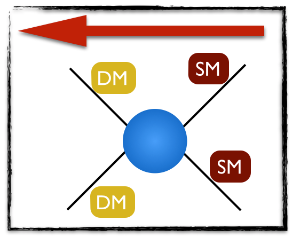
Two Standard Model particles (the constituents of the colliding protons) annihilate to give rise to a pair of dark matter particles.
There is however a little complication related to how an LHC detector works. In the above process, we produce two dark matter particles from a proton-proton collision that are weakly interacting. There is consequently not a single chance those dark particles will leave any track in the detector.
In short, one produces nothing visible and as a result, the detectors do not trig and nothing is recorded. All collisions yielding the production of a pair of dark matter particles are lost.
But the story does not end here. There are actually many ways out. The key idea is to consider dark matter production in association with something visible. Equivalently, we produce a pair of dark matter particles and a third visible particle.
The visible object must be highly energetic so that the detectors will trig and record the associated events. From the properties of the visible one can then reconstruct the properties of the invisible by making use of momentum and energy conservation. These two conservation laws (that consist of a unique law in special relativity) allows us to deduce what is missing/invisible from what is visible.
There are many of such analyses, the most common ones relying on monojet, monophoton and monoHiggs probes. The monoX name only means that a single X particle is produced in association with a large amount of missing energy (connected to the pair of dark matter particles). And we can replace X by any Standard Model particle.
Particle colliders hence provide us a last means, and more precisely several ways, to constrain dark matter particle properties from the production of a pair of dark matter particles together with a visible particle that can be studied.
COMPLEMENTARITY IN ACTION - AN EXAMPLE
As an example, I will discuss one of my latest scientific article where together with my collaborators, we have studied simplified models of dark matter from all the above-mentioned aspects. This is what is called a comprehensive approach using the complementarity of different probes for dark matter.
The simplified model of new physics under consideration is constructed as follows: we take the Standard Model, we add a dark matter candidate that we name X and a mediator that we name Y. The Y particle is called a mediator as it connects the dark matter particle to the Standard Model. We have explicitly imposed that the mediator only interacts with the dark matter particle and the top quark for the sake of the example.
After applying all the constraints described, we end up with the figure below where we represent the new physics configuration that are allowed by data. The axes consist of the mediator and the dark matter particle masses.
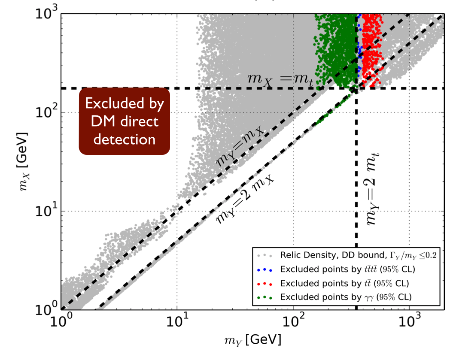 [image credits: arXiv]
[image credits: arXiv]
- The grey points are the points satisfying all constraints.
- The colored points are the points satisfying all cosmology constraints but excluded by the LHC.
- The left-upper corner is excluded by dark matter direct detection results.
- In the other white region, the relic density of dark matter is not correct reproduced.
Thanks to the usage of many data from many different (complementary) sources, our new physics model is actually strongly constrained. New data will in the future allow us to constrain it more and more (or discover it if we are lucky).
SUMMARY - TAKE HOME MESSAGE
There are many ways to search for dark matter. Not only in the sky, but also on Earth.
Suitable experiments include:
- cosmology experiments aiming to measure the dark matter relic density, observe its passage through Earth or , its influence in the cosmic ray fluxes;
- collider experiments where dark matter can be directly produced.
So much mystery still surrounding the nature of the universe.
Great post @lemouth, dark matter is very mysterious to me. I am grateful for these posts like this as they allow me to get a bit of a better grasp over these particles and what they are.
Edit: Forgot to say, I really like the title. :)