
VIDEO INCLUDED!
In this short article I will explain the very basics about how rockets reach orbital trajectories. I have linked an "educational" video to better show what happens during the orbital insertion.
Introduction
In order to get a stable orbit around the Earth it is not enough to reach a high altitude: in fact, in this case the object or the rocket will soon hit again the ground. To achieve an orbital trajectory it is also necessary to have a horizontal speed or an orbital speed (the speed at which the object orbits around the center of gravity of the Earth). The higher is the altitude, the lower is the orbital speed. For instance, this is well deductible by the motion of the planets around the sun: the orbital speed of Mercury, the closest planet to the sun, is equal to 47,36 km/s (average) whereas Neptune, the farther planet, has an orbital speed of 5,432 km/s (average). I had to point out that the orbital velocities are average since the orbital trajectories of the planets are not perfectly rounded but rather elliptical. This means that when they are in proximity of the perihelion (the closest point to the sun) they have a higher orbital speed if compared to the one at aphelion (the farther point from the sun).
How object can stay in orbit
To understand the orbital speed we can start a mental experiment, designed by Newton1, as shown in the picture (fig. 1).
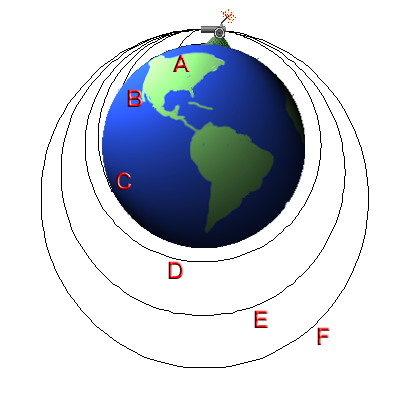
Fig. 1. Source Wikipedia.
We can imagine to shoot a cannon ball from the top of a very high mountain. After a short time the cannon ball will fall at a given distance (A) which is determined by the starting height and the force. Firing once again the cannon ball by applying a greater force, the cannon ball will land at a greater distance (B). Let's fire the cannon ball (C) with a still greater force, the cannon ball will fall farther than the previous case. Now (refer to the picture) we have to consider that the curvature of the Earth influences the falling distances. In the latter case (C) and in part in case (B), we have to consider that while the cannon ball is falling to the ground the surface curves and gradually lowers. Thus, while the cannon ball approaches the ground, the ground itself gets away due to the curvature. Since the cannon ball approaches the ground at a higher speed than the ground lowers, soon or later the cannon ball will fall. Considering this mechanism we can therefore imagine shooting the cannon ball with a specific force so that the falling speed and the lowering speed of the ground are equivalent: done, the ball is in orbit! Of course, this model is an ideal model where other forces, such as the air frictions do not act. For what we said, the cannon ball is in constant fall approaching the ground that meanwhile gets away. For instance, the microgravity experienced by the astronauts working in the International Space Station (ISS) is not due to the reduced gravity but is indeed the result of the constant-fall mechanism! In fact, the ISS orbits around the Earth at 400 km and is subjected to the 80% of the gravity force. Moreover, given the friction due to the presence of air molecules even at a height of 400 km, a periodic correction of the trajectory is necessary.
So, how rockets get to orbit? First step: choose a launching site
Most of launching sites are as close as possible (considering the nation borders) to the equator. In fact, as we saw, to get into orbit it is necessary a horizontal velocity. We have to take into account that the Earth is a rotating system around its axis. Thus, as a slingshot, launching a rocket from the equator toward east will have a certain amount of momentum2. More, the resulting orbit of a rocket launched from the equator will be on Earth’s rotation plan, that is almost shared with other planets which will make it easier to reach them2. Conversely, launching a rocket from a further north site, the resulting orbital plan would be inclined and it would be necessary to consume propellant to reach the equatorial plan (fig 2).
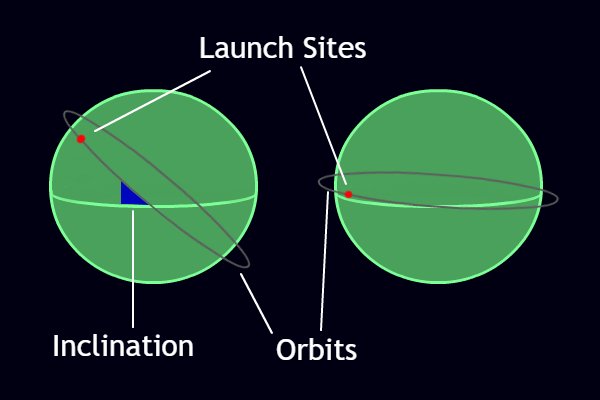
figure 2. Schematic drawing. Source me.
Second step: launch the rocket
The rockets are launched vertically because they have to pass as soon as possible the first 10km (36000 ft): the most dense part of the atmosphere, thus the one offering the major friction. After 10km the rocket starts what is called gravity turn: it gradually tilts pandering the gravity and dynamic forces, limiting the transversal forces until the rocket is parallel to the surface3. Once reached this point the thrust of the rocket's engines will be used exclusively to increase the orbital speed and to circularize the orbital trajectory (you can see this in the final part of the video).

fig. 3. A rocket heading to east during sunrise. Screenshot realized withKerbal Space Program. Source me
Delta-V: the energy cost to reach your destination
The delta-V is the difference between the final velocity and starting velocity and it represents the energy cost to reach a rocket's destination4. The Delta-V necessary to reach the Low Earth Orbit (LEO) is 9.3 Km/s. LEO is an orbit between 160 km and 2000 km (100 miles and 1240 miles)5. The lower limit is imposed by the atmosphere: below that limit the friction will drastically decrease the lifespan of a satellite. The upper limit is imposed by the radiations originating from solar wind and corresponds to Van Allen radiation belt. Above this limit, radiations would cause anomalies to satellite instruments and their failure. The picture below (fig. 4) shows the delta-V’s necessary to reach a point from another. To calculate the delta-V just sum the various delta-V’s met going from the starting point to the final point.
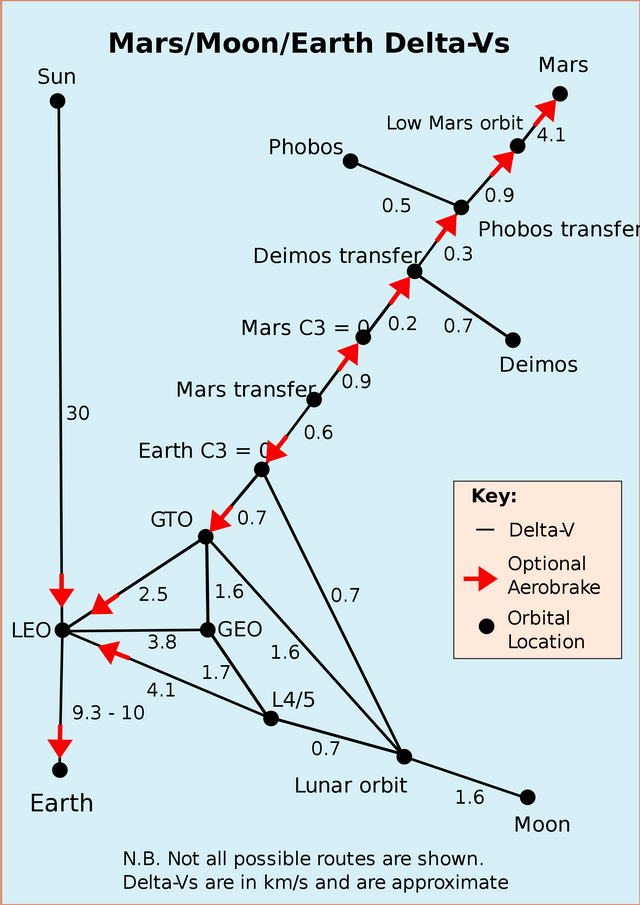
Fig. 4. Source Wikipedia. This picture shows the delta-V map necessary to reach a destination from a specific starting point
The video
Here a short video that makes easier to understand what is explained in this short article and the various phases of a rocket’s launch. In the first part of the video the vertical launch of the rocket enables it to pass the first 10 km, then it starts the gravity turn phase and finally the suborbital trajectory is circularized to reach an orbital trajectory. The video editing is quite amateurish and may contain inaccuracies. For instance, a real rocket reaches the orbital speed at the apogee and then finishes the engine burn, instead the video shows the rocket taking a pause until it reaches the apogee to start then again the engines in order to circularize the orbit. More, it is not possible to turn off and on a rocket's engine so easily while flying. The video has been realized with
Kerbal Space Program (KSP) and various mods among which
KOS which allows to write and use scripts (kerboscript is the name of the language) executable by the rocket.





interesting. but is the earth spining or sun moving around us? always get confused. they said it was flat then i fell off the ball?
Actually the Earth is a donut :-)
Nice post! Especially with the images from Kerbal Space Program. I absolutely love that game.
Thx! Finally it answered a human
I thought the post was readable only from bot :-D
Hah! That's what it looks like. Maybe also the topic is more for rocket scientists... Or people who play KSP ;D
Congratulations @ginlucks! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @steemitboard:
SteemitBoard and the Veterans on Steemit - The First Community Badge.
An educational overview on the space rocket launch problematic! The Kerbal Space Program seems like a cool thing for my astronomy class, do you think it could be useful to elementary school kids? Is it too complicated?
It depends how much are you able to use it. You may show only the problems that you want to show :D. Honestly I do not know how much elementary school kids would be able to use this game because it is complicated, for instance you have to consider how t build a rocket (however there are some stock available models) antenna connections, signal delay, charge of batteries, drag and dynamics (pic)
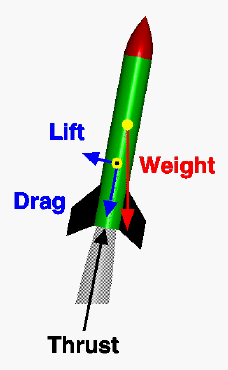
and so on but surely it is a nice tool to make them curious about astronomy. Especially if they see you play it just because you know certain things that they don't... probably they would know these things too. There are a lot of video tutorials on web, check them. However you may also use cheats to make it easier. I can suggest you also two other software for your astronomy class: Universe Sandbox (29$) and Space engine (free)
Congratulations! This excellent post was chosen by the new curation initiative of the @postpromoter content promotion service to receive a free upvote!
This post exemplifies the type of great content that we at @postpromoter enjoy reading and would love to see more of on the Steem platform. Keep up the good work!
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
I am honored :-)
You have recieved a free upvote from minnowpond, Send 0.1 -> 10 SBD with your post url as the memo to recieve an upvote from up to 100 accounts!
Congratulations @ginlucks! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPYou got a 13.97% upvote from @postpromoter courtesy of @postcurator!
Want to promote your posts too? Check out the Steem Bot Tracker website for more info. If you would like to support the development of @postpromoter and the bot tracker please vote for @yabapmatt for witness!
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by ginlucks from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.