Curious Mathematics: Hedgehogs, why cyclones exist and why 3-dimensional humans can't have nice hair
Hey guys,
do some of you happen to have short to medium long hair? If so, I am inclined to presume that at least some of you have been pondering about the following issue:
If you find yourself in agreement with this, worry not! As it turns out there is no one to blame for this except for mathematics - at least in a theoretically idealized setting abstracting from reality. Let's discuss one of those rare mathematical statements with immediate applications to reality, at least if you take everything I'm going to say with a grain of salt :)
Hedgehog Theorem
To understand why this very peculiar phenomenology emerges from mathematics we take a look at one quite funny theorem from the discipline of algebraic topology, the so-called Hedgehog theorem also known as Hairy ball theorem.
Appearing to be pun at first glance, this rather peculiar (but legitimate) terminology is in fact a direct reflection of the theorems "practical" implication. Colloquially speaking it states that you can't comb a hedgehog flat or -more generally speaking- a hairy ball such as a coconut.
To make matters more precise, the hedgehog theorem deals with a question of existence of certain vector fields on the n-dimensional Sphere Sn which you can think of as the surface of a ball in the ambient (n+1)-dimensional space Rn+1. In particular it states that:
or in other words
(A short idea of proof can be found at the bottom of this article)
Wait, what does this have to do with hedgehogs? Well, mathematically speaking (albeit with slight imprecision), the surfaces of hairy balls such as hedgehogs and coconuts correspond to 2-dimensional spheres in our 3 dimensional space while orderly combed hair or spikes would coincide with a nonvanishing continuous tangential vector field.
But since 2 is even, the hairy ball theorem asserts the non-existence of such an object, i.e. we can not comb the hedgehog properly. Any attempt to do so is mathematically and irrefutably bound to fail in at least one regard, in the sense that no vector field on S2 (embedded in R3) can be continuous, nonvanishing and tangential at the same time.
If we assume continuity as a property, we observe that any hypothetical combing of the hairy ball fails in one of the two ways: The vector field vanishes in some points (a bald spot) or fails to be tangential everywhere (a tuft, see Fig. 1 below)
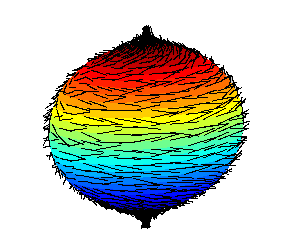
Bad hair
Going back to physical reality, we have to acknowledge that the average human scalp is not equivalent (e.g. homeomorphic, diffeomorphic, homotopy equivalent etc.) to the sphere S2 in terms of algebraic topology which stricly speaking renders the hedgehog theorem not applicable. (Comparing it to a half-sphere would be more accurate, but the theorem is not applicable for those either)
Interestingly enough and by empirical evidence, human hair still exhibits some of the phenomena which cause the ideal combing of the hairy ball to fail:
Either your hair refuses to align with your skull pointing in crazy directions or forms a cyclonic pattern (a whirl) around a tiny bald singularity on your head.
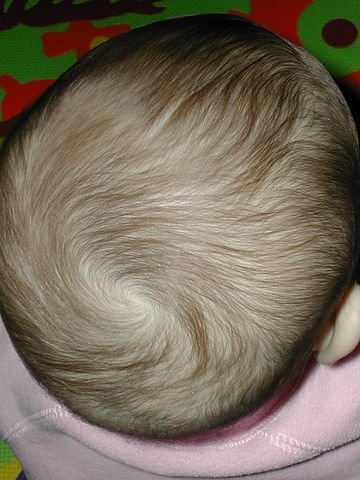
Why reality conforms to the idiosyncrasies of algebraic topology even though there is no immediate mathematical necessity to do so eludes my knowledge. Of course reality can be arbitrarily complicated and feature physical annd biological effects that we have not accounted for. But hey, it's always fun to conspire, maybe fate takes revenge on us giving us perpetually wild and reluctant hair.
Cyclones
Another very interesting and a little bit more rigorous implication to derive from mathematics of hairy balls (pun intended) can be found in meteorology. Roughly speaking, the hedgehog theorem asserts that at any given time there has to be at least one perfectly windless spot and one active (but maybe small) cyclone (hurricane, typhoon) around it somewhere on Earth.
Why is that? In a sufficiently good approximation on a large scale we can consider the Earth's surface as a perfect sphere with a purely tangential/horizontal flow of air (wind) with continuous wind speeds. Those wind speeds can be represented as a vector field just as we identified hair length/orientation with a vector field. By our above theorem we no that said vector field can't be nonvanishing, i.e. there hast to be some perfectly calm spot in which the local wind speed vanishes.
This mathematical model does not strictly guarantee cyclonic patterns of wind flow yet, but physical arguments typically suggest their formation: We expect air to be a conserved quantity and therefore wind to fulfil some continuity equation. Furthermore wind on the rotating Earth is subject to the Coriolis force which forces the air into a rotation about the windless "eye of the storm".
To conclude:
Even though all of this has to be taken with a grain of salt since reality does not perfectly conform to reality and vice versa it is instructive to observe how many real world implication an inconspicuous theorem of pure mathematics can have ;)
Thanks for reading and have a nice day!
Sources and references
- I. Agricola, T. Friedrich; Global Analysis: Differential Forms in Analysis, Geometry and Physics
- https://en.wikipedia.org/wiki/Hairy_ball_theorem
- Fig. 1: The Evil Midnight Uploader what Uploads at Midnight at English Wikipedia - Transferred from en.wikipedia to Commons., Public Domain, Link
- Fig. 2: NoJhan (talk) - originally posted to Flickr as DSCN2483, CC BY-SA 2.0 fr, Link
P.S. (Idea of Proof)
Assume the desired vector field v(x) existed. Define H: Sn × [0,1] → Sn by mapping (x,t) to the the point x geodesically transported by angle tπ along a great circle in direction v(x). H defines a homotopy between the identity and the antipodal map on Sn. But for even n, the identity is orientation preserving while the antipodal map is orientation reversing which is a contradiction.


Being A SteemStem Member
The simplest way to introduce the hairy ball theorem is to study the Euler formula for graphs on the sphere. The graphs on the sphere then naturally define a vector field. For a video about this see over here
Note that in some sense this is exactly how the proof works in terms of homology since the problem is reduced to a problem for simplicial complexes.
As a fun addendum check this page
PS maybe you should put a source for all the photos?
Well you could argue that it is just a corollary of the Poincaré-Hopf theorem, but I would not consider that the easiest proof. Correspondingly there are several approaches but you don't absolutely have to introduce simplicial complexes. ^^
Lengthy image sources are in the list at the bottom 👍
Nice links, by the way. I did not know "Uncyclopedia" before, although there is a conceptually similar page called "Stupidedia" in Germany :D
I think you misunderstand me. The note part in my reply is a note. My claim is that the simplest way to explain it is using the Euler formula and then show that graphs generate vector fields. All of this can be explained visually.
You don't need Poincare-Hopf, simplices etc. but they connect nicely to the previous method.
Wao That's so nice
It's great.
Great information @galotta.
Loved and impressed by the way you explained and shared with us,keep your good works up.have a great time and hope you will get a bright future.