Sets of Julia part II

Hello to all, today I bring the second part on my study of sets of julia, in the previous post (https://steemit.com/science/@falcao12/sets-of-julia) only cover the part of the set of real numbers in this post will see what happens in the conjunct of complex numbers:

R = (−∞; −1,5) ∪ [−1,5; 1,5] ∪ (1,5;∞)

In figure 1 the green line represents the Julia set of the function:

F (x) = x^2 - 0.75

Let us now study the same function but in the complex plane, that is,

F (z) = z^2-0.75

Where z is a complex number, that is, z = a + ib with a, b ∈ R and i =√-1

What happens when the value a0 is a complex number instead of a real number?

Let a0 = i have the following

a0 = i
a1 = f (i) = i^2 - 0.75 = -1.75

Note that a1 is a real number less than -1.5 therefore by analysis of previous post (https://steemit.com/science/@falcao12/sets-of-julia) {ak: k ∈ N} escapes to infinity .

If a0 = 0.5i then

a0 = 0.5i
a1 = f (0.5i) = (0.5i)^2 - 0.75 = -1

For this case a1 is a real number belonging to the closed interval [-1.5; 1,5], in consequence {ak: k ∈ N} converges.

In general if we take a0 = ci where c ∈ R then the condition that must satisfy c that {ak: k ∈ N} converges is as follows:

-1.5 ≤ (ci)^2 - 0.75 ≤ 1.5
−0,75 ≤ −c^2 ≤ 2,25
0 ≤ c^2 ≤ 0,75
−0,866 ≤ c ≤ 0,866

That is ci must be between -0.866i and 0.866i

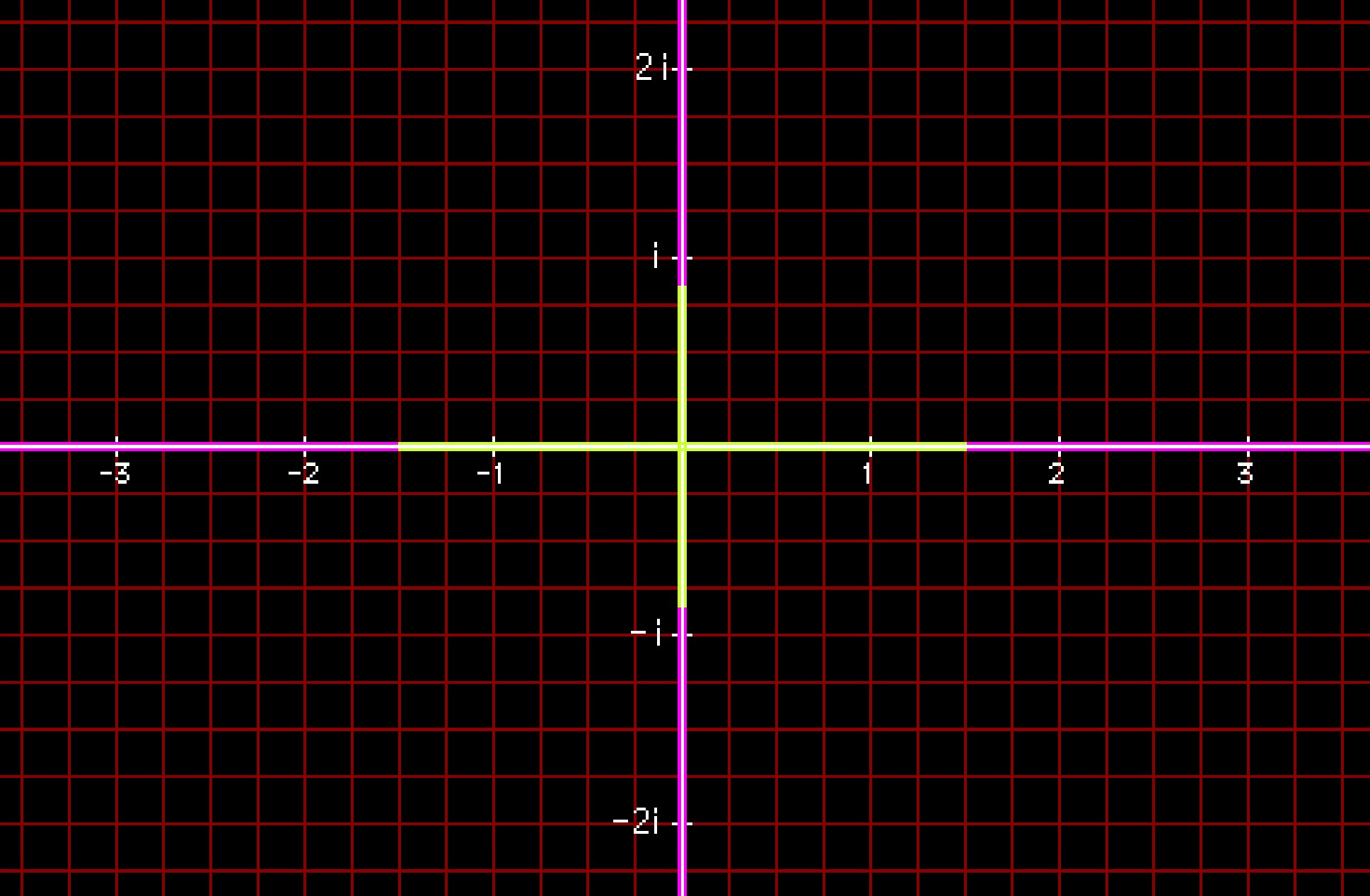
In figure (2), the green part represents the julia sets of f (z) = z^2 -0.75, but only referring to the real axis and imaginary axis, that is to say we still have to study initial points of the form a0 = a + ib where a, b ∈ R - {0}

study of the initial points of the form a0 = a + ib where a, b ∈ R - {0}

If we take a0 =1/3 +5/9i we get the following iterations
a0 =1/3 +5/9i
a1 = f (1/3 +5/9i) = (1/3 +5/9i)^2 - 0.75 = -0.9475 + 0.3704i
a2 = f (-0.9475 + 0.3704i) = (-0.9475 + 0.3704i)^2 - 0.75 = 0.0106 + 0.3704i
a3 = f (0.0106 + 0.3704i) = (0.0106 + 0.3704i)^2 - 0.75 = -1.2424 + 0.0149i
a4 = f (-1.22424 + 0.0149i) = (-1.22424 + 0.0149i)^2 - 0.75 = 0.7933 - 0.0371i
a5 = f (0.7933 - 0.0371i) = (0.7933 - 0.0371i)^2 - 0.75 = -0.1221 + 0.5891i

In this case it is not clear what will happen as the number of iterations progresses, therefore it is time to carry out the calculations with a computer and a software, which in our case is MatLab

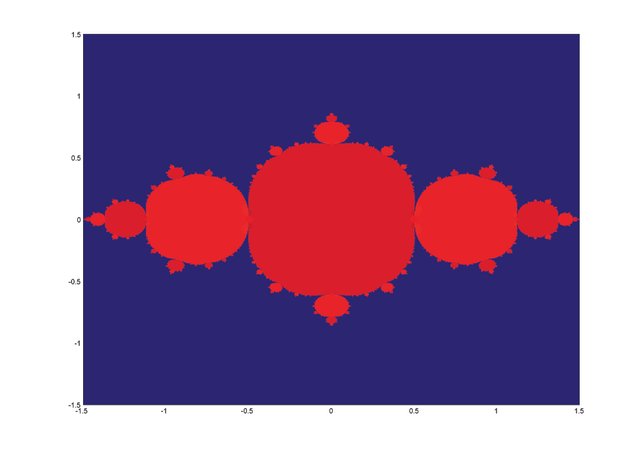
The figure (3), made in MatLab, we show the julia set of f (z) =z^2 - 0.75, where each starting point a0 = a + bi is taken in such a way that (a, b) ∈[-1.5; 1.5] × [-1.5; 1,5] and 400 iterations were done to study in behavior of {ak: k ∈ N}, the blue color indicates that the succession escapes to infinity, the Julia set in a reddish color is painted.

enjoy, resteem and follow me @falcao12