a modification of the Newton method
Hello to all my friends from the steemit community, especially to the scientific community, on this occasion you present three images that represent the basins of attractions of a modification of the Newton method developed by me. The method shows an excellent behavior as can be appreciated in the images.
To understand a little better the images, let's see the following: Suppose we have any numerical method to solve nonlinear equations, ie f (x) = 0, where f is a non-linear equation,
Exp (x / 2) * cos (2x) = 4;
This problem which represents the oscillation of a structure, equipped with a damping system, before an oscillatory movement, is impossible to solve by simple analytical means.
For this, there is a wide range of algorithms that solve this type of problem, among them the Newton method whose order of convergence is 2, the Chebyshev method and the Halley method of order 3 each and we can even find a Family of methods of order 3 such as the Chebyshev-Halley Family
Because there are many numerical methods is necessary to try to see, somehow, that method is better than another, there are measures that allow sorting methods, such as: order of convergence, efficiency measures, number of functional assessments in each iteration , etc.
In the last decades has emerged a useful and powerful tool that allow us to make qualitative comparisons between methods, this tool in known as the basin of attraction.
The basin of attraction allows to see the behavior of the method according to different initial points, in other words, an initial point quantity is taken in the complex plane with which the method is started, if given one of those initial points the method converges Then it is painted of a certain color taking into account towards which root occurred the convergence but not happens convergence is painted of black color. The result of this is what we appreciate in the following images:
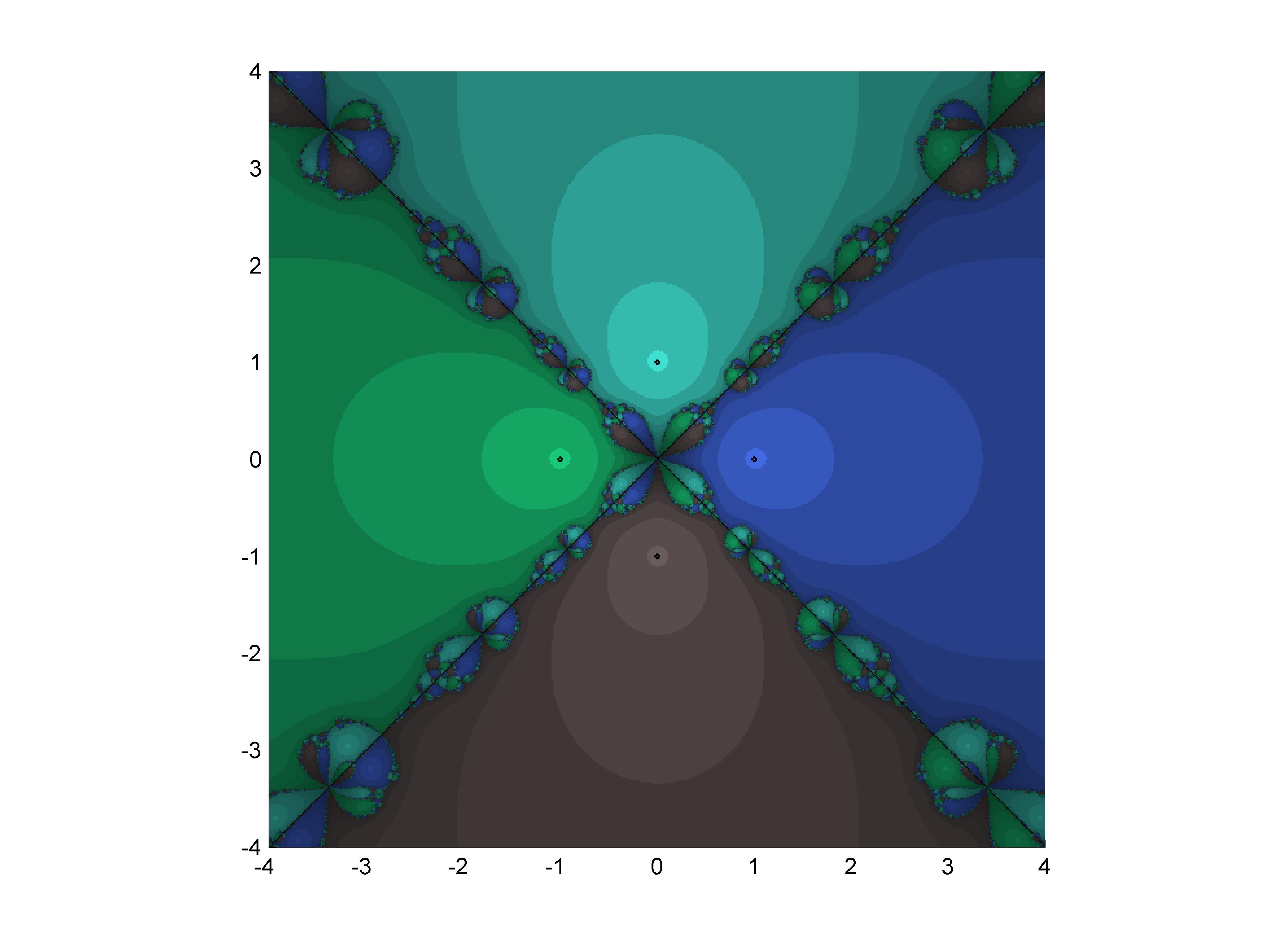
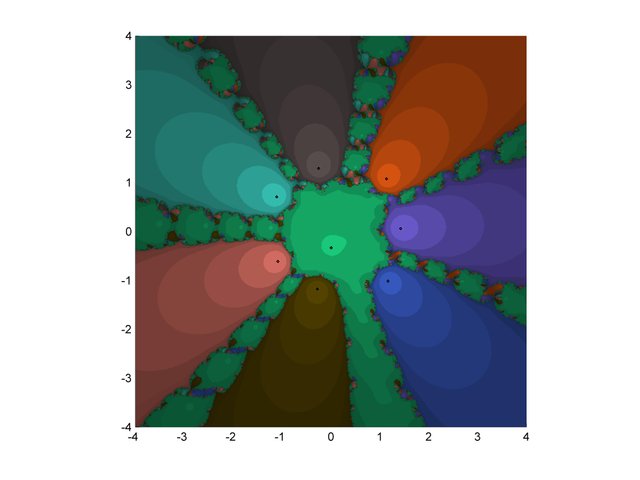
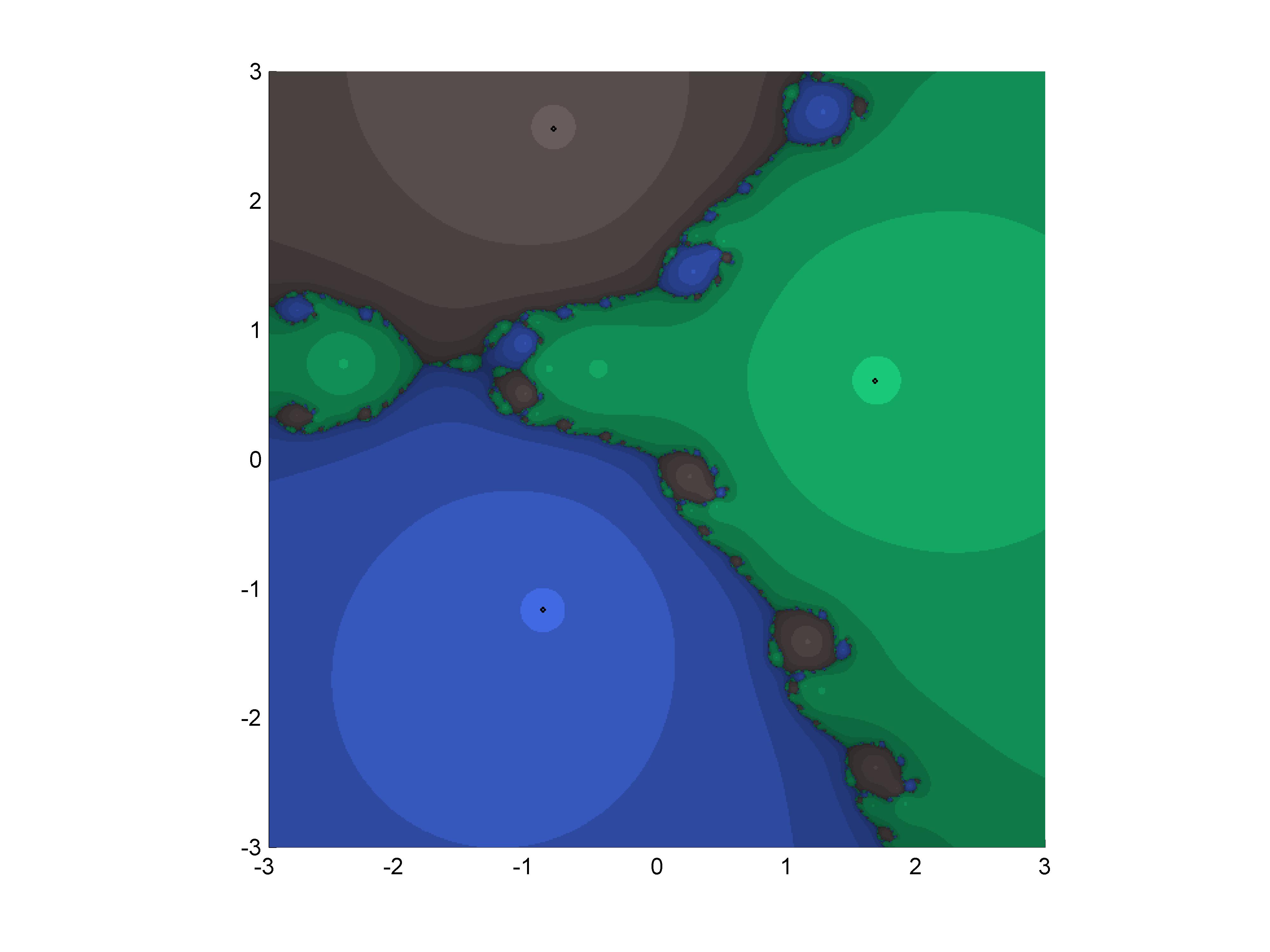
enjoy and follow me @falcao12
looks amazing but it's over my head (-: cool looking graphs
Congratulations @falcao12! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP