diffraction patterns
we can look inside crystals using x-rays and neutrons.
in the simplest case of elastic scattering, the incoming and outgoing wavevectors have the same magnitude, that is |k| = 2 π /λ . here, there is no energy transfer, only a change of direction of the photon or neutron, which is later detected on an area detector and is stored as a count in a histogram at a particular energy (time of flight).
elastic scattering is described by the Laue equations, which state the conditions for constructure interference that lead to scattering. the well known Bragg equation neatly summarises this: 2d sinθ = nλ , where n is an integer which describes the order of reflection and d is the spacing between lattice planes.
by measuring the sample at lots of different orientations, we can build up a 3-dimensional representation of the crystal structure.
x-rays interact with the electron cloud that surrounds each atom in the crystal sample.
neutrons are particularly useful since they are actually fermionic with spin s=1/2. this allow us to study magnetic properties by looking at the correlations of spins. if the sample has a periodic magnetic structure, we can detect magnetic Bragg peaks akin to that observed in x-ray experiments.
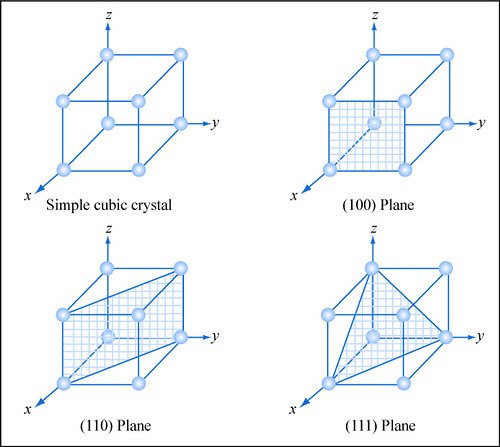
here are some simulated diffraction patterns from the principal lattice planes (100), (110) and (111) of the simple cubic structure. notice the threefold symmetry in the (111), four fold symmetry in the (100) and two mirror planes in the (110).