Deflexiones en Vigas elásticas Isostaticas

Hola amigos y queridos estudiantes les dejo un artículo sobre los principales métodos para el cálculo de las deflexiones en vigas, luego subiré otros con ejemplos resueltos y propuestos.

Métodos de Cálculo de las Deflexiones en Vigas

Introducción

Los elementos que forman una estructura están hechos de materiales que se deforman al cargarlos. Si sus deflexiones exceden de valores permisibles, ello puede repercutir en la apariencia estética de las estructuras y los materiales fijados a esos elementos pueden resultar dañados. Por ejemplo, un nervio o correa que se deforme en exceso puede causar grietas en el yeso utilizado comúnmente como cielo falso o inclusive en el concreto y materiales usados como acabados como mármol o cerámica. Por otra parte, una estructura no debe vibrar o deflactar demasiado para que parezca “segura” a sus ocupantes. También el cálculo de las deflexiones es esencial en el cálculo de estructuras hiperestáticas.

La práctica normal en Venezuela y en muchos países del mundo, es limitar las deflexiones causadas por las cargas actuantes (generalmente la variable o viva) a un valor inferior a L/360 donde L es la longitud o claro del tramo de viga analizado. Sin embargo estas restricciones pueden cambiar en función del uso y del tipo de la estructura.

A lo largo de los años se han formulado varios métodos para el cálculo de las deflexiones, las cuales en forma generales se deben los efectos de fuerza axial corte y momento. En el caso particular de las vigas no existen efectos de fuerza axial y para las relaciones de peralte o relación H/L (Altura/longitud generalmente > 10) el efecto de las deformaciones por corte puede despreciarse, por lo tanto la mayoría de los métodos y procedimientos formulados para calcular sus deflexiones se basan solo en las deformaciones por flexión.

En este orden de ideas, en este artículo determinaremos las deflexiones elásticas de vigas utilizando los métodos de doble integración o formulado por Henry Navier, métodos geométricos como los formulados por Charles Greene y Otto Mohr y métodos Energéticos como los basados en trabajo virtual (originado a partir de los enunciados de Daniel Bernoulli) y en el teorema de Castigliano. Cada uno de estos métodos, tienen ventajas y desventajas que serán expuestos cuando sean presentados.

Teoría de la Viga Elástica

De los trabajos de Euler, Bernoulli y Coulomb, se obtiene que una viga prismática sometida a flexión pura se flexiona en forma de arco y que, dentro del rango elástico, la curvatura de la superficie neutra puede expresarse a partir de la relación 1/ρ = M/EI. Donde 1/ρ representa la curvatura o el ángulo de las paredes aun planas de un diferencial después de la flexión, M el momento flexionante interno y EI el módulo de rigidez a flexión que proviene de la multiplicación del módulo de Young (E) y de la Inercia de la sección (I).

También de las ecuaciones del cálculo matemático, la expresión matemática que gobierna la curvatura de un arco viene dada por:

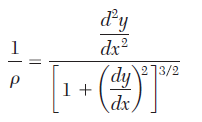(1)

Donde en el caso de las deflexiones la variable y representa la deflexión, flecha o el bajamiento. Por lo tanto, se tiene que:

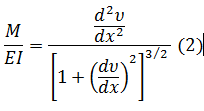
La cual representa una ecuación de segundo orden no lineal. Su solución, ν = f(x, d la forma exacta de la curva elástica solo por efectos de flexión. Esta ecuación puede aproximarse de forma importante al considerar que dv/dx son valores pequeños y su cuadrado aún más pequeño y por lo tanto la expresión del denominador tiende a 1 en casi todos los casos y por lo tanto la expresión anterior puede tomarse como:

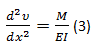
Por otra de esta hipótesis también resulta que el ángulo que describe la intersección de los planos rotados durante la flexión (dθ), es igual a la longitud del arco (ds) entre el radio de giro (ρ), es decir:

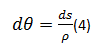
Al asumir que dv/dx era prácticamente cero también se asume que ds = dx y por lo tanto la expresión anterior resulta:

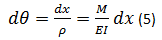
ó

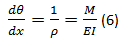
Método de la doble integración

Navier fue el primero en darse cuenta que la ecuación 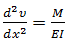es una ecuación diferencial ordinaria, lineal, de segundo orden. La cual para una prismática (aquellas de sección constante) puede multiplicarse ambos miembros de la ecuación por EI e integrar en x una y otra vez, se puede escribir,

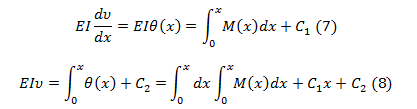
Las constantes C1 y C2, se pueden determinar mediante las condiciones de borde o frontera, dicho con mayor precisión, de las condiciones impuestas en las vigas por sus apoyos, por ejemplo los valores C1 y C2 representan los valores de la rotación y deflexiones al inicio de la viga.

Si en una viga existen varias condiciones de cargas entonces para cada tramo salen dos constantes de integración y para su solución se requerirá además de las condiciones de borde, condiciones de continuidad tanto a nivel de rotaciones como de las deflexiones. También en estos casos, se puede ir dejando los valores de rotación y deflexión en los extremos de cada tramo en función de C1 y C2 y determinar sus valores con las condiciones de borde.

Por lo tanto los pasos que se deben seguir para este procedimiento son los siguientes:
a. Se determina la(s) ecuación(es) de Momento Flector
b. Se establecen las condiciones Iniciales, de borde y continuidad en el caso de que sean necesarias.
c. La(s) ecuación(es) se integra(n) una y otra vez para obtener la familia de soluciones de la deflexión
d. La solución particular se obtiene al establecer un sistema de ecuaciones con las condiciones de borde y continuidad o al dejar los valores extremos de cada tramo en función de las primeras contantes C1 y C2, haciendo uso de las condiciones de continuidad y determinándolas con las condiciones de borde.

La principal ventaja del método de doble integración es que se puede obtener una expresión matemática para calcular las deflexiones y rotaciones a lo largo de toda la viga. La principal desventaja radica en la cantidad de operaciones necesarias para resolver el sistema de ecuaciones para determinar las constantes de integración. Sobre todo cuando solo se requiera calcular un solo valor de rotación y/o deflexión.

Método de Greene de Área-Momento

Las ideas iniciales para los dos teoremas de área momento fueron desarrollados inicialmente por Otto Mohr y luego establecidos formalmente por Charles E. Green en 1872. Estos teoremas proporcionan una técnica semigráfica para determinar la pendiente de la curva elástica así como su deflexión debida a la flexión. Son de gran utilidad cuando se usan para resolver problemas de vigas, especialmente aquellas sometidas a una serie de cargas concentradas o que tienen segmentos con diferentes momentos de inercia.

1er Teorema
El enunciado del primer teorema de Área-Momento puede expresarse como: El cambio en la pendiente entre dos puntos cualquiera sobre la curva elástica es igual al área del diagrama M/EI entre esos dos puntos. La formulación matemática correspondiente sería:

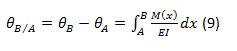
De la cual se desprende que:

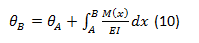
2do Teorema
El enunciado del segundo teorema de Área-Momento puede expresarse como: La deflexión de una tangente a la curva elástica de una viga en un punto B con respecto a una tangente prolongada en otro punto A, es igual al “momento” del Área del Diagrama M(x)/EI entre los dos puntos respecto al punto B donde se busca la deflexión y donde la desviación tB/A va a determinarse. Matemáticamente el momento del Área del Diagrama con respecto a B es igual área de momento entre A y B multiplicada por el centroide de esa área con respecto a B. La formulación matemática correspondiente sería:

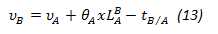
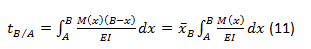
Donde xb es positivo si se mide hacia la derecha y negativo en caso contrario.
Por otro lado si se sabe que:

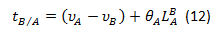
De la cual se desprende que:

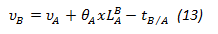
Adicionalmente si se toman como A y B puntos con deflexión conocida, nos queda:

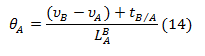
Por lo tanto los pasos que se deben seguir para este procedimiento son los siguientes:
a. Se determina el diagrama de Momento Flector actuante en la viga.
b. Se determinan rotaciones y/o deflexiones iniciales aplicando las condiciones de borde, generalmente entre los apoyos del sistema y la ecuación 14.
c. Con el valor de rotación inicial encontrado se pueden determinar el resto de las rotaciones al aplicar el primer teorema y la ecuación 10.
d. Con la deflexión inicial y las rotaciones encontradas se pueden determinar las deflexiones de los restantes puntos con la ecuación 13.

La principal ventaja de este método, radica en que no es necesario resolver un sistema de ecuaciones y la principal desventaja radica en que solo se puede calcular el valor de la deflexión y/o rotación en un solo punto a la vez. Sin embargo mediante procedimientos de interpolación numérica y con los suficientes puntos, es posible establecer las ecuaciones de rotación y deflexión, sin embargo el procedimiento en forma manual puede resultar muy laborioso.

Método de Mohr o de los Pesos Elásticos y viga Conjugada

Los métodos de los pesos elásticos y viga conjugada fueron inicialmente presentados por Otto Mohr en 1860. En realidad el método de los pesos elásticos es un caso particular del método de la viga conjugada para el caso de vigas simplemente apoyadas. Esencialmente requiere la misma cantidad de cálculos que el método de Greene, sin embargo estos métodos se basan en los principios de la estática y por lo tanto su aplicación es más familiar. El nombre de viga conjugada se refiere al hecho de que los soportes y el sistema de cargas de análisis debe modificarse para determinar las rotaciones y deflexiones actuantes.

En este sentido, los cambios en los soportes de la viga original para conformar la viga conjugada van a depender de las condiciones de borde de la viga original, por ejemplo los apoyos tipo rodillo o bisagra quedan iguales, los apoyos tipo de empotramiento perfecto pasan a ser bordes libre y los bordes libres pasan a ser empotrados perfectos.
Con respecto al sistema de cargas, el sistema de cargas originales de la estructura se reemplaza por el diagrama de momento de la viga. Es decir, la viga conjugada está “cargada” con el diagrama M(x)/EI de la viga real.

Al igual que con el método de Greene, podemos establecer dos teoremas relativos a la viga conjugada; estos son:

1er Teorema
El enunciado del primer teorema del método de la viga conjugada puede expresarse como: La pendiente en un punto cualquiera de la viga real es igual a la fuerza cortante V* en el punto correspondiente en la viga conjugada.
Es decir matemáticamente este teorema puede establecerse como:

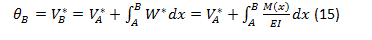
ó

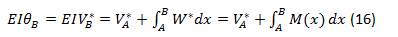
2do Teorema
El enunciado del primer teorema del método de la viga conjugada puede expresarse como: la deflexión o desplazamiento vertical en un punto cualquiera de la viga real es igual al momento en el punto correspondiente en la viga conjugada.

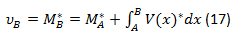
ó

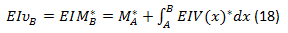
Por lo tanto los pasos que se deben seguir para este procedimiento son los siguientes:
a. Se determina el diagrama de Momento Flector actuante en la viga.
b. Se cambian los soportes de la estructura original por los correspondientes a la viga conjugada
c. Se coloca como “cargas” de la viga conjugada el diagrama de momento obtenido para la viga real, si la forma del diagrama no es de fácil manejo se puede sustituir por una serie de trapecios (mínimo 5 para cada diagrama).
d. Se calculan las “reacciones” de la viga conjugada las cuales corresponderán con las rotaciones y/o deflexiones en esos puntos.
e. Se calculan los diagramas de Corte, por la ecuación 15 o la 16, cuyos valores y diagramas corresponderán a las rotaciones de la viga original.
f. Se calculan los diagramas de Momento, por la ecuación 17 o la 18, cuyos valores y diagramas corresponderán a las deflexiones de la viga original.

La principal ventaja y desventaja de este método son las mismas a la del método de Greene.

Método de la carga Ficticia Unitaria

El método de la carga ficticia unitaria es una aplicación de la ley de conservación de la energía (Trabajo Externo o We = Trabajo Interno o Wi) y del principio del trabajo virtual. El Principio de Trabajo Virtual 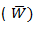es un procedimiento auxiliar que plantea el trabajo ficticio complementario que realizaría un sistema de carga virtuales sobre la deformada de una estructura real, y al unirlo con la ley de conservación de la energía, se tiene:

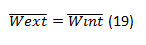
El trabajo externo viene dado por la sumatoria multiplicación de las cargas externas aplicadas por el desplazamiento resultante en la estructura en los puntos de aplicación de las cargas, si la carga es una fuerza vertical el desplazamiento correspondiente es el bajamiento, flecha o deflexión en el punto de aplicación de la fuerza, si la carga es un momento el desplazamiento correspondiente es la rotación que experimenta la viga en ese punto. Como es virtual, el trabajo externo virtual vendrá dado por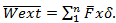

El trabajo interno o más bien energía de deformación interna, viene dado por la sumatoria o la acumulación de los trabajos internos diferenciales que se dan a lo largo de la estructura. El trabajo interno entonces viene dado a partir de la suma de la multiplicación de las fuerzas internas por las deformaciones internas asociadas. En el caso de las vigas, y asumiendo solo efectos de flexión, el trabajo interno resulta de la Integral o suma sobre la longitud de la viga de los momentos internos (corresponde a la fuerza interna) por las deformaciones internas que corresponden a las curvaturas, los cuales se suman o integran a lo largo de la longitud de la viga. Se debe recordar que la curvatura está relacionada con el momento interno a partir de la expresión φ=M/EI. Resumiendo, como es interno y virtual la expresión para el trabajo virtual interno viene dada por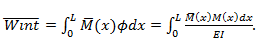

Al sustituir las expresiones de trabajo virtual externos e interno en la ecuación 19, resulta

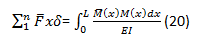
El método de la carga ficticia unitaria, establece que si sobre una viga virtual similar a la real pero con una sola carga virtual aplicada en un punto cualquiera de la viga, se le aplican las cargas de la viga real, por medio de la formulaciones del trabajo virtual es posible determinar el desplazamiento que la viga real tendría en el punto de aplicación de la carga virtual. Es decir si solo se tiene una carga virtual o F ̅ el desplazamiento δ en la viga real en el punto donde F ̅ esta aplicada, se puede obtener a partir de la expresión:

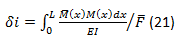
Si además establecemos que 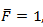, nos queda,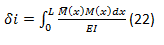

Dónde:
δi = El desplazamiento o rotación que se quiere determinar.
M(x) = La ecuación de momento en la viga real.
M ̅(x)= La ecuación de momento en la viga virtual, la cual está sometida a una sola carga en el punto donde se quiere determinar el desplazamiento. Esta carga es una fuerza vertical si se quiere determinar una flecha y un momento si se quiere determinar una rotación.
EI = Modulo de rigidez a flexión, viene como producto del módulo de Young (E) y de la inercia de la sección transversal (I).

Después de todo lo expuesto, los pasos que se deben seguir para este procedimiento son los siguientes:
a. Se determina el diagrama de Momento Flector actuante en la viga.
b. Se define la viga virtual, aplicando la carga virtual unitaria en el punto donde se quiere determinar la deflexión o rotación. Esta carga debe ser una fuerza vertical si se quiere determinar una flecha y un momento si se quiere determinar una rotación.
c. Se determina el diagrama de Momento Flector actuante en la viga virtual.
d. Se calcula el bajamiento o rotación deseada por medio de la expresión .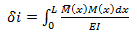
e. La ecuación anterior plantea la integración de la multiplicación de dos polinomios la cual se puede realizar en forma exacta o por medio de algunos de los procedimientos de integración numérica como Suma de Trapecios, Simpson 1/3, Simpson 3/8, Cuadratura de Gauss, entre otros procedimientos.

Al igual que en los métodos de Greene y Mohr, la principal ventaja radica en que no es necesario resolver un sistema de ecuaciones y la principal desventaja radica en que solo se puede calcular el valor de la deflexión y/o rotación en un solo punto a la vez, además de tener que resolver la integral de una multiplicación de polinomio. Sin embargo, si se utilizan procedimientos de integración numérica, es posible reducir en forma sustancial la dificultad de los cálculos. Por otro lado, si las expresiones de momento virtual se dejan en forma genérica, se puede establecer las ecuaciones de rotación y deflexión, sin embargo estos procedimientos en forma manual pueden resultar laboriosos.

Método de Castigliano

Alberto Castigliano, un ingeniero de ferrocarriles italiano, publicó en 1879 un original y elaborado tratado sobre las estructuras estáticamente indeterminadas. En este libro estaban incluidos los dos teoremas que hoy se conocen como teoremas de Castigliano. El primero de ellos, al que generalmente se conoce como teorema de trabajo mínimo, es la base de muchos de los procedimientos posteriores de análisis de estructuras estáticamente indeterminadas. El segundo, proporciona un método muy valioso para el cálculo de las deflexiones, sobre todo ante efectos indirectos como de temperatura, movimientos de soportes y demás, y permitió popularizar los métodos energéticos aunque últimamente su aplicación fue reemplazada por el método de la carga ficticia unitaria. Este segundo teorema será el que expondré a continuación.

2do Teorema de Castigliano
Para toda estructura elástica lineal sujeta a un conjunto determinado de cargas, temperaturas constantes, y apoyos sin desplazamientos la primera derivada parcial de la energía de deformación con respecto a una fuerza en particular, será igual al desplazamiento de esa fuerza en la dirección de aplicación.
Al unir el segundo teorema de Castigliano con los principios del trabajo virtual, nos queda la expresión más conocida para determinar deflexiones por flexión en vigas utilizando los trabajos de castigliano, la cual es:

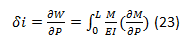
Al igual que para el método de la carga ficticia unitaria, al aplicar el teorema, se debe tener una carga en este caso denominada P en el punto donde se quiere determinar la deflexión y M si se desea una rotación. Después de efectuar las operaciones algebraicas en las expresiones correspondientes se reemplaza en éstas el valor numérico de P o M. Si no se tiene una carga en el punto o en la dirección de la deflexión buscada, se coloca una carga P o M ficticia en la dirección deseada. Después de terminar las operaciones, el valor correcto de P o M (cero) se sustituye en la expresión obtenida.

Después de todo lo expuesto, los pasos que se deben seguir para este procedimiento son los siguientes:
a. A la viga original se le aplica una carga P ó momento M en el punto donde se quiere determinar la deflexión o rotación. En el caso de que exista una carga o Momento esta será reemplazada por el valor genérico de P o M (también se podría dejar la carga original y agregar una carga adicional de valor P o M, la cual al final se debe sustituir por cero).
b. Se determina las ecuaciones de momento para este nuevo sistema de carga.
c. Se determina las derivadas parciales con respecto a la fuerza P o el momento M, de las ecuaciones de momento anteriormente determinadas con respecto a P o M, la expresión de las derivadas parciales resultan iguales a las ecuaciones de momentos obtenidas de una viga sometida solo a la carga P o el momento M, según sea el caso.
d. Se calcula el bajamiento o rotación deseada por medio de la expresión .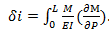
e. Obtenidas las expresiones definitivas para el cálculo de las deflexiones o rotaciones, se sustituye el valor real de la carga P o M en el punto de aplicación donde se quiere determinar la deflexión o la rotación, en el caso de que no exista la carga o se haya tomado como adicional, se debe colocar cero.
f. En el caso de que no se desee resolver la integral de la multiplicación de los polinomios, también se puede tomar como 1 el valor de P o M en las ecuaciones de las derivadas parciales y resolver la integración por medio de algunos de los procedimientos de integración numérica como Suma de Trapecios, Simpson 1/3, Simpson 3/8, Cuadratura de Gauss, entre otros procedimientos.

La principal ventaja y desventaja de este método son las mismas del método de carga ficticia unitaria.

También como esencialmente el problema del calculo de deflexiones y rotaciones en una viga es un problema de ecuaciones diferenciales, se pueden aplicar cualquiera de los métodos establecidos para resolverlas como aplicación de transformadas, series de funciones como la de Fourier, solución numérica de las ecuaciones diferenciales como los método de Euler, Hunt, y de Runge Kutta, entre otras.

Expuestos los métodos y los pasos a seguir en cada uno de los principales métodos de cálculos de deflexiones en vigas, me despido. En un próximo artículo expondré ejemplos de deflexiones de vigas con cada uno de los diferentes métodos.

Espero les haya gustado, si así fue voten y sígueme @davidg83.