Deflections in Beams

Hi friends and dear students I leave an article on the main methods for the calculation of the deflections in beams, then I will upload others with solved and proposed examples.

Methods of Calculation of Deflections in Beams

Introducción

The elements that form a structure are made of materials that deform when loaded. If your deflections exceed permissible values, this can have an impact on the aesthetic appearance of the structures and the materials fixed to these elements can be damaged. For example, a rib or belt that deforms excessively can cause cracks in the gypsum commonly used as a false ceiling or even in concrete and materials used as finishes such as marble or ceramic. On the other hand, a structure should not vibrate or deflate too much to make it look "safe" to its occupants. The calculation of deflections is also essential in the calculation of hyperstatic structures.

The normal practice in Venezuela and in many countries of the world, is to limit the deflections caused by the loads acting (usually the variable or live) to a value lower than L / 360 where L is the length or clear of the stretch of analyzed beam However, these restrictions may change depending on the use and type of the structure.

Over the years several methods have been formulated for the calculation of deflections, which in general are due to the effects of axial force, shear force and momentum. In the particular case of the beams there are no effects of axial force and for the superelevation ratios or H / L ratio (Height / length generally> 10) the effect of the shear deformations can be neglected, therefore most of the methods and procedures formulated to calculate their deflections are based only on bending deformations.

In this order of ideas, in this article we will determine the elastic deflections of beams using the double integration methods or formulated by Henry Navier, geometric methods such as those formulated by Charles Greene and Otto Mohr and Energy methods such as those based on virtual work (originated from Daniel Bernoulli's statements) and in the Castigliano theorem. Each of these methods have advantages and disadvantages that will be exposed when presented.

Elastic Beam Theory

From the works of Euler, Bernoulli and Coulomb, it is obtained that a prismatic beam subjected to pure flexion is flexed in the form of an arc and that, within the elastic range, the curvature of the neutral surface can be expressed from the relation 1 / ρ = M / EI. Where 1 / ρ represents the curvature or angle of the even flat walls of a differential after bending, M the internal bending moment and EI the modulus of flexural rigidity that comes from the multiplication of the Young's modulus (E) and the Inertia of section (I).

Also from the equations of mathematical calculation, the mathematical expression that governs the curvature of an arc is given by:

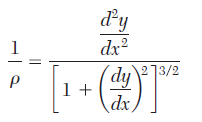(1)
Where, in the case of deflections the variable y represents the deflection or arrow. Therefore, you have to:

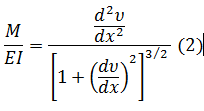
Which represents a non-linear second-order equation. Its solution, ν = f (x), gives the exact shape of the elastic curve only by bending effects. This equation can be approached in an important way considering that dv / dx are small values and its square is even smaller and therefore the denominator expression tends to 1 in almost all cases and therefore the previous expression can be taken as:

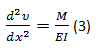
On the other side of this hypothesis, it also appears that the angle that describes the intersection of the planes rotated during bending (dθ) is equal to the length of the arc (ds) between the radius of gyration (ρ), that is:

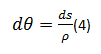
Assuming that dv / dx is practically zero, it is also assumed that ds = dx and therefore the previous expression is:

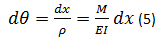
ó

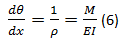
Double integration method

Navier was the first to realize that the equation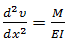
is an ordinary, linear, second order differential equation. Which for a prismatic (those of constant section) can be multiplied both members of the equation by EI and integrate in x again and again, you can write,

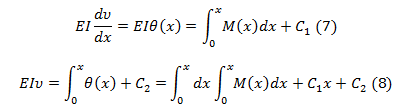
The constants C1 and C2, can be determined by the conditions of edge or border, more precisely, the conditions imposed on the beams by their supports, for example the values C1 and C2 represent the values of the rotation and deflections at the beginning of the beam.

If there are several load conditions in a beam, then two integration constants come out for each section and for its solution, in addition to the edge conditions, continuity conditions will be required both at the level of rotations and deflections. Also in these cases, you can leave the values of rotation and deflection at the ends of each section as a function of C1 and C2 and determine their values with the edge conditions.
Therefore, the steps that must be followed for this procedure are the following:

a. The Flector Moment equation (s) is determined
b. The initial, border and continuity conditions are established in case they are necessary.
c. The equation is integrated again and again to obtain the deflection solution family.
d. The particular solution is obtained by establishing a system of equations with the conditions of edge and continuity or by leaving the extreme values of each section based on the first contants C1 and C2, making use of the conditions of continuity and determining them with the conditions of edge.

The main advantage of the double integration method is that a mathematical expression can be obtained to calculate the deflections and rotations along the whole beam. The main disadvantage lies in the number of operations necessary to solve the system of equations and determine the integration constants. Especially, when it is only required to calculate a only value of rotation or deflection.

Area-Moment Method.

The initial ideas for the two moment area theorems were initially developed by Otto Mohr and then formally established by Charles E. Green in 1872. These theorems provide a semi-graphic technique to determine the slope of the elastic curve as well as its deflection due to bending. They are very useful when used to solve beam problems, especially those subjected to a series of concentrated loads or that have segments with different moments of inertia.

1st Theorem
The statement of the first Area-Moment Theorem can be expressed as: The change in slope between any two points on the elastic curve is equal to the area of the M / EI diagram between those two points. The corresponding mathematical formulation would be:

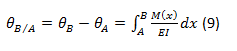
From which it follows that:

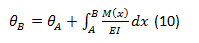
2nd Theorem
The statement of the second Area-Moment theorem can be expressed as: The deflection of a tangent to the elastic curve of a beam at a point B with respect to a prolonged tangent at another point A, is equal to the "moment" of the Area of the Diagram M (x) / EI between the two points with respect to point B where the deflection is sought and where the deviation tB/A will be determined. Mathematically the moment of the Area of the Diagram with respect to B is equal moment area between A and B multiplied by the centroid of that area with respect to B. The corresponding mathematical formulation would be:

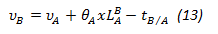
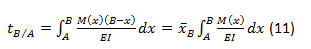
Where xb is positive if measured to the right and negative otherwise.
On the other hand if it is known that:

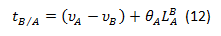
From which it follows that:

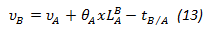
Additionally, if we take as A and B points with known deflection, we have:

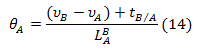
Therefore, the steps that must be followed for this procedure are the following:
a. The Flector Moment diagram acting on the beam is determined.
b. Initial rotations and / or deflections are determined by applying the edge conditions, generally between the supports of the system and equation 14.
c. With the initial rotation value found, the rest of the rotations can be determined by applying the first theorem and equation 10.
d. With the initial deflection and the rotations found, the deflections of the remaining points can be determined with equation 13.

The main advantage of this method is that it is not necessary to solve a system of equations and the main disadvantage is that only the value of the deflection and / or rotation can be calculated in a single point at a time. However, by means of numerical interpolation procedures and with enough points, it is possible to establish the rotation and deflection equations, however the procedure in manual form can be very laborious.

Mohr Method of Elastic Weights and Conjugate Beam

The methods of elastic weights and conjugate beam were initially presented by Otto Mohr in 1860. Actually the elastic weights method is a particular case of the conjugate beam method for the case of simply supported beams. Essentially it requires the same amount of calculations as the Greene method, however these methods are based on the principles of statics and therefore their application is more familiar. The conjugate beam name refers to the fact that supports and the load system of analysis must be modified to determine the rotations and deflections acting.

In this sense, the changes in the supports of the original beam to form the conjugate beam will depend on the conditions of edge of the original beam, for example the supports type roller or hinge remain the same, the props type of embed perfect pass to Be free edges and free edges become perfect recessed.
With respect to the load system, the system of original loads of the structure is replaced by the moment diagram of the beam. That is, the conjugate beam is "loaded" with the diagram M(x)/EI of the real beam.
As with Greene's method, we can establish two theorems concerning the conjugate beam; these are:

1st Theorem
The statement of the first theorem of the conjugate beam method can be expressed as: The slope at any point of the real beam is equal to the shear force V * at the corresponding point in the conjugate beam.
In other words, mathematically, this theorem can be established as:

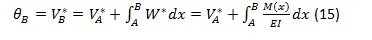
ó

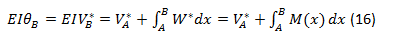
2nd Teorem
The statement of the second theorem of the conjugate beam method can be expressed as: the deflection or vertical displacement at any point of the real beam is equal to the moment at the corresponding point in the conjugate beam.

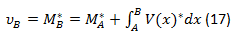
ó

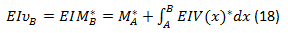
Therefore, the steps that must be followed for this procedure are the following:
a. The Flector Moment diagram acting on the beam is determined.
b. The supports of the original structure are changed by those corresponding to the conjugate beam
c. The diagram of moment obtained for the real beam is placed as "loads" of the conjugate beam, if the shape of the diagram is not easy to use it can be replaced by a series of trapezoids (minimum 5 for each diagram).
d. The "reactions" of the conjugate beam are calculated which will correspond to the rotations and / or deflections in those points.
e. Share diagrams are calculated by equation 15 or 16, whose values and diagrams correspond to the rotations of the original beam.
f. The Moment diagrams are calculated by equation 17 or 18, whose values and diagrams correspond to the deflections of the original beam.

The main advantage and disadvantage of this method are the same as the Greene method.

Unitary Fictitious Load Method

The unit dummy load method is an application of the law of conservation of energy (** External Work or We = Internal Work or Wi **) and the principle of virtual work. The Principle of Virtual Work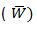 it is an auxiliary procedure that proposes the complementary fictitious work that a virtual loading system would perform on the deformed of a real structure, and when uniting it with the law of conservation of energy, we have:

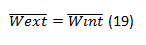
The external work is given by the sum of the multiplication of the ** external loads applied by the resulting displacement ** in the structure at the points of application of the loads, if the load is a vertical force the corresponding displacement is the Deflection or arrow at the point of application of force, if the load is a moment the corresponding displacement is the rotation that the beam undergoes at that point. As it is virtual, the virtual external work will be given by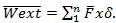

The internal work or rather energy of internal deformation, is given by the summation or the accumulation of the differential internal works that occur along the structure. The internal work is then given from the sum of the multiplication of the ** internal forces by the associated internal deformations**. In the case of beams, and assuming only bending effects, the internal work results from the Integral or sum over the length of the beam of the internal moments (corresponds to the internal force) by the corresponding internal deformations to the curvatures, which are added or integrated along the length of the beam. It must be remembered that the curvature is related to the internal moment from the expression φ = M / EI. In summary, since it is internal and virtual, the expression for internal virtual work is given by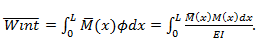
Substituting the external and internal virtual work expressions in equation 19 results in

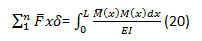
The method of the unit imaginary load establishes that if on a virtual beam similar to the real one but with a single virtual load applied at any point of the beam, the loads of the real beam are applied, by means of the formulations of the Virtual work it is possible to determine the displacement that the real beam would have at the point of application of the virtual load. That is, if you only have a virtual load or F ̅ the displacement δ in the real beam at the point where F ̅ is applied, you can obtain it from the expression:

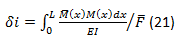
If we also establish that
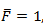, we have left,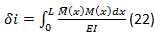

Where:
δi = The displacement or rotation to be determined.
M(x) = The moment equation in the real beam.
M ̅ (x) = The moment equation in the virtual beam, which is subject to a single load at the point where the displacement is to be determined. This load is a vertical force if you want to determine an arrow and a moment if you want to determine a rotation.
EI = Modulus of flexural rigidity, comes as a product of the Young's modulus (E) and the inertia of the cross section (I).
After all the above, the steps that must be followed for this procedure are the following:
a. The Flector Moment diagram acting on the beam is determined.
b. The virtual beam is defined, applying the unit virtual load at the point where the deflection or rotation is to be determined. This load must be a vertical force if you want to determine an arrow and a moment if you want to determine a rotation.
c. The Acting Moment Moment diagram on the virtual beam is determined.
d. The deflection or rotation is calculated by means of the expression! [] (). The above equation proposes the integration of the multiplication of two polynomials which can be done in an exact way or by means of some of the numerical integration procedures like Sum of Trapezoids, Simpson 1/3, Simpson 3/8, Square of Gauss, among other procedures.

As in the Greene and Mohr methods, the main advantage is that it is not necessary to solve a system of equations and the main disadvantage is that you can only calculate the value of the deflection and / or rotation in a single point to the time, in addition to having to solve the integral of a polynomial multiplication. However, if numerical integration procedures are used, it is possible to substantially reduce the difficulty of the calculations. On the other hand, if the expressions of virtual moment are left in generic form, the equations of rotation and deflection can be established, however these procedures in manual form can be laborious.

Method of Castigliano

Alberto Castigliano, an Italian railway engineer, published in 1879 an original and elaborate treatise on statically indeterminate structures. In this book were included the two theorems that today are known as Castigliano's theorems. The first of these, which is generally known as a minimum work theorem, is the basis of many of the later procedures of statically indeterminate structure analysis. The second, provides a very valuable method for the calculation of deflections, especially in the face of indirect effects such as temperature, movement of supports and others, and popularized the energy methods but lately its application was replaced by the method of unitary fictitious load. This second theorem will be the one that I will expose next.

2nd Theorem of Castigliano
For any linear elastic structure subject to a given set of loads, constant temperatures, and bearings without displacements the first partial derivative of the deformation energy with respect to a particular force, will be equal to the displacement of that force in the direction of application.
By joining Castigliano's second theorem with the principles of virtual work, we have the best known expression to determine bending deflections in beams using castigliano works, which is:

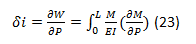
As for the unit imaginary load method, when applying the theorem, one must have a load in this case called P at the point where the deflection is to be determined and M if a rotation is desired. After performing the algebraic operations in the corresponding expressions, the numerical value of P or M is replaced in them. If there is no load in the point or in the direction of the deflection sought, a false charge P or M is placed in the desired address. After finishing the operations, the correct value of P or M (zero) is substituted in the obtained expression.

After all the above, the steps that must be followed for this procedure are the following:
a. A load P or moment M is applied to the original beam at the point where deflection or rotation is to be determined. In case there is a load or Moment this will be replaced by the generic value of P or M (you could also leave the original load and add an additional load of value P or M, which in the end should be replaced by zero) .
b. The moment equations for this new charging system are determined.
c. The partial derivatives are determined with respect to the force P or the moment M, of the moment equations previously determined with respect to P or M, the expression of the partial derivatives are equal to the equations of moments obtained from a beam subjected only to the load P or the moment M, as the case may be.
d. The desired decrease or rotation is calculated by means of the expression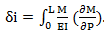
e. Obtained the definitive expressions for the calculation of the deflections or rotations, the real value of the load P or M is substituted in the point of application where deflection or rotation is to be determined, in the case that the load does not exist or have taken as an additional, zero should be placed.
f. In case you do not want to solve the polynomial multiplication integral, you can also take the value of P or M in the equations of the partial derivatives and solve the integration by means of some of the integration procedures. Such as Sum of Trapezoids, Simpson 1/3, Simpson 3/8, Quadrature of Gauss, among other procedures.

The main advantage and disadvantage of this method are the same as the unit dummy loading method.

Also as essentially the problem of the calculation of deflections and rotations in a beam is a problem of differential equations, any of the established methods can be applied to solve them as application of transforms, series of functions such as Fourier, numerical solution of differential equations such as Euler, Heun, Runge Kutta, among others.

Exposed the methods and the steps to follow in each one of the main methods of calculation of deflections in beams, I say goodbye. In a future article I will expose examples of bending deflections with each of the different methods.

I hope you liked it, if so it was voted and follow me @ davidg83.