How to compare two DNA sequences by hand - the Needleman-Wunsch algorithm
First of all, no sane person working in bioinformatics would spend time comparing DNA sequences by hand with all the fast digital tools available (here's one). Still, any bioinformatician would do well to understand the technique, in part because it contains an element of subjectivity.
Two DNA sequences that share a common origin are said to be homologous. It could be the gene for insulin in humans and the one in cattle. The genes are called orthologs when they are both homologous and come from different species. Homologous gene sequences differ, because the ancestral sequence has mutated in different places in the lineages descending from it. The mutation can be a substitution:
AACGT to ACCGT
An insertion:
AACGT to AACCGT
Or a deletion:
AACGT to ACGT
When DNA is transcribed into RNA, it is read in triplets, pieces of three adjacent bases. The three corresponding RNA bases are later translated into an amino acid. Substitutions tend to be the least harmful mutations, because they each affect zero or at most one amino acid. Three-base insertions or deletions are also relatively harmless, because the addition or removal of a triplet means one amino acid more or less in the finished protein (I stress relatively harmless; even substitutions can be lethal if they occur in a bad spot). Insertions or deletions of base numbers not divisible by three are bad news, because they disturb the reading frame of the sequence, potentially affecting all amino acids downstream from the mutation. They are called frameshift mutations and usually lead to the translation of a non-functional protein.
Because of their potential for causing frameshifts, indels (insertions or deletions) are less frequently preserved in the course of evolution than substitutions. When aligning two homologous DNA sequences of unequal length, the occurence of an indel has to be assumed. This is represented by a gap:
A_CGT
AACGT
We may even choose to assume an indel between sequences of the same length, if it makes for a better alignment. But since indels are often severe, their inclusion should be punished. That is, we apply a gap penalty.
There is a multitude of different ways to compare even short DNA sequences. Without an algorithm to locate the best options, the computers of today would not be able to handle even a small fraction of the genetic information currently published. Fortunately, the Needleman-Wunsch algorithm (developed by Saul B. Needleman and Christian D. Wunsch) makes for optimal alignment of large sequences. Short sequences can be aligned by hand. The rest of this post will describe the procedure.
How to run a Needleman-Wunsch algorithm
First, draw a matrix. Each side should be the length of one of the sequences you want to compare, plus one cell. We are going to compare two sequences of 6 and 7 bases, respectively, so we need a 7x8 matrix:
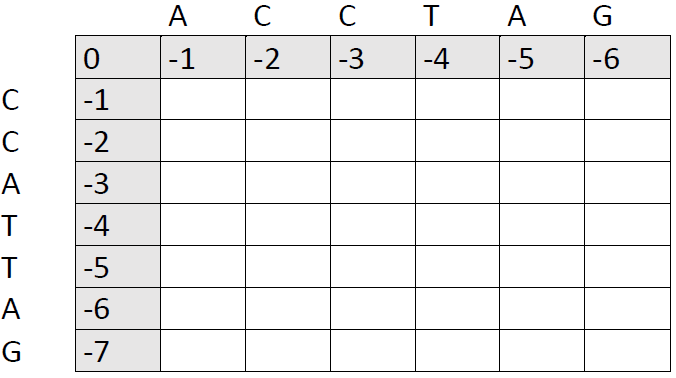
You will notice that I have already filled out part of the matrix. Indeed, this is a bit premature. We first need to decide on a match score, a mismatch score and a gap penalty. This is the subjective part of the algorithm. I have used 1, 0 and -1. If in doubt, one can try to run the same alignment several times with different scores to see how much this affects the final results.
The idea is to start in the upper left corner of the matrix and work your way down the alignment. A diagonal move means that you are simply comparing the next base in sequence 1 to the next base in sequence 2. A horizontal or vertical move signifies the introduction of a gap in, respectively, the vertical and horizontal sequence. Since our gap penalty is -1, every expansion of the gap in the same direction adds -1 to the total score unless we obtain a match.
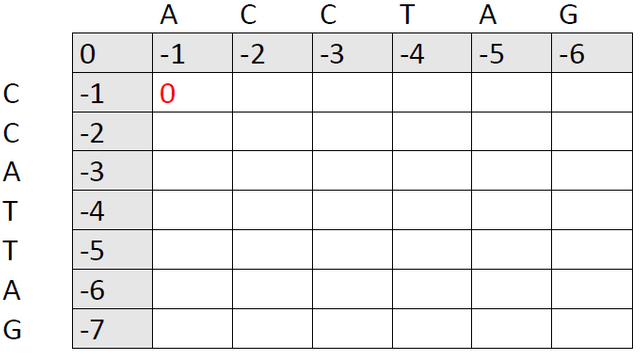
Now, lets attempt to align our first base. We have three options, but the first two are rather silly. We could introduce a gap in sequence 1 and then a gap in sequence 2. Or we could introduce a gap in sequence 2 and then a gap in sequence 1. Or we could just avoid gaps altogether and align the first base in sequence 1 with the first in sequence 2. You might have guessed what I prefer, but take a look at the scores to be sure:
Option 1: -1 + (-1) = -2
Option 2: -1 + (-1) = -2
Option 3: 0
0 > -2. We put 0, because we got a mismatch (A and C). At this point, it's preferable to a gap, so we put a 0 in the matrix.
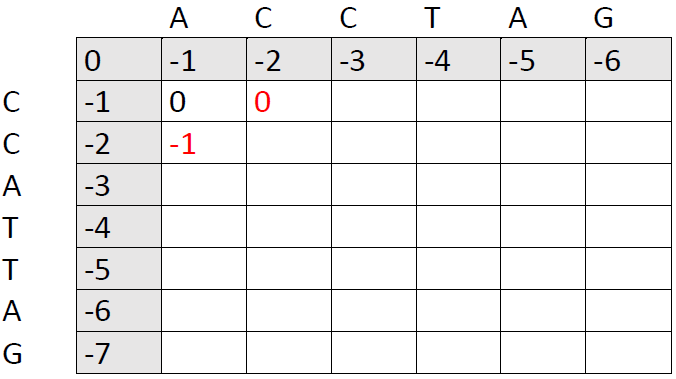
Now, we just need to fill out the rest of the matrix. It's important to put the best option in each cell based on the three cells that precede it to the west, north west and north.
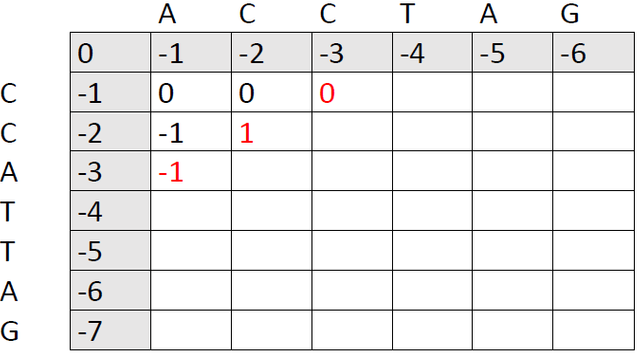
The new 0 was chosen as the best of these three options:
Option 1: Add a gap in sequence CCATTAG by moving right after aligning A and C:
0 [A and C mismatch] + 1 [C and C match] + (-1) [new gap] = 0
Option 2: Add a gap in sequence ACCTAG by moving downwards after aligning A and C:
0 [A and C mismatch] + 0 [A and C mismatch] + (-1) [new gap] = -1
Option 3: Align the second base in ACCTAG with the first base in CCATTAG by moving diagonally after introducing a gap in CCATTAG:
-1 [gap in CCATTAG] + 1 (C and C match) = 0
Option 1 and 3 are equally good and beat option 2, so we put a 0 in the cell.
We continue to add new numbers to the matrix, one slash at a time:
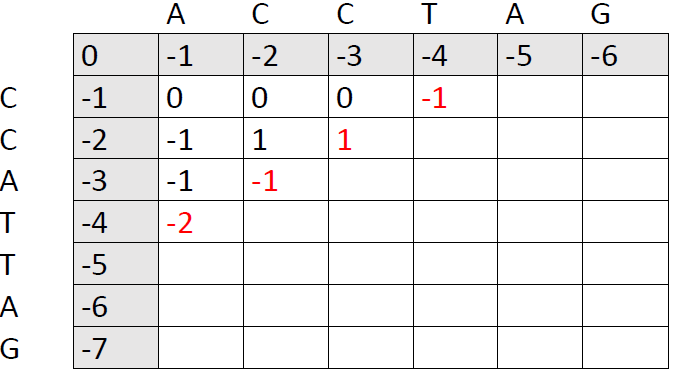
Fast-forward...
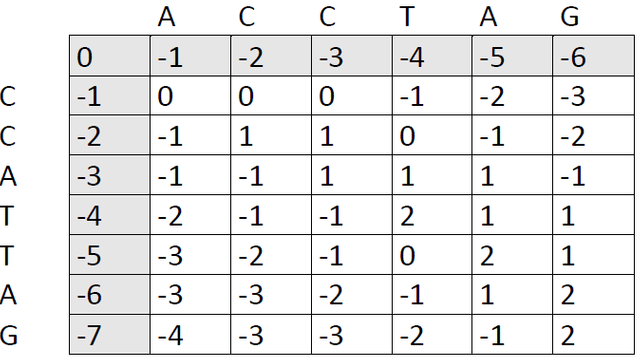
Our final score is the number in the lower right corner, in this case 2. The next step is to trace back through the matrix to see which alignment patterns led to this score. We ask ourselves: Which of the preceding cells could have produced the number 2. There are two options:
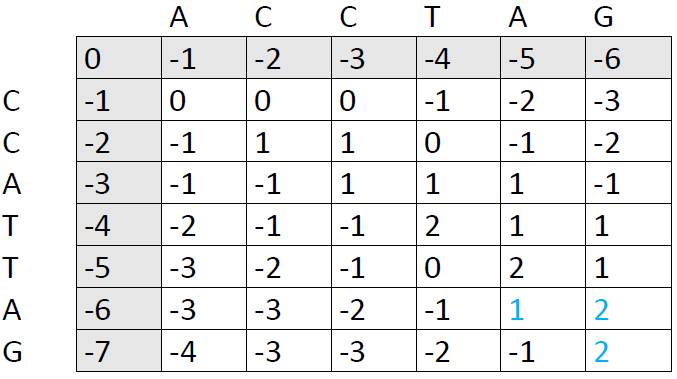
We now follow each path back to the upper left corner. I've used blue color here, because it was faster in Word, but it's more helpful to draw arrows so you can see each individual path right away:
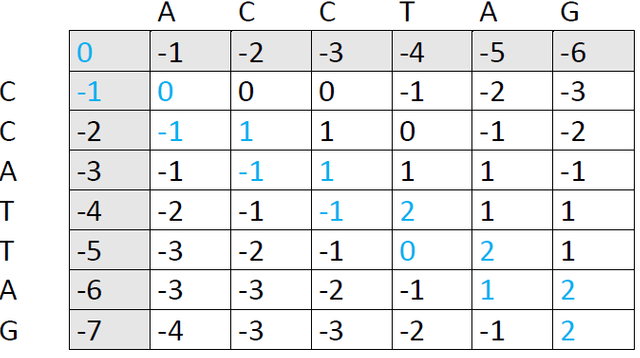
There are three possible paths here, each of them producing an optimal alignment. The first one is:
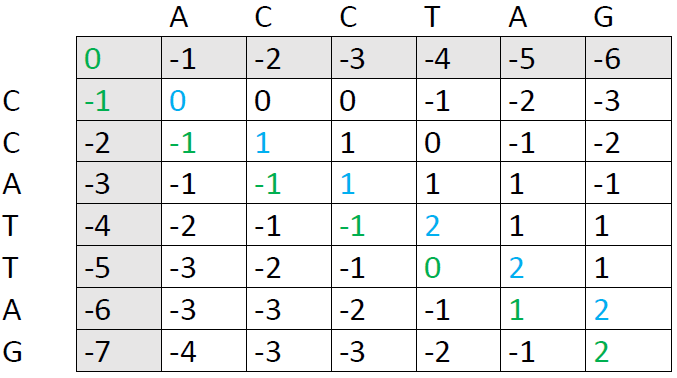
It corresponds to the following alignment:

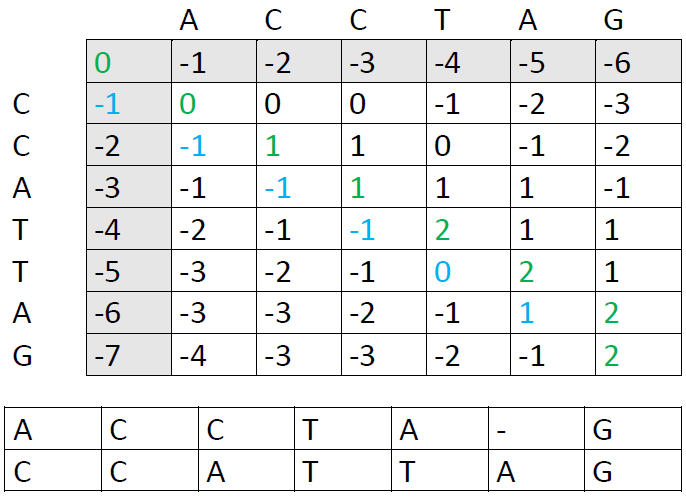
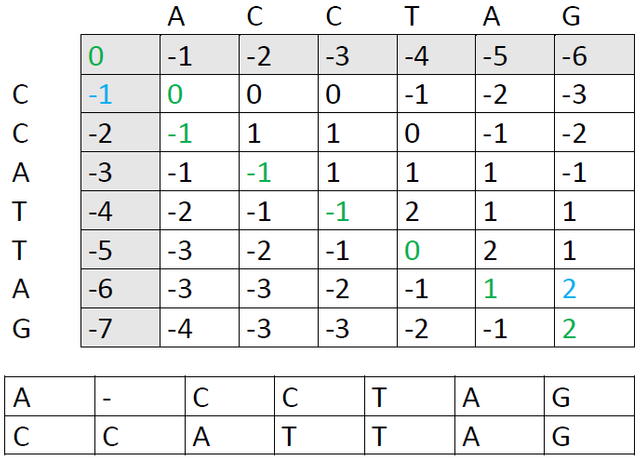
These are the other options:
Book reference
Caroline St. Clair and Jonathan E. Visick (2015): "Exploring Bioinformatics: A Project-based Approach"