Global Navigation Satellite Systems (GNSS) - How does GPS and Satellite Navigation Work?

What is navigation?
It is a field of study that focuses on the process of monitoring and controlling the movement from one place to another. Navigation is relative, and we have to use a coordinate system. We need to also node the coordinates of our potential destinations. Moreover, we also need to know our linear accelerations, linear velocities, linear coordinates and angular acceleration and coordinates (pitch, yaw, roll). That means we need at least 15 parameters for calculation.
Coordinate systems
Inertial Coordinate System (Reference Frame)
- Newton’s law of motion are valid
- Neither rotating, nor accelerating
Earth Centered Inertial Coordinate system
- Orientation of the equatorial plane at 1200 hours UTC, January 2000 – system used by GPS
Earth Centered Earth-Fixed Coordinate System
- X-axis points in the direction of 0 degrees longitude
- Y-axis points to 90 degree E longitude
- The three axes rotate with the earth, and don’t describe directions in inertial space
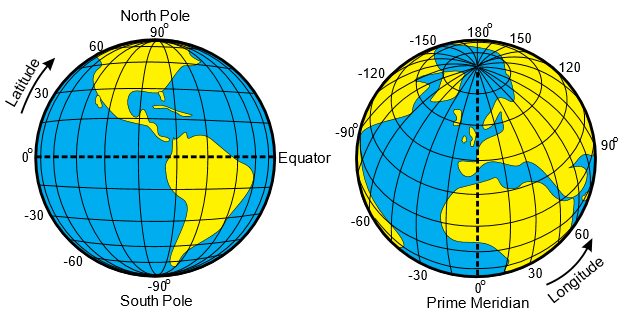
World Geodetic System
- Standard physical model of the Earth, used by GPS
- DOD World Geodetic System 1984 – provides an ellipsoidal model of the Earth that allows enables estimation of the latitude, longitude and height of a GPS receiver
- Uses latitude and longitude to determine location (most widely known)
- Latitude lines run N and S parallel to the equator (N hemisphere > 0, S hemisphere < 0, equator = 0)
- Longitude lines run E and W to the prime meridian (E hemisphere > 0, W hemisphere < 0, prime meridian = 0)
Position determination by GNSS
The time determines the space. How can we determine our location if we know the position of the source which sends a signal to the Earth in a given coordinate system?
We know
- Coordinates of the source
- Exact time at which the signal was sent
We need to
- Measure the time when we receive the signal
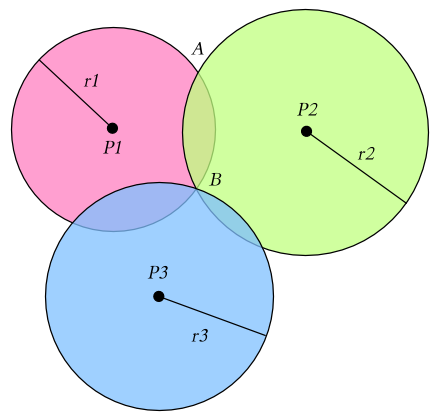
Pinpointing the exact location
- Our location can be anywhere on the periphery of a circle, with the measured distance as radius (see circle 1 below)
- If we use a second source, the target can be at two different locations, and we cannot exactly determine the position (cross section of circles 1 and 2, gives points A and B in the figure below)
- If we have 3 sources, we can EXACTLY determine the location – the cross section of 3 circles has exactly one intersection point, that touches all the circles – in the figure, this is B (this is a trilateration, and enables us to find the location in 2D space)
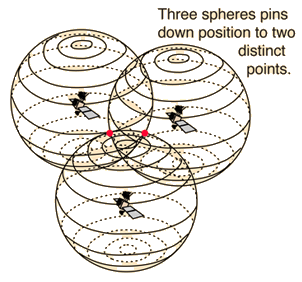
In GNSS
We use satellites, as the entities which send signals. They are placed in the sky, so we need to know their positions in the world geodetic system. In this case, the sent signals are electromagnetic waves. Of course, we also need to find the location in 3D space in this case.
We need to find 3 different unknowns to find out location in the world geodetic system (X, Y, Z). Measuring the time the signals travels from the satellites (X1, Y1, Z1 for satellite 1, …) to the user, we can determine the coordinates.
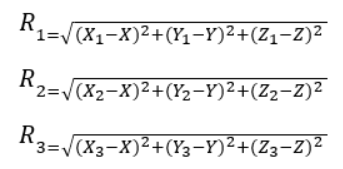
Errors of GNSS
We measure time – travelling of the light, of the electromagnetic wave. The speed of light C = 300 000 km/s and if we have a clock error of our receiver of 1ms, our error in distance measurement will be 300km:
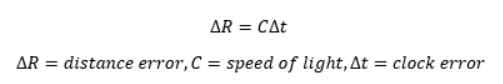
The time error of the clock is constant for all of the satellites – and so is the speed of light, so we can just add the distance error to the previous equations. If we use four satellites we will be able to determine four unknowns and we need to determine ∆t. Therefore, we MUST use at LEAST 4 satellites in practice.
Wow, this is some top notch stuff. It makes me sad when I see top notch posts not getting what they deserve.
Thank you for teaching ! Excellent post !
Hey I like your work so far. In future posts, if you write high quality, scientific posts, or posts that fit within the STEM fields, please feel free to use the #steemSTEM tag for a better chance of bigger upvotes, and join us in the steemstem group on steemit.chat where all the scientists, engineers and so forth come together!
Interesting. Didn't know about this group, thanks for mentioning it. It seems there are a lot of interesting articles there. I will take a more in depth look later when I'll have more time.
great information thanks for educating us
Excellent post, well done @avrdan. Upvoted, resteemed and shared on Linked In. Followed you, too