Banach-Tarski paradox 1+0=2?
The Banach-Tarski paradox is a theorem that is a part of set-theoretic geometry. It raises the questions with whether you can decompose something like a sphere into an infinite number of point sets and them put the points together to make two spheres that are completely identical to the original.

What is the paradox
The Banach-Tarski paradox states that with a solid ball, it is possible for it to be decomposed into an infinite number of disjoint subsets. These subsets that can then be rotated and translated to create two identical copies of the original ball. This can be done with as little as 5 pieces. The reason it's called a paradox is because it says that by dividing a ball into parts then, translating and rotating them with no stretching and or warping of the pieces or adding new ones, you can create two identical balls. This goes against basic geometric concepts. This would seam impossible because you would not be conserving the volume of the ball. This is not the case though because with the of the Banach-Tarski paradox because it is impossible to define the volume of the subsets.
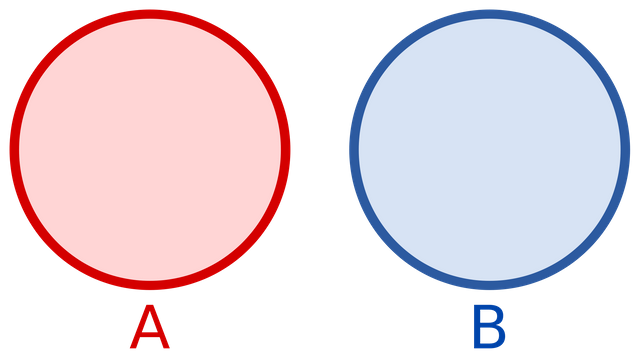
- A disjoint is a set that has nothing in common with another. For example, the sets [1,2,3] , [4,5,6] are disjoint sets. Now [1,2,3], [3,4,5] are not disjoint sets. This is because the sets [1,2,3] and [3,4,5] share a number, 3.
Learning about the paradox
To first understand the Banach-Tarski paradox, you first have to have a grasp of infinity. Infinity is a number greater than any assignable quantity or countable number, or perhaps just a name to describe how many numbers there are. There are different kinds of infinity though. (It is advised to read the bit bellow about infinity, but if you want to cut to the main part of it skip to, The Idea, part.
Infinity:

Countable infinity: A set that has elements that can be put in one-to-one correspondence with the natural numbers set. " In other words, one can count off all elements in the set in such a way that, even though the counting will take forever, you will get to any particular element in a finite amount of time." Math Insight
Uncountable infinity: A set of numbers numbers that contains too many numbers to count. This can be imagined by this example. Try to count all the numbers between 0 and 1. If you say 1, well .1 is also in between and .01 and .0000000001. You cannot possible count all of them. This means that the amount of numbers between 0 and 1 is greater than the amount of whole numbers on the entire endless number line.
To be noted: There are the same amount of even number as there are all even and odd numbers combined. This is because the whole number set is denser than the even number one, but the even numbers can all be paired to a single whole number. For example:
2 4 6 8 10 12 14 16 18 20
1 2 3 4 5 6 7 8 9 10
This is what is called a one-to-one correspondence and it means that both sets are the same size.Hilbert's Hotel: Hilbert's hotel is a famous example of infinity. Imagine that you had a hotel with an infinite number rooms, and every room was booked with somebody in it. Now lets say that somebody comes and asks to have a room. This would mean that every person already in the hotel would shift over one room. If a person leaves, the opposite happens and everybody shifts one room over less than their current number so person in room 2 goes to room 1, and since there are infinite guests, there will be no room left empty. So this means that ∞ -1 = ∞ and ∞ +1 = ∞ .
The Hilbert's Hotel example can also be applied to shapes like circles with every point on the circle being a guest. Also because a circle is irrational being measured by 2π r. This shows that if count every point clockwise going one length of the radius you would never land on the same point making the circle an infinite set. So if you had removed a point on the circle, all you would have to do is rotate the circle over counter clockwise and it would fill every room.

- Hyperwebster: The Hyperwebster is a set of all information and everything that can be made from the 26 letter alphabet. It goes like this. Imagine you set out to make a set of letters starting with A, the it going to AA, then AAA and so on until there is an infinite number of those . After there is an infinte number of those you get to AAB, then AABA, AABAA, until you reach an infinite number of those until AB, then ABA, and ABAA and so on. This patter goes on until you reach the Z's. Which at that point you would have a grand list of infinite information with everything that is and isn't in it. This would contain many many volumes, but it can be simplified. If you took just one of the sets and put it into a volume of itself and named it A. The person that may read it could assume that every set in it starts with, A , thus removing the need to include A in the beginning of each set at all. An if that is done, you would be left with everything you started with but from one single volume.
The Idea
If you take a 3-dimensional object, it can be decomposed into a list like the Hyperwebster. The first part of making this Webster is to give each point on the circle a specific name. So starting from one point you can name every other point using the terms left, right, up and down on two axis that are perpendicular by moving the start point a certain distance, just making sure never to back track. This gives us a list like the Hyperwebster only using the terms: L, R, U, D. So like, L, LL, LLL, and UL, ULL, ULLL, and so on, but you can never have LR because you would end up at the same point that you started at. The number of points that can be made is countable infinite.

Now if you redraw all of the coordinates out on the surface of the sphere starting from a point and name the sphere, you can name each point making a named countably infinite set. If you do this for every point starting with a different direction you can create a countable infinite set that has 4 distinct groups. You may be asking though, but even if you have all the points you will never have enough because the spheres surface has an uncountable infinite amount of points. To resolve this just pick any point that hasn't been defined yet and make it a new starting point, and use every set made previously from it. After doing this to the uncountable infinite points as starting points, you will have identified every single point of the spheres surface a single time, besides the poles of the sphere.
- poles: All the sequences that you identified have 2 points of rotation or poles. This is basically 2 points on the sphere which come back to where they began. For example if you have Left and Right, any sequence with rotations of left or right, the poles are the North and South. The issue though is that multiple sequences lead to the same pole and cane then be named more than one time. To deal with this you just count them out of the sequence and give them a new identification like a color. And because every sequence has two poles, there is a countable infinite number of these different kind of points on the sphere.
Reconstruction:
If you gave every point on the sphere one name and one color: left, right, up, down, poles, starting point, yellow, blue, red, green, pink, purple you can now deconstruct the sphere. Now because the sphere is solid there are more points bellow the surface. But because we counted every point on the surface, each point corresponds to all the points underneath it all the way to the center. Putting the center point aside for now, you can take all the different colors and names and single them out into groups of their own.
If you take the piece named right, it is made from every point ending in a rotation of right. If you rotate that piece left, it will add left to every rotation statement in its sequence cancelling out all the rotations that rotate right but had the left rotation added to it. This leaves us with a new list with all the points ending with up or down, and no rotation which happens to be 3/4 of the original sphere. Now you just add two of the left over sets to make one complete copy. With the remaining 3 sets you can recreate the original sphere.
In the end you are left with two identical spheres from an original sphere by adding nothing!
If you got this far, thank you for reading and I hope you enjoyed this article.
Sources:
www.math.hmc.edu/funfacts/ffiles/30001.1-3-8.shtml#
en.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox
en.wikipedia.org/wiki/Uncountable_set
www.math.illinois.edu/~ajh/347.summer14/cardinality.pdf
mathinsight.org/definition/countably_infinite
upload.wikimedia.org/wikipedia/commons/thumb/7/7e/Sphere_wireframe_10deg_6r.svg/2000px-Sphere_wireframe_10deg_6r.svg.png
upload.wikimedia.org/wikipedia/commons/thumb/d/df/Disjunkte_Mengen.svg/2000px-Disjunkte_Mengen.svg.png
www.publicdomainpictures.net/pictures/60000/nahled/green-infinity-2.jpg
pixabay.com/static/uploads/photo/2015/07/18/04/48/hotel-850020_960_720.jpg upload.wikimedia.org/wikipedia/commons/0/07/Sphere_and_Ball.png
upload.wikimedia.org/wikipedia/commons/thumb/1/1a/Brosen_windrose.svg/2000px-Brosen_windrose.svg.png
Great sharing, great explanations! Thanks!