The Game of Life: A Fun Game and Interesting Mathematical Model of Biological Life
In 1970, British mathematician John Conway invented "The Game of Life,"which became increasingly popular throughout the nineteen seventiesamong math enthusiasts.
What made this game so very peculiar (and popular)? It could be neither won nor lost. It was not competative. In fact, it was a zero player game which, in a sense, played itself!
All that was needed for a person to play The Game of Life was asimple sheet of graph paper and a pencil (with an eraser). Today it isfar easier (and just as fascinating) to play the game using one of themany online versions (such as this particularly wonderful one found at math.com), but the principles remain the same.
The only variable involved in The Game of Life is the beginning state. The player colors in a certain number of squares ("cells"), creating any desired pattern - then the game takes over.
The Rules of the Game
Once the game's user has created a desired pattern, they must follow step by step through the rules of the game:
A colored cell is known as a "live" cell, where an empty cell is known as a "dead" cell.
1) An empty cell can come to live through the process of "birth." Itcan do this only if it is surrounded by at least three live cells. Sowhen the game begins, the player must look at the pattern they havecreated and determine whether or not there are any dead cells which canbe given birth by their live neighbors.
2) A live cell can be killed due either to overcrowding orloneliness. Overcrowding happens when it is surrounded by four or moreother live cells, whereas loneliness occurs when it is surrounded by less than two live cells.
3) The ideal state, in which a cell remains permanently alive, isthat in which a cell is surrounded by only two or three neighbors.
The Game's Results
While by simply looking at the rules The Game of Life may not soundparticularly interesting or exciting, it can truly become a ratheraddicting activitity, especially thanks to the simple online versions.It is absolutely astonishing to create a seemingly random pattern (or acarefully thought out one) and seeing what sort of unexpected phenomenaresult.
The Game of Life can result in one of three ways:
1) After a number of "turns" the cells reach a state of equilibrium and stop growing or die entirely.
2) The growth and change never stops - the "organism" keeps growing and changing endlessly without repetition.
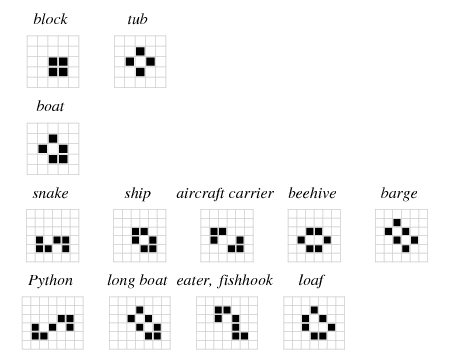
3) A repeating pattern develops, many of which have been discoveredand even given names by enthusiasts of the game (several examples can be found here).
Though only these three results are possible, the varieties withinthem are absolutely endless, especially considering that just a single"block" of just nine squares can result in over 500 variations!
While The Game of Life may seem like just a somewhat entertaining(and potentiall addictive) diversion from life, it has actually led,believe it or not, to some real mathematical breakthroughs.
Games, programs, and algorithms such as these, which are set inmotion and then operate under very specific principles and rules inorder to "see what happens" are known as cellular automatae, and while Conway's creation of rules which mimick the actual forces ofbiological life (death, birth, overcrowding, etc.), more advancedexamples of cellular automatae truly have proven useful increating models which are meant to provide insight into the growth,expansion and evolution of biological systems and populations.
A rather fun bit of mathematics, then, has made its way into a numberof scientific areas, and because it has only developed and becomepopularized within the past four decades, there remain many morediscoveries to be made here, to be certain.
Sources:
oscilators are the best part of game of life

I haven't heard about the "game of life" since forever. I remember my brother had it. So funny. Great post.
Congratulations @alv, this post is the seventh most rewarded post (based on pending payouts) in the last 12 hours written by a Dust account holder (accounts that hold between 0 and 0.01 Mega Vests). The total number of posts by Dust account holders during this period was 3291 and the total pending payments to posts in this category was $763.89. To see the full list of highest paid posts across all accounts categories, click here.
If you do not wish to receive these messages in future, please reply stop to this comment.