Is it possible to receive and transmit information faster than light?
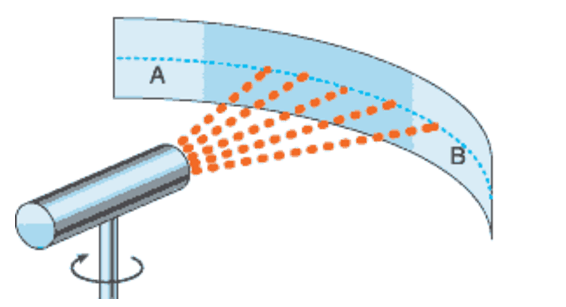
If we take, for example, a flashlight (or, say, a laser that gives a narrow beam) and quickly describe the arc in the air, the linear speed of the spot of the "bunny" in the sky will increase with distance and at a sufficiently large distance will exceed the speed of light. The light spot moves between points A and B at a superluminal speed, but this will not be a signal transfer from point A to point B, since the light spot does not carry any information about point A. However, everything changes if the Holographic Principle works.
Let's imagine an unusual gyroscope in which a spherical rotor levitation in a vacuum and it can be rotated in any direction under the control of the computer around one fixed point - the center of mass. If in a normal gyroscope the rotor makes one revolution around one axis in one cycle, then in an unusual gyroscope, the rotor produces a complete revolution around the three axes. All the points of the rotor and, hence, the elements of its mass, produce coherent oscillations. Antinodes and nodes of accelerations from an interference pattern of six identical groups, which are directed along six fixed Cartesian coordinate axes. We have six groups of rotational accelerations, which according to the Holographic Principle are projected on six opposite sides of the holographic screen of the Universe without loss of information.
These six groups of accelerations are analogs of our light spot. We can move these groups of "bunnies" in pairs on a holographic screen, but now they are represented by the information itself, which moves without limit by the distance and speed of light. For this, it is sufficient to measure entropy force, which will be applied to the center of mass of the rotor of an unusual gyroscope. This uncompensated entropy force, which is applied to the center of projections and arises as a result of the interaction of entropy gradients caused by the acceleration of the rotor mass elements and the temperature gradients on the holographic screen.
where Fentr is the entropy force ΔT is the temperature gradient, ΔS is the entropy gradient associated with the accelerations during the displacement of the rotor mass elements.
Thus, the task of moving and retrieving information faster than the speed of light can be solved in an unusual gyroscope. Today we need to find the possibility of prototyping an unusual gyroscope.
If there are intelligent civilizations in the universe, they will use this communication channel. What do you think, friends?