Computation Contest #7 [2 SBI]
Here you can solve interesting problems using whatever programming language you like. Also you will earn SBI and sometimes STEM by doing so.
Also you might learn new things by doing so.
The tasks will be rather hard to solve without a programmable computer and some programming skills, but if you want to add a few million numbers by hand or similar, I would still give you the reward.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Rules
No upvote, No resteem, No follow required!
I will give the prize randomly to those who solved the problem.
If two pieces of code are to closely related I might consider the later of them as copied which results in no prize for that person.
You have 4 days to solve it.
Even though this is about computation I will also accept algebraic solutions if you find one.
In order to get accepted you need to somehow attach your code.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Problem
This time the problem is about performance:
I want you to find two different way of approximating π using a computer.
Measure for each of the methods how much time is needed to get it correct to the nth digit ranging n from 0 to 10. 0 meaning that the result is 3.xxx . The result from 10 should be included.
Graph the result.
Compare the time of both methods.
Also take a look at how the time changes compared to the number of digits.
And then tell me which one you would use for
- approximating π to a few digits(10-50)
- approximating π to a lot digit(a lot more than 100).
in a performance critical application.
If there already have been other entries before yours, you have to use at least one unique technique of approximating pi. There are infinitely many different ways to approximate π, so that rule shouldn't make it impossible to join.
If you don't know enough techniques, feel free to ask.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
To everyone who already participated in a past contest, come back today and try a new problem(tell me if you don't want to be tagged):
@crokkon @kaeserotor @ninahaskin @portalmine @tonimontana
In case no one gets a result(which I doubt), I will give away the prize to the person who makes the most constructive description why the problem is too hard in your opinion.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
@contrabourdon sponsors my contests with 2 STEEM weekly.
You can support him by using a witness vote on untersatz, so he can further support this and other contests.
the entry time is prolonged by 1 week.
Hi @quantumdeveloper I find this simple method based on integral calculation.
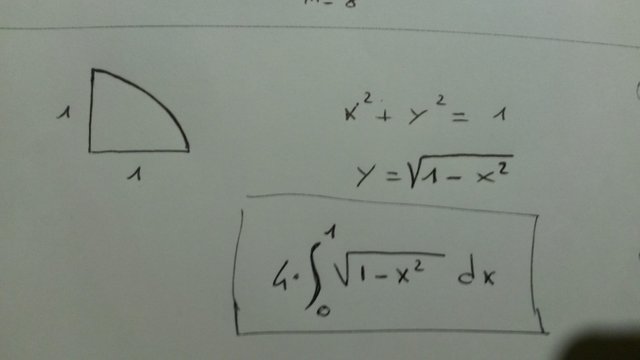
We know that the area of a circle is exactly π if the radius is 1.
And the equation of this circumference is: x^2 + y^2 = 1
So for x positive (x from 0 to 1) : y = sqrt(1-x^2)
I considered a quarter of circumference and calculate its area with an integral, then multiplied the result by 4.
I made a short script on Python, here is it the code (calcola means calculate)
The variable n represents the number of intervals in which I divided the x asses from 0 to 1.
And here it is the calculation
So with 10 milions of intervals I found π correct up to the sixth digit....not enough!!
This method is very slow...I don't recommend it for large calculation
If I find time I will try with another method. A geometrical one!
Bye bye
Don't forget to graph the time you actually need to get this precision.
ok sure, I changed a little bit the code ( I don't know why I make this stupid error ), defining dx as a fix number, so now it is a bit faster, but not so much. :)
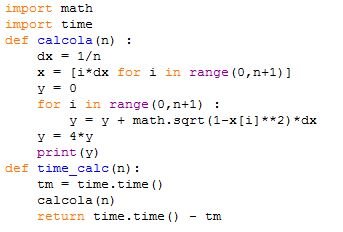
And I add a function to calculate the time.
Now I arrived to the 7nt decimal digit correct. (below the approximation there is the time in seconds)
And the "graph" is:
x axis : correct digit
y axis : time
Obviously it has an exponential shape, and for sure Python is not indicate to make calculations.
That's me again :)
I made an improvement on my code, changing the method to calculate the integral.
I used the trapezoidal method, and now I got the precision to the 10nt digital digit in less time! (23 seconds)
Now I wanna try another method.