Computation Contest #4 [2 SBI]
Here you can solve interesting problems using whatever programming language you like. Also you will earn SBI and sometimes STEM by doing so.
Also you might learn new things by doing so.
The tasks will be rather hard to solve without a programmable computer and some programming skills, but if you want to add a few million numbers by hand or similar, I would still give you the reward.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Rules
No upvote, No resteem, No follow required!
I will give the prize randomly to those who solved the problem.
If two pieces of code are to closely related I might consider the later of them as copied which results in no prize for that person.
You have 4 days to solve it.
Even though this is about computation I will also accept algebraic solutions if you find one.
In order to get accepted you need to somehow attach your code.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Problem
In math there are some functions that cannot be integrated using algebra like this:
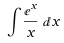
In cases like that you might need your computer to do that.
You can do that by dividing the function into small almost constant portions and summing them all up.
Use this technique to integrate above function in the interval [1/x, x] where x is your current reputation.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
To everyone who already participated in a past contest, come back today and try a new problem(tell me if you don't want to be tagged):
@crokkon @kaeserotor @tonimontana
In case no one gets a result(which I doubt), I will give away the prize to the person who makes the most constructive description why the problem is too hard in your opinion.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
@contrabourdon sponsors my contests with 2 STEEM weekly.
You can support him by using a witness vote on untersatz, so he can further support this and other contests.
So the idea here is to approximate the function in some way in small steps. I used rectangles, triangles would be fine too. You calculate the area of each rectangle and sum them all up to get the area under e^(x)/x within the given intervall. I slowly decreased the step size because I wasn't sure how much my PC could handle.
My reputation is currently 57, and the code gave a result of 1.0156373595307505e+23. This is in good accordance with wolfram alpha (1.015643...e+23), a deviation shows up 5 digits behind the comma. You can improve this with more computation power or time.
.