Bild Referenz: https://commons.wikimedia.org/wiki/File:The_C_Programming_Language_logo.svg

Intro

    Hallo, ich bin's @drifter2! Der heutige Artikel ist an meinem englischen Artikel "C Function Comparison" basiert. Wir werden heute darüber reden wie man Funktionen vergleichen kann, indem man dessen Ausführungszeit vergleicht oder die Anzahl an Berechnungen die ausgeführt werden. Dadurch könnt dir dann besser einschätzen ob eine gewisse Änderung die Effizienz des Algorithmus oder der Implementation verbessert hat, oder generell zwei verschiedene Algorithmen für die selbe Aufgabe (oder das selbe Problem) vergleichen. Also dann fangen wir dann mal direkt an!

---

Ausführungszeit berechnen

    Wenn man in C mit Zeit arbeiten will, muss mit die "time.h" Bibliothek importieren. Die gibt uns Zugriff auf viele Funktionen die mit Zeit zu tun haben. Um die Ausführungszeit zu berechnen werden wie die jetzige Zeit in "Clock Ticks" vor und nach der Ausführung abspeichern und danach die Differenz in Sekunden berechnen.

    Dazu müssen wir 2 Variablen des Datentyps clock_t erstellen, die wir z. B. 'start' und 'ende' nennen können. Zusätzlich brauchen wir eine double Variable (z. B. a_zeit) die die Zeit in Sekunden vom Start bis zum Ende abspeichern wird. Die jetzige Zeit in "Clock Ticks" kann sehr leicht mit der Funktion clock() erfasst werden, welche eine Variable des Datentyps clock_t zurückgibt. Die eigentliche Ausführungszeit ist danach nicht nur eine Subtraktion zwischen 'ende' und 'start', sondern wir müssen auch mit der Konstante "CLOCKS_PER_SEC" dividieren, welche die Anzahl an "Clock Ticks per Sekunde" enthält. Diese Konstante ist per CPU anders.

Wenn man also die Ausführungszeit berechnen will macht man folgendes:

clock_t start, ende;

double a_zeit;

start = clock();

// Funktion ausfuehren

ende = clock();

a_zeit = (double)(end - start)/CLOCKS_PER_SEC;

---

Wie man etwas beim ausführen messt (generell)

    Handelt es sich um eine Iterative Funktion (nicht Rekursiv) oder generell eine Funktion die keine anderen Funktionen ausführt, muss man nur eine Variable definieren die die Anzahl an dem was man berechnen will abspeichert. Diese Berechnung (oder auch Berechnungen, wenn es sich um mehr handelt) kann man dann sehr leicht am Ende bei der Konsole ausgeben oder wieder zurückgeben. Wenn die Funktion bereits was anderes zurückgibt, könnte man diese Berechnung auch durch einen der Parameter zurückgeben, genau wie wir bei den Stapel-Warteschlangen Aufgaben gemacht hatten.

    Sagen wir jetzt mal wir haben eine Rekursive Funktion. Bei dieser könnten wir eine Globale Variable definieren die dann bei jeden Aufruf der Funktion erreichbar ist. Das ist die leichte Lösung! Was mann sonst noch so machen könnte ist z. B. die Berechnung zu dem vorherigen Aufruf zurückzugeben, und das direkt (return-Anweisung) oder wieder mal mit Hilfe von den Parametern. Eine andere sehr interessante Lösung ist das wir die Variable statisch (static) in der Funktion definieren. Dadurch ändert sich der Wert dieser Variable dann nicht bei den verschiedenen Ausführungen der selben Funktion, bei der diese deklariert wurde. Also wird diese dann bei dem ersten Aufruf z. B auf '0' initialisiert und dann bei jedem anderen Aufruf inkrementiert, ohne das diese erneut auf '0' gesetzt wird. Die Variable wird erst "verloren gehen", wenn es sich um den letzen Aufruf der Funktion handelt

---

Vergleichsbeispiele

Funktionen mit Ausführungszeit vergleichen:

   Sagen wir mal wir wollen zwei verschiedene Implementationen dem Sortier-Algorithmus "InsertionSort" vergleichen. Die erste ist eine Iterative und die zweite eine Rekursive Lösung. Um das zu machen werden wir hier die Ausführungszeit vergleichen.

Die Iterative InsertionSort Funktion sieht wie folgend aus:

void insertionSort(int arr[], int n)

{

   int i, j, key;

   for (i = 1; i < n; i++)

   {

       key = arr[i];

       j = i-1;

       while (j >= 0 && arr[j] > key)

       {

           arr[j+1] = arr[j];

           j = j-1;

       }

       arr[j+1] = key;

   }

}

Die Rekursive Funktion ist wie folgend:

void insertionSortRecursive(int arr[], int n)

{

    if (n <= 1)

        return;

    insertionSortRecursive(arr, n-1);

    int last = arr[n-1];

    int j = n-2;

    while (j >= 0 && arr[j] > last)

    {

        arr[j+1] = arr[j];

        j--;

    }

    arr[j+1] = last;

}

    Sagen wir mal wir reden über N = 20000 Elemente (#define N 20000). Damit beide Implementationen mit dem selben Feld vergleicht werden, werden wir zwei Felder definieren und bei mit den selben zufälligen Nummern füllen.

Das sieht wie folgend aus:

int A[N], B[N];

int i;

for(i = 0; i < N; i++){

	B[i] = A[i] = 1 + rand()%1000;

}

      Danach definieren wir erstmal die "Zeit-Variablen" und können dann die Funktionen sehr leicht mit der Ausführungszeit vergleichen. All das sieht wie folgend aus:

clock_t start, ende;

double a_zeit;

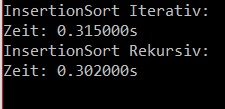
printf("InsertionSort Iterativ:\n");

start = clock();

insertionSort(A, N);

ende = clock();

a_zeit = (double)(ende-start)/CLOCKS_PER_SEC;	

printf("Zeit: %fs\n", a_zeit);

printf("InsertionSort Recursiv:\n");

start = clock();

insertionSortRecursive(B, N);

ende = clock();

a_zeit = (double)(ende-start)/CLOCKS_PER_SEC;

printf("Zeit: %fs\n", a_zeit);

Bei meinen Rechner kommt z. B. folgende Ausgabe:

Ihr könnt den Code bei dem folgenden Link in pastebin runterladen:

https://pastebin.com/gm2ynyKN

Funktionen mit Anzahl an Berechnungen vergleichen:

    Sagen wir jetzt mal wir wollen zwei verschiedene Implementation des Algorithmus für die Berechnung von  größten gemeinsamen Teiler (ggT - gcd auf Engisch) vergleichen. Der erste ist der normale Rekursive Euklid Algorithmus und der zweite eine Andere Lösung, welche aufeinanderfolgende Ganzzahlen vergleicht (consecutive integer checking algorithm auf Englisch). Dieses mal werden wir die Anzahl an modulo-Berechnungen vergleichen.

     Der Rekursive Algorithmus (Euklid) wird eine Statische Variable enthalten und die Operationen bei dem letzten Aufruf dann bei der Konsole ausgeben. Das sieht wie folgend aus:

void gcd(int m, int n){ // Euklid Algorithmus

    int r;

    static int calc_num = 0; // modulo zaehler

    if(n == 0){

        // ausdrucken

	printf("GCD: %d\n", m);

	printf("Calculations: %d\n", calc_num);

	calc_num = 0; // zaehler zuruecksetzen

	return;

    }

    r = m % n;

    calc_num++; // zaehler inkrementieren

    gcd(n, r);

}

    Die Iterative Lösung kann diese Anzahl ganz leicht in einer normalen Variable abspeichern und am Ende aller Iterationen dann ausgeben. Der Code sieht wie folgend aus:

void gcd2(int m, int n){ // consecutive integer checking algorithm

    int t;

    int calc_num = 0; // modulo zaehler

    if(m < n){

	t = m;

    }

    else{

	t = n;

    }

    while(t > 0){

	calc_num++; // zaehler inkrementieren

	if(m % t == 0){

		calc_num++; // zaehler inkrementieren

		if(n % t == 0){

			printf("GCD: %d\n", t);

			printf("Calculations: %d\n", calc_num);

			return;

		}

	}

	t--;

    }

}

     Die Zahlen 'm' und 'n' werden zufällig generiert und dann als Parameter bei beiden Funktionen abgegeben. Da sich diese Zahlen bei der Ausführung nicht ändern, braucht man hier nicht zwei "gleiche" definieren. Die main() Funktion sieht wie folgend aus:

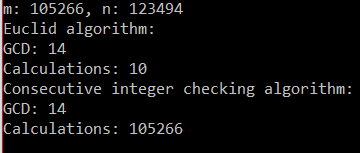
int main(){	

    srand(time(NULL));	

    int m = 100000 + rand() % (200000 - 100000 + 1);

    int n = 100000 + rand() % (200000 - 100000 + 1);

    printf("m: %d, n: %d\n", m, n);

    printf("Euclid algorithm:\n");		

    gcd(m, n);

    printf("Consecutive integer checking algorithm:\n");

    gcd2(m, n);

    return 0;

}

Eine Ausführung kann z. B. wie folgend aussehen:

Der Code kann beim folgenden Link runtergeladen werden:

https://pastebin.com/EFsdqREw

---

Referenzen:

1. https://steemit.com/programming/@drifter1/programming-c-function-comparison

     Der Artikel ist zu 90% eine Übersetzung von meinen englischen Artikel, aber enthält ein paar mehr Informationen. Generell ist alles in diesem Artikel viel besser geordnet und repräsentiert.

---

Vorherige Artikel

Grundlagen 

Einführung -> Programmiersprachen, die Sprache C, Anfänger Programme

Felder ->  Felder, Felder in C, Erweiterung des Anfänger Programms

Zeiger, Zeichenketten und Dateien -> Zeiger, Zeichenketten, Dateiverarbeitung, Beispielprogramm

Dynamische Speicherzuordnung -> Dynamischer Speicher, Speicherzuweisung in C, Beispielprogramm 

Strukturen und Switch Case -> Switch Case Anweisung, Strukturen, Beispielprogramm

Funktionen und Variable-Gueltigkeitsbereich -> Funktionen, Variable Gueltigkeitsbereich

Datenstrukturen

Rekursive Algorithmen -> Rekursion, Rekursion in C, Algorithmen Beispiele

Verkettete Listen -> Datenstrukturen generell Verkettete Liste, Implementation in C (mit Operationen/Funktionen), komplettes Beispielprogramm

Binäre Suchbäume -> Baum Datenstruktur generell, Binärer Baum, Binärer Suchbaum, Implementation in C-Sprache (mit Operationen/Funktionen), komplettes Beispielprogramm

Warteschlangen implementiert mit Feldern -> Warteschlange als Datenstruktur, Implementation einer Warteschlange mit Feldern in C-Sprache, komplettes Beispielprogramm

Stapel implementiert mit Feldern -> Stapel als Datenstruktur,  Implementation eines Stapels mit Feldern in C-Sprache, komplettes Beispielprogramm

Warteschlangen und Stapel implementiert mit Verketteten Listen -> Liste, Warteschlange und Stapel mit Liste implementieren in C-Sprache.

Fortgeschrittene Listen und Warteschlangen -> Doppelt verkettete Listen (mit Implementation), Zirkuläre Listen, Vorrangwarteschlange (mit Implementation)

Fortgeschrittene Bäume -> Βinärer Suchbaum (Zusammenfassung),  AVL-Baum (mit Implementation), Rot-Schwarz (ohne Code) und 2-3-4 Bäume (ohne Code)

Stapel-Warteschlangen Übungsaufgabe mit Dynamischen Feldern -> Aufgabenbeschreibung, Lösung-Implementation in C (zutiefst) und Vollständiges Programm mit Ausführungsbeispiel

Stapel-Warteschlangen Übungsaufgabe mit Verketteten Listen -> Aufgabenbeschreibung, Lösung-Implementation in C (zutiefst) und Vollständiges Programm mit Ausführungsbeispiel

---

Schlusswort

    Und das war's dann auch schon mit dem heutigen Artikel und ich hoffe euch hat dieser Artikel gefallen. Bei den nächsten zwei Artikeln werden wir über Hashtabellen (Hashtables auf Englisch) reden.

Keep on drifting! ;)