Data compression - a problem which has got quite a long history.
Existing data compression algorithms can be divided into two great classes – with and without a loss.
Algorithms with losses are commonly used for compressing images and audio. These algorithms can achieve greater compression ratios due to selective loss of quality. However, by definition, it is impossible to restore the original data from the compressed results.

Lossless compression algorithms are used to reduce the data size and work so that it is possible to restore the data exactly as it was before compression. They are used in communications, archiving programs and some algorithms for compression of audio and graphic information.

We would talk about the lossless compression algorithms.

---

The basic principle of data compression algorithms is based on the fact that in any file that contains non-random data, the information is partially repeated. Using statistical mathematical models we can determine the likelihood of recurrence of a certain combination of symbols. After that, you can create codes for the selected phrases and assign the shortest codes to the most frequently repeated phrases.

Run-length encoding (RLE)

The most famous simple approach and information lossless compression algorithm - a Run Length Encoding - RLE.

The essence of the methods of this approach is to replace the chain or series of repetitive sequences of bytes with an encoding byte and the counter of the number of its repetitions.

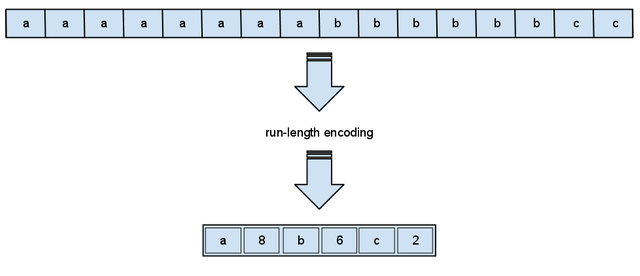
The first byte indicates how many times to repeat the next byte

If the first byte is 00, then it is followed by a counter showing how many unduplicated data should be after it.
These methods are generally efficient enough for compressing raster graphic images (BMP, PCX, TIF, GIF), as they contain a lot of long series of repeated sequences of bytes.

The disadvantage of this method is that RLE compression ratio is quite low.

Arithmetic coding

Arithmetic coding is a method that allows packing the input alphabet symbols without loss, provided that the distribution of frequencies of known symbols are the most optimal, as the theoretical limit of the compression ratio is reached.

Estimated required the sequence of symbols compression by arithmetic coding is considered as some binary fraction of the interval [0, 1). The result of compression is represented as a sequence of binary digits from the record of this fraction.

The idea of the method consists of the following: the source code is seen as a record of this fraction, where each input symbol is the "symbol" with a weight proportional to the probability of its occurrence. This explains the interval corresponding to the minimum and the maximum probability of occurrence of a symbol in the flow.

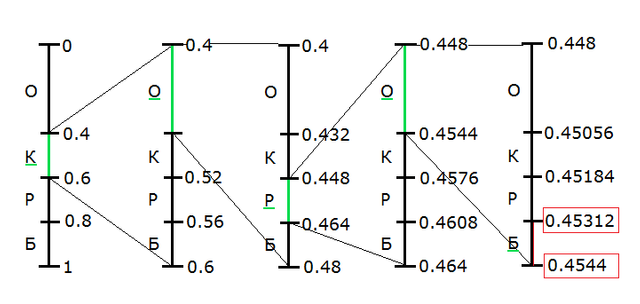
The essence of the algorithm is as follows: each word in the input alphabet corresponds to the sub-interval of the interval [0, 1) and the empty word corresponds to the entire interval [0, 1). Upon receipt of each subsequent symbol, the interval is reduced with the choice of the part that corresponds to the new symbol. The code is an interval isolated after processing of all its symbols, the binary representation of any point of this range, and the length of the resulting interval is proportional to the probability of occurrence of the encoded string.

Lempel-Ziv-Welch - LZW

This algorithm has a high speed of the packaging and unpacking, quite modest memory requirements and a simple hardware implementation.

The disadvantage - low compression ratio as compared with the two-step coding scheme.

Suppose that we have a dictionary that stores the text string containing 2 to 8 thousand numbered slots. We write rows in the first 256 slots, consisting of a single symbol, which number is equal to the number of the slot.

The algorithm scans the input flow, dividing it by string and adding new slot at the end of the dictionary. Let’s read a few symbols in the string s in the dictionary and find a string t - the longest prefix s.

Suppose it is found in slot n. We derive the number n to the output flow, move the pointer of the input flow to the length (t) of symbols forward and add a new slot to the dictionary, containing a string t + c, where c - another symbol on the inlet (immediately after the t). The algorithm converts the flow of symbols at the input into the flow of indices of output dictionary.

In the practical implementation of the algorithm, it should be noted that any slot of the dictionary, except the first ones that contain one-symbol chains, keeps a copy of some other slot to which one character is assigned. Because of this, you can use a simple list structure with a single connection.

Two-step coding. Lempel-Ziv

A much greater degree of compression can be achieved by separation of the input repetitive chains - blocks, and coding of links on these chains with the construction of a hash table from the first to n-th level.

The method consists of the following: packer constantly keeps a certain amount of processed last symbols in the buffer. As the input flow processes newly received symbols fall into the end of the buffer, shifting the preceding symbols and displacing the oldest.

The size of this buffer, that is also called sliding dictionary vary in different implementations of coding systems.

Then, after the construction of a hash table algorithm allocates (by searching in the dictionary) the longest initial substring of the input flow, coinciding with one of the substrings in the dictionary, and outputs the pair (length, distance), where the length - length found in the dictionary of the substring, and distance - the distance from it to the front substring.

---

So we come to the two-stage encoding scheme - the most effective from currently used ones. When implementing this method, consistent output of both flows into a single file need to be achieved. This problem is usually solved by alternately recording of the codes of symbols from two flows.

References: 1

Follow me, to learn more about popular science, math and technologies

With Love,
Kate

Image credit: 1, 2, 3, 4, 5