Theorema egregium i rozmaitości.

Ten artykuł jest powiązany z artykułem o geometriach nieeuklidesowych. Zapraszam zatem najpierw do przeczytania tego drugiego dla lepszego zrozumienia tematu. Artykuł dostępny tutaj:
Theorema egregium

Po osiągnięciach matematyków w dziedzinie geometrii nieeuklidesowych przyszedł czas na uwieńczenie ich pracy. Carl Friedrich Gauss w 1827 roku udowodnił swoje twierdzenie wyborne (theorema egregium). Twierdzenie dotyczące powierzchni dwuwymiarowych, które przetarło szlak do dziedzin tak obszernych i autonomicznych, że nie sposób dzisiaj przebrnąć przez nie wszystkie w ciągu jednego życia. Wykazał on, że:
Niepoprawnym z mojej strony byłoby pozostawienie tego bez komentarza, a zatem spróbujmy zrozumieć twierdzenie wyborne nieco głębiej. Mówiąc o krzywiźnie, która jest niezmiennicza mamy na myśli taką, która jest taka sama w każdym punkcie zakrzywionej powierzchni. Przykładem powierzchni o stałej krzywiźnie jest płaska powierzchnia lub sfera. Krzywizna płaskiej powierzchni jest zerowa, sfery natomiast dodatnia. Chyba każdy conajmniej raz w życiu spoglądał na mapę świata. Jeżeli nie, to jest ona przedstawiona na obrazku poniżej.
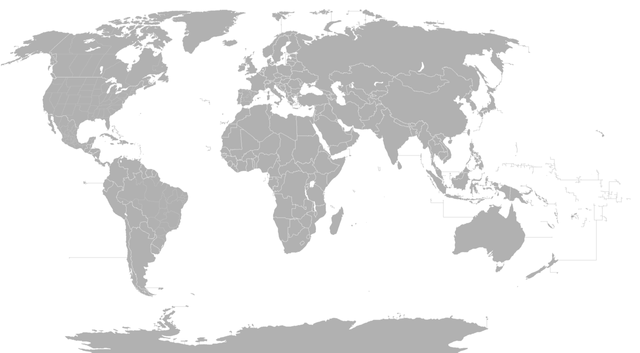
Charakterystyczną cechą mapy świata jest to, że jest ona przedstawiona na powierzchni o zerowej krzywiźnie (płaskiej). Wiemy jednak, że mapa ta odwzorowuje naszą planetę, która w przybliżeniu jest kulą. Aby ująć problem ściślej powinniśmy powiedzieć, że mapa świata jest odwzorowaniem brzegu kuli, która jest naszą planetą (brzeg kuli to sfera). Czy zatem płaska mapa świata jest wiarygodnym odwzorowaniem naszej planety? Gauss i jego theorema egregium mówi nam stanowcze nie! Nie da się odwzorować sfery na płaską powierzchnię zachowując przy tym odległości między punktami, ponieważ krzywizna sfery jest inna niż krzywizna płaskiej powierzchni! W topologii powiedzielibyśmy, że płaska powierzchnia nie jest homeomorficzna ze sferą. Nie istnieje ciągłe przekształcenie jednego w drugie (musimy rozerwać sferę, aby odległości były zachowane, a w topologii jest to niedopuszczalne). Konsekwencje tego faktu są takie, że nasze mapy świata są bardzo niedokładne. Jedyne dokładne odwzorowanie mapy na płaszczyźnie przedstawione zostało na obrazku poniżej.
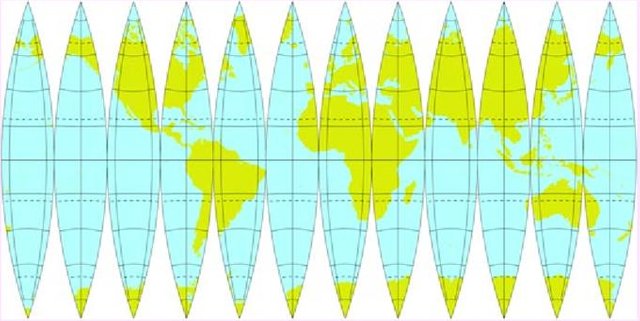
Nie jest to jednak koniec. Twierdzenie wyborne to dopiero początek. Gauss publikując swoje wnioski nie był świadom tego, że jego praca utoruje drogę teorii, która w sposób absolutny zmieniła sposób patrzenia na geometrie, przyczyniła się do powstania geometrii różniczkowej i dała podstawy pod współczesną kosmologię i ogólną teorię względności. Ahh... Jakie musiało być jego odczucie, gdy uświadomił sobie, że dokonał tego jego własny uczeń.
Geometria Riemannowska

Theorema egregium uświadomiła matematykom jeszcze jedną ciekawą rzecz. Okazuje się, że możemy opisywać własności geometryczne powierzchni tylko i wyłącznie za pomocą współrzędnych krzywoliniowych. Oznacza to, że aby opisać w pełni trójwymiarowy obiekt nie musimy odwoływać się do trójwymiarowej przestrzeni, w której ten obiekt jest zanurzony. W 1854 roku Bernhard Riemann wygłasza wykład O hipotezach leżących u podstaw geometrii i burzy dotychczas panujące przekonania. Uogólnia on teorię swojego mentora na przestrzenie o wielu wymiarach, które nazwał rozmaitościami. Okazuje się zatem, że możemy opisywać obiekty n-wymiarowe odwołując się tylko i wyłącznie do obiektów (n-1)-wymiarowych. Teoria rozmaitości wprowadza nowy rodzaj myślenia o obiektach topologicznych, uogólniając przy tym odkryte wcześniej geometrię eliptyczną i hiperboliczną.
Rozmaitość
Przykłady są ważne. Tym razem jednak zacznę od historyjki.
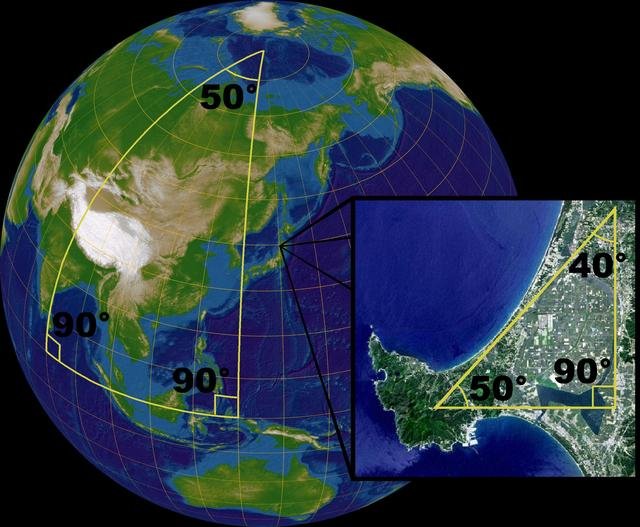
Rozmaitością nazywamy przestrzeń topologiczną, która lokalnie przejawia własności przestrzeni euklidesowej. Innymi słowy bliskie otoczenie dowolnego punktu rozmaitości możemy sukcesywnie opisywać geometrią Euklidesa. Globalnie natomiast jest ona zakrzywiona i geometria Euklidesa nie spełnia swojego zadania. Do globalnego opisu rozmaitości potrzebna jest nam geometria nieeuklidesowa. W topologii powiedzielibyśmy że otoczenie dowolnego punktu n-wymiarowej rozmaitości jest homeomorficzne z n-wymiarową przestrzenią euklidesową (istnieje ciągłe odwzorowanie otoczenia w przestrzeń euklidesową).
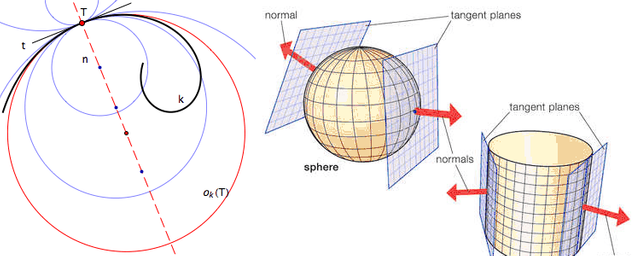
Najprostszym rodzajem rozmaitości są rozmaitości jednowymiarowe. Jest nią na przykład okrąg, czy elipsa. Jeżeli przybliżymy wystarczająco krzywą, która tworzy okrąg zauważymy, że jest ona prostą. Okrąg zatem globalnie jest zakrzywiony, lecz lokalnie przejawia geometrie euklidesową. Następnie mamy takie obiekty jak sfera, czy torus, które są przykładami rozmaitości dwuwymiarowych. Nazywamy je powierzchniami. Gdy przybliżymy powierzchnie sfery, zauważymy że powierzchnia ta jest płaska. Sfera zatem globalnie jest zakrzywiona, lecz lokalnie przejawia własności geometrii euklidesowej. Przypomnijmy sobie teraz mapę świata. Wiemy już, że sfera (brzeg kuli) jest dwuwymiarową rozmaitością. Wiemy również, że otoczenie dowolnego punktu sfery jest euklidesowe. Możemy zatem odwzorować otoczenie wybranego przez nas punktu sfery (w przypadku Ziemi może to być jakieś miasto) na płaską powierzchnię.
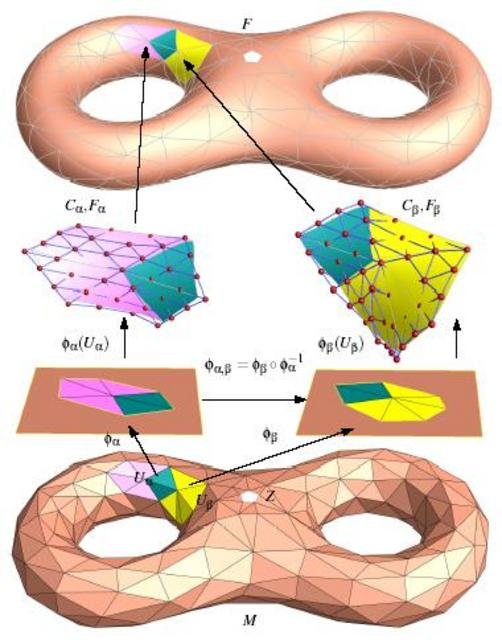
Dla przykładu jeżeli mamy pewien czterowymiarowy obiekt (trójwymiarową rozmaitość), to aby odwzorować ją na przestrzeni euklidesowej potrzebujemy map trójwymiarowych, które utworzą trójwymiarowy atlas. Arcytrudne zadanie dla wyobraźni.
Dodatek
Teoria rozmaitości pozwala nam na opis skomplikowanych struktur za pomocą przestrzeni euklidesowych, co znacznie ułatwia problem. Albert Einstein użył jej w swojej ogólnej teorii względności do opisu zakrzywienia czasoprzestrzeni. Czasoprzestrzeń w której przyszło nam żyć to w języku matematyki tak zwana rozmaitość riemannowska, a ściślej rozmaitość różniczkowa, która posiada własność umożliwiającą nam wykonywanie na niej działań takich jak różniczkowanie, czy całkowanie.
Dziękuje za poświęcenie uwagi. Pozdrawiam!
Źródła zdjęć: 1 2 3 4 5 6 7 8 9 10 11
Kolejny fenomenalny artykuł. Aż nie chce się wierzyć, że piszesz to dzień w dzień po nocach. Dzięki!
I w pracy.
Resteem'owalem, mam nadzieje, ze nie masz nic przeciwko :)
Nie ma problemu :D