Ciąg Fibonacciego
Ciąg Fibonacciego to podział danego segmentu na dwie części, dzięki czemu stosunek dłuższej do krótszej długości jest taki sam, jak całej długości do dłuższej części. Sekwencję tę opisał włoski matematyk Leonardo z Pizy ( zwany Fibonaccim ).
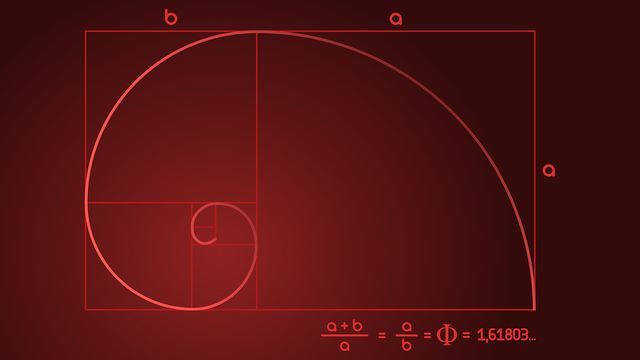)
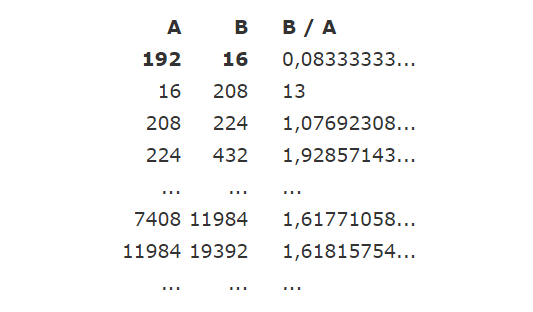
Kiedy podzielimy dwie kolejne liczby w sekwencji Fibonacciego, stosunek tych liczb zawsze będzie taki sam. Wynik wynosi w przybliżeniu 1,618. Im większe liczby dzielimy, tym większe jest nasze przybliżenie. Działa to również wtedy, gdy wybieramy dwie losowe liczby całkowite rozpoczynające ciąg, takie jak przykładowo 192 i 16.
Otrzymujemy następującą sekwencję 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, ...
Liczbę tą nazywamy złotą, była ona już znana starożytnym Grekom i jest oznaczana Grecką literą „Fi” - Φ
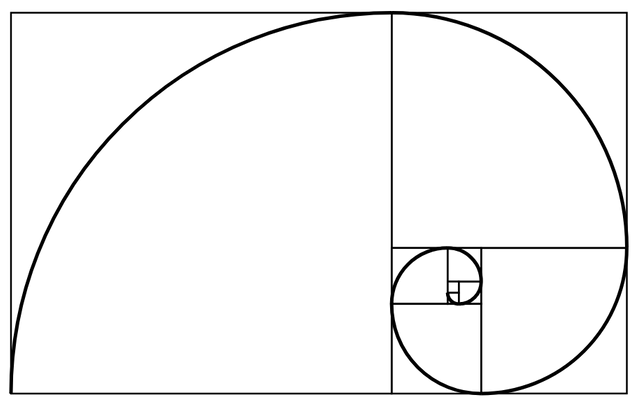
Matematyka tworzy świat, a jej odniesienia można znaleźć wszędzie wokół nas, na każdym kroku. To samo dotyczy liczb Fibonacciego. Formę graficzną tej sekwencji nazywamy Złotą spiralą. Charakterystyczną cechą Złotej spirali jest to, że co 90 ° jej szerokość zwiększa się (lub zmniejsza), a stosunki boków kolejnych kwadratów są równe Φ.
)
Trójkąt Pascala jest matematyczną kombinacją liczb w postaci tablicy. Po bokach trójkąta znajdują się cyfry 1, a pozostałe są uformowane jako suma dwóch bezpośrednio nad nimi. Liczby stojące w n-tym rzędzie to kolejne stosunki dwumianowe Newtona. W tym zapisie możemy również zaobserwować występowanie liczb Fibonacciego.
Możemy to zauważyć, sumując liczby ukazane na poniższej grafice:

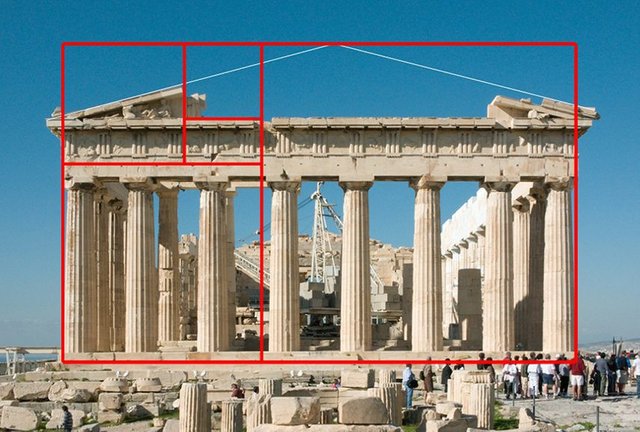
Liczba ta ma również niezwykłe walory estetyczne. Starożytni architekci wykorzystali go do budowy takich budynków jak Partenon. Próbowali łączyć ze sobą jak najwięcej elementów wpasowujących się w dany podział. Działanie takie miało na celu dążenie do uzyskania ideału.
Warto zaznaczyć, że proporcje budowy ciała człowieka posiadają podobieństwa do Złotej spirali. Sztandarowym przykładem tutaj jest stosunek wysokości osoby do długości od stóp do pępka lub stosunek odległości między ramieniem i palcem oraz między łokciem a czubkiem palców. Złote proporcje zachowują nawet spirale naszego DNA. Cząsteczka DNA mierzy 34 jednostki długości do 21 jednostek szerokości dla każdej sekcji podwójnej helisy. Występowanie Złotej Liczby w konstrukcji człowieka, a także w naturze, jest zjawiskiem niezwykłym.
Przykłady takie wskazują na istnienie jakiejś wyższej reguły.
W przeważającej większości optymalnie rozwinięty kwiat bez mutacji i deformacji zawsze ma pewną liczbę płatków będących liczbą Fibonacciego. Zgodnie z zasadami złotego podziału przeprowadzany jest również cały proces wzrostu roślin. Przykładami takich roślin mogą być: słoneczniki, szyszki, stokrotki czy ananasy.
Jeśli ponumerujemy gałęzie zgodnie z wysokością, na której wyrosły, okaże się, że liczba gałęzi sąsiadujących pionowo to liczba Fibonacciego, a ponadto liczba gałęzi między gałęziami pionowymi jest również tą liczbą. Zasada filotaksji spiralnej ma również swoje miejsce w świecie roślin, w którym rosnące liście nie przesłaniają się wzajemnie.
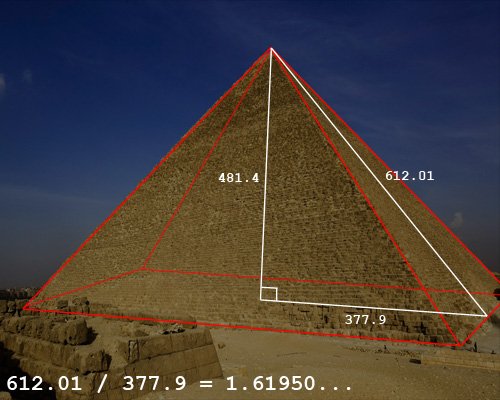
Z tej zasady korzystali również Egipcjanie przy tworzeniu piramid. Ściana boczna piramidy podzielona przez połowę podstawy daje nam przybliżoną liczbę „Fi”.
Można również odróżnić wiele różnych przykładów w sztuce, w tym obrazy: Mona Lisa, Ostatnia wieczerza, Narodziny Wenus czy Marmurowa Rzeźba Wenus z Milo. W dzisiejszych czasach zależności te można znaleźć w logach znanych marek, takich jak:
- Apple
- Toyota
- Pepsi
Zasady sekwencji Fibonacciego i złotej liczby można również znaleźć w świecie muzyki. Związki między poszczególnymi dźwiękami w muzyce opierają się właśnie na matematycznych prawach harmonii, a dokładniej na złotym współczynniku. Zakres słyszalnych dźwięków sięga od 32 do 73700 drgań na sekundę. Dźwięki w zakresie 60-33000 oscylacji mają charakter muzyczny a, odległości pomiędzy dwoma dźwiękami nazywane są interwałami.
Najbardziej przyjemne dla ucha są oparte na liczbie „Fi”.
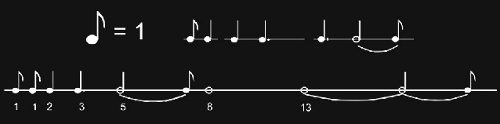
Partytura muzyczna słynnego kanonu D-dur Pachelbela jest skonstruowana według liczb Fibonacciego, a jej odbicie można znaleźć w wielu utworach współczesnej muzyki, na przykład:
- Green Day - Basket Case
- U2 - With or Without You
- Bob Marley - No Woman No Cry
- The Beatles - Let It Be
Ponadto większość sonat Amadeusza Mozarta została podzielona na dwie części dokładnie zgodnie ze złotym podziałem, z tej zasady korzystał również Antonio Stradivarius.
Istnieje wiele innych odniesień, w których istnieje ta zależność podziału według ciągu Fibonacciego. Być może absurdalne może być szukanie wszędzie zasad i zależności sekwencji Fibonacciego, ale fakty mówią same za siebie. Trzeba przyznać, że wiele rzeczy zachowuje zasady Złotego podziału w otaczającym nas świecie.
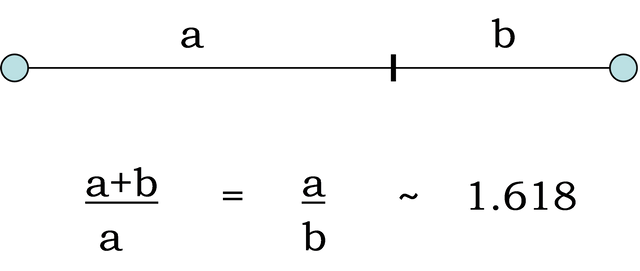

!tipuvote 2 :)
This post is supported by @tipU upvote funded by @cardboard :)
@tipU voting service + profit sharing tokens | For investors.
Twój post został podbity głosem @sp-group-up oraz głosami osób podpiętych pod nasz "TRAIL" o łącznej mocy ~0.17$. Zasady otrzymywania głosu z traila @sp-group-up znajdziesz w ostatnim raporcie tygodniowym z działalności @sp-group, w zakładce PROJEKTY.
@michalx2008x
Chcesz nas bliżej poznać? Porozmawiać? A może chcesz do nas dołączyć? Zapraszamy na nasz czat: https://discord.gg/rcvWrAD