Problem deficytu Śmierdzieli u Indian z plemienia Natchez

Statystyka w służbie naukom społecznym
Przeczytałem ostatnio książkę „Matematyka w czasach współczesnych”, istotnym jest tutaj fakt, że rok wydania tej książki to 1966. Na pierwszy rzut oka tytułowe określenie współczesnych może okazać się archaiczne, jednakże zawartość tej książki mówi co innego. Okazuje się na przykład, że próby zamodelowania biologicznego neuronu sięgają właśnie tamtych czasów. Książka zawiera także problemy natury ogólnej, stanowiące podporę dla omawianych działów matematyki. Nie wspomniałem o autorach i koncepcji – książka ta jest zbiorem artykułów z Scientific American, sygnowanych znanymi nazwiskami ówczesnego naukowego świata – choć należy wspomnieć, że głównie jednak poruszamy się po matematycznych rewirach. I tak oto autorem pierwszego artykułu jest Richard Courant, kolejne nazwiska to: Edward Moore, Morris Kline, mamy także fizyka Freemana Dyson’a. W zbiorze zawierającym 11 artykułów mamy dwóch Polaków, co samo przez się świadczy o szczeblu polskiej matematyki. Stanisław Ulam i Marek Kac podjęli następujące tematy: sztuczna inteligencja oraz prawdopodobieństwo. Znajdują się tam także artykuły opisujące pole działań matematyki w naukach fizycznych, biologicznych i społecznych. I na tym ostatnim – napisanym przez Richarda Stone’a – na chwilę się zatrzymajmy. Jak nietrudno się domyślić, nauki społeczne upodobały sobie statystykę.

I choć wielu matematyków nią gardzi, traktując jak piąte koło u wozu, to jednak wciąż statystyka pozostaje pod jurysdykcją Królowej Nauk. Choć pozbawiona elegancji i polotu, posiada instrumenty dające nam namacalne informacje. Choć brak w niej twierdzeń i teorii, które zmieniły oblicze świata, wydaje się być taka swojska, ogólnodostępna. Wszak policzenie ilości masła z jednego masłolota i uzależnienie tych danych od szerokości torów w różnych państwach jest w zasięgu niemal każdej osoby. W ten sposób otrzymamy ciekawą zależność albo brak jakiejkolwiek. Richard Stone przywołuje przypadek Indian z plemienia Natchez, którzy niegdyś zamieszkiwali basen rzeki Missisipi. Korzysta jednak z głębszej analizy, nie posługując się tylko suchymi danymi. Problem możemy sprowadzić do problemu teorioliczbowego, którego centrum tkwi w ciągach uzależniających przyrosty danych grup klasowych w kolejnych generacjach.

System zawierania małżeństw u Natchezów
Społeczność Indian była podzielona na dwie klasy: arystokratów i proletariuszy. Arystokraci dzielili się jeszcze na trzy podgrupy ze Słońcami na szczycie, niżej byli Szlachetni, a stawkę możnowładców zamykali Szanowni. Na samym dole hierarchii społecznej byli proletariusze zwani Śmierdzielami. W plemieniu Natchez panowały nadzwyczaj ciekawe prawa odnośnie zawierania małżeństw, mianowicie: przynajmniej jeden partner w każdym małżeństwie – mąż lub żona – musiał być Śmierdzielem. Dziecko urodzone przez matkę-arystokratkę miało rangę matki, jednakże w przypadku, gdy matka pochodziła z klasy Śmierdzieli, a ojciec miał wyższą rangę – dziecko dziedziczyło rangę o jeden stopień niższą. Przykładowo: dziecko urodzone w związku ojca-Śmierdziela i matki-Słońca, ojca-Śmierdziela i matki-Szlachetnej, ojca-Śmierdziela i matki-Szanownej, było odpowiednio: Słońcem, Szlachetnym lub Szanownym. Natomiast dziecko z związku matki-Śmierdziela i ojca-Słońca, matki-Śmierdziela i ojca-Szlachetnego, matki-Śmierdziela i ojca-Szanownego było odpowiednio: Szlachetnym, Szanownym, Śmierdzielem. Na samym dole drabiny społecznej, oboje rodzice Śmierdziele mieli potomstwo Śmierdzieli.
Plemię Natchez już nie istnieje, pozostaje jednak ciekawa kwestia przeanalizowania systemu społecznego określonego w tak złożony sposób. Koniecznym jest stworzenie pakietu założeń, bez których nawet nie zaczniemy analizy.
Mianowicie:
- Każdy członek plemienia Natchez wstępował w związek małżeński tylko jeden raz.
- W każdym małżeństwie rodziła się średnio dwójka dzieci: chłopiec i dziewczynka.
- Ilość populacji wyjściowej i jej rozłożenie na dane klasy przyjmuję z literatury [1]
| - | Populacja wyjściowa | I generacja | II generacja | III generacja | IV generacja | V generacja |
|---|---|---|---|---|---|---|
| Słońce (S) | 10 | 10 | 10 | 10 | 10 | 10 |
| Szlachetny (N) | 20 | 30 | 40 | 50 | 60 | 70 |
| Szanowny (H) | 40 | 60 | 90 | 130 | 180 | 240 |
| Razem | 70 | 100 | 140 | 190 | 250 | 320 |
| Śmierdziel | 500 | 470 | 430 | 380 | 320 | 250 |
| Razem | 570 | 570 | 570 | 570 | 570 | 570 |
| - | - | - | - | - | - | - |
| - | G | G+1 | G+2 | G+3 | G+4 | G+5 |
| Słońce | S | S | S | S | S | S |
| Szlachetny | N | N+S | N+2S | N+3S | N+4S | N+5S |
| Szanowny | H | H+N | H+2N+S | H+3N+3S | H+4N+6S | H+5N+10S |
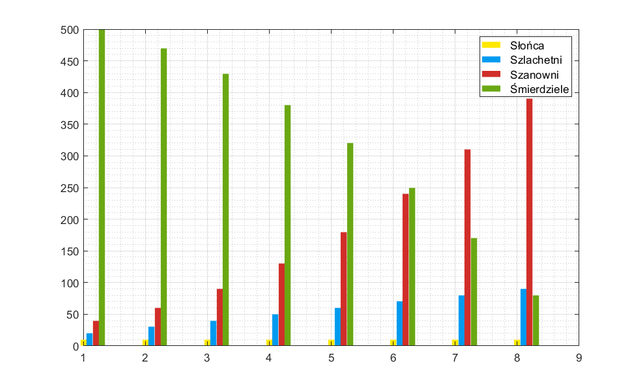
Model – jakkolwiek niedoskonały – mówi nam, że plemię Natchez nie przetrwałoby, funkcjonując w ten sposób, nawet pięciu generacji. Zabrakłoby Śmierdzieli. Koniecznym byłoby wówczas wprowadzenie modyfikacji w system zawierania małżeństw lub… porwanie Śmierdzieli z sąsiednich wiosek. Załóżmy, że w piątym pokoleniu była wojna, na której Natchezi wzbogacili się o jeńców wojennych, których przechrzcili na zwykłych Śmierdzieli – 150 osób (nie uwzględniając małżeństw w tej generacji). Skutkiem wojny były także straty w liczebności arystokratów, odpowiednio: minus 30 Szanownych, oraz kilka awansów: plus 30 Szlachetnych.
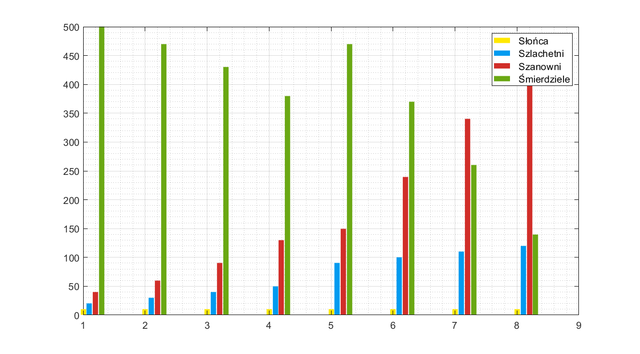
Wykres nam mówi, że wojna niewiele dała. Możliwe, że poszerzyły się tereny Natchezów, jednakże klasa Śmierdzieli wyczerpuje się znów bardzo szybko. Spróbujmy teraz dwukrotnie zwiększyć populację początkową Śmierdzieli – wariant bez wojny.
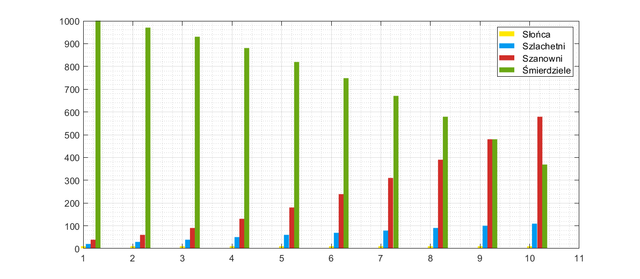
I wariant z wojną:
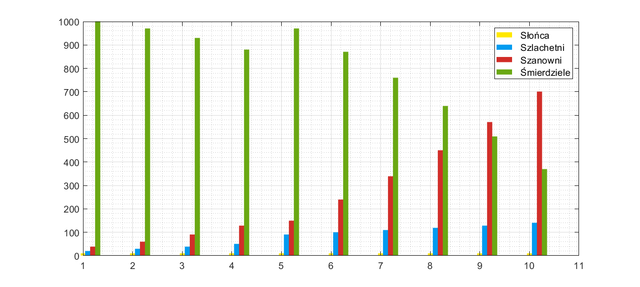
Znów mało efektywna zmiana. A gdyby tak pociągnąć symulacje dalej i zobaczyć 30, 50, 100 generacji? Kolejne słupki ukażą nam skalę deficytu Śmierdzieli na przestrzeni wieków i być może to będzie kluczem do zachowania stabilności systemu. Poniżej wykres dla 30 generacji.
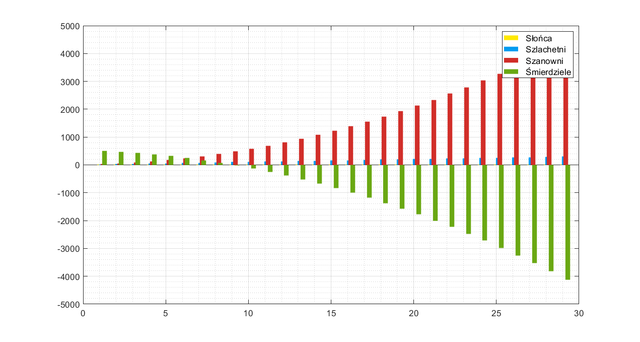
Wykres mówi jednoznacznie: grupa Szanownych powiększa się w zastraszającym tempie, które jest za szybkie na każde działania wojenne. W dodatku minusem jest to, że populacja Słońc nie może się powiększyć na drodze naturalnej, konieczne są awanse ze stopnia Szlachetnych. Plemię Natchezów musiałoby stać się w efekcie ogromnym imperium. Spróbujmy innego podejścia, sprawdźmy ilu Śmierdzieli musiałoby zasilić szeregi Indian Natchez, żeby populacja funkcjonowała w tym systemie:
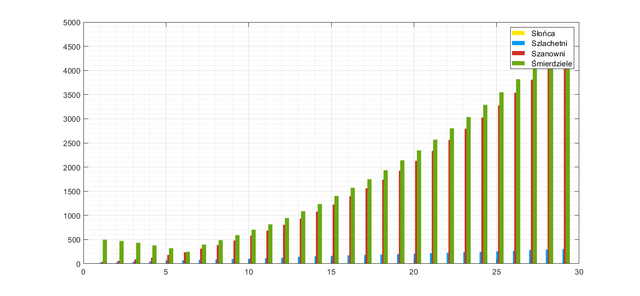
Kod do tego przypadku napisany w Matlabie i wynik w postaci liczby Śmierdzieli w kolejnych generacjach (zakładając, że do 5-tej generacji nie wprowadzono żadnych zmian ze względu na stabilność systemu):
% Indianie Natchez
NOfGeneration = 30;
S = zeros(NOfGeneration,1);
N = zeros(NOfGeneration,1);
H = zeros(NOfGeneration,1);
R = zeros(NOfGeneration,1);
suma = zeros(NOfGeneration,1);
tab = zeros(NOfGeneration,4);
% Populacja wyjściowa
S(1) = 10;
N(1) = 20;
H(1) = 40;
R(1) = 500;
tab(1:4,1) = [S(1) N(1) H(1) R(1)]';
suma(1) = sum(tab(1:4,1));
%% OPTIMUM
figure
for ii=2:NOfGeneration
if R(ii-1)>(S(ii-1) + N(ii-1) + H(ii-1))
S(ii) = S(ii-1);
N(ii) = N(ii-1) + S(ii);
H(ii) = H(ii-1) + N(ii-1);
R(ii) = R(ii-1) - S(ii-1) - N(ii-1);
tab(1:4,ii) = [S(ii) N(ii) H(ii) R(ii)]';
suma(ii) = sum(tab(1:4,ii));
stem(ii-1,tab(1,ii-1),'LineWidth', 7, 'Color', [1 232/255 0], 'Marker','none')
hold on
stem(ii-1+0.1,tab(2,ii-1),'LineWidth', 7, 'Color', [0 155/255 240/255], 'Marker','none')
hold on
stem(ii-1+0.2,tab(3,ii-1),'LineWidth', 7, 'Color', [209/255 46/255 41/255], 'Marker','none')
hold on
stem(ii-1+0.3,tab(4,ii-1),'LineWidth', 7, 'Color', [106/255 168/255 19/255], 'Marker','none')
hold on
else
S(ii) = S(ii-1);
N(ii) = N(ii-1) + S(ii);
H(ii) = H(ii-1) + N(ii-1);
R(ii) = S(ii) + N(ii) + H(ii);
tab(1:4,ii) = [S(ii) N(ii) H(ii) R(ii)]';
suma(ii) = sum(tab(1:4,ii));
stem(ii-1,tab(1,ii-1),'LineWidth', 7, 'Color', [1 232/255 0], 'Marker','none')
hold on
stem(ii-1+0.1,tab(2,ii-1),'LineWidth', 7, 'Color', [0 155/255 240/255], 'Marker','none')
hold on
stem(ii-1+0.2,tab(3,ii-1),'LineWidth', 7, 'Color', [209/255 46/255 41/255], 'Marker','none')
hold on
stem(ii-1+0.3,tab(4,ii-1),'LineWidth', 7, 'Color', [106/255 168/255 19/255], 'Marker','none')
hold on
end
end
lgd = legend({'Słońca','Szlachetni','Szanowni','Śmierdziele'},'FontSize',13);
set(gca,'FontSize', 13)
grid on
grid minor
R =
500
470
430
380
320
250
400
490
590
700
820
950
1090
1240
1400
1570
1750
1940
2140
2350
2570
2800
3040
3290
3550
3820
4100
4390
4690
5000
Podsumowanie
Symulacje były dosyć sztywno nakreślone, ale czy wyjątki zmieniłyby drastycznie prezentowane przebiegi? Myślę, że jest to trochę bardziej skomplikowane. Należy rozważyć jeszcze kilka opcji, zakładając, że plemię Indian Natchez nie trzymało się swoich zasad dot. małżeństw. Modyfikacje, które mogłyby mieć znaczący wpływ na populację – a raczej superpozycja tych zdarzeń – są następujące: możliwość zawierania kilku małżeństw przez tego samego osobnika, przyjęcie wyższej dzietności w klasie Śmierdzieli, reformy społeczności degradujące niezasłużonych Szanownych (najszybciej rosnąca grupa) do klasy Śmierdzieli, migracje ludności. Złożenie tych przypadków mogłoby mieć wpływ na utrzymanie zdrowej proporcji pomiędzy arystokracją, a proletariatem. Innym rozwiązaniem mogłoby być wprowadzenie klasy średniej oraz modyfikacja systemu zawierania małżeństw lub jego całkowite zniesienie. Takie rozwiązanie zahamowałoby polaryzację ludności na dwie grupy oraz wprowadziłoby spokój w demografię plemienia. Klasą średnią mogłaby być wtedy najliczniejsza grupa Szanownych, która stanowiłaby nobilitację dla prosperujących Śmierdzieli, a jednocześnie zagrożenie dla leniwych Szlachetnych i Słońc.
Literatura:
[1] Courant R. i inni — Matematyka w świecie współczesnym, PWN, Warszawa 1966.
[2] Gąssowski J., Łoźny L. — Indianie Ameryki Północnej. Przeszłość i teraźniejszość, Pułtusk 2018 (dostępne tutaj).
Zdjęcia:
[1 - Pixabay]
[2 — Strona fb Negative 1/12 memes]
[3 — Unsplash]
Wpis dodany jako luźne nawiązanie do tematu trzeciego 48. edycji Tematów Tygodnia.
I upvoted your post.
Best regards,
@Council
Posted using https://Steeming.com condenser site.