Czym jest bias przesunięcie i po co nam ono? Skąd się wzięło? Dlaczego warto używać? Czy ktoś tu mówił o funkcji liniowej?

źródło grafiki

Ten artykuł będzie nieco krótszy od dwóch pozostałych - będąc jednak z natury optymistą i szukając jasnych stron życia - mogę stwierdzić, że pozwoli to zaoszczędzić oczy do czytania, i palec do scrollowania :-)

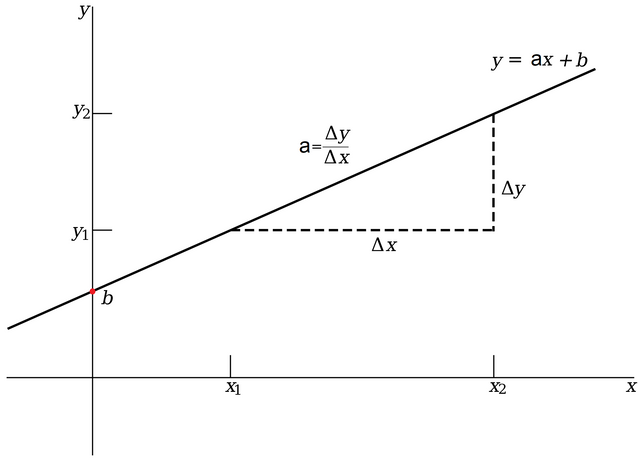
Pewnie wszyscy pamiętamy jedną z pierwszych funkcji matematycznych jakie przyszło nam poznać w trakcie edukacji szkolnej. Mowa oczywiście o funkcji liniowej. Przypomnijmy sobie jak można ją zapisać.

y = ax + b

gdzie:

a - to współczynnik kierunkowy, który decyduje o kącie nachylenia funkcji

b - wyraz wolny określający przecięcie funkcji z osią Y (bias)

x - argument podawany funkcji (wejście funkcji)

y - wartość funkcji (jej wynik, wyjście)

Graficzna reprezentacja funkcji liniowej; źródło grafiki

Jaki to ma związek z klasyfikacją z użyciem neuronów? Spójrzmy jeszcze raz na to co dzieje się w bloku sumacyjnym pojedynczego neuronu:

SUMA_SYGNAŁÓW = Σi = 0 xiwi = Σi = 0 wixi

Zamiana kolejności mnożenia wi z xi nie zmienia wyniku funkcji (bo oczywiście mnożenie jest przemienne), teraz jednak jeszcze łatwiej można zauważyć, że wynik podawany przez blok sumacyjny składa się tak naprawdę ze złożeń funkcji liniowej. Widzimy, że wixi już w samym zapisie wygląda podobnie jak ax, i w gruncie rzeczy jest tym samym - czyli wagę w naszej synapsy traktujemy jako współczynnik liniowy a. Ale chwila, a gdzie nasz wyraz wolny b? No w pewnym sensie on tu jest tylko trzeba go “wyłuskać” (jak fasolę).

If you know what I mean; źródło grafiki

Nasza suma sygnałów sama w sobie jest funkcją liniową, i składa się z innych funkcji liniowych (tzw. złożenie funkcji, np. biorąc dwie garście śniegu i “sklejając” je ze sobą dalej otrzymalibyśmy śnieżkę tylko większą “o innych parametrach”), gdzie wyraz w0x0, możemy potraktować jako b w momencie gdyby wartość x0 na stałe wynosiła 1, a wtedy dowolna wartość w0 określiłaby przesunięcie b. Innymi słowy wyraz w0x0 = w0 * 1 = w0 = b, co aktualizując ogólny przypadek bloku sumacyjnego z #1, możemy zapisać jako:

SUMA_SYGNAŁÓW = b + Σi = 1 xiwi

No dobra, “wyłuskaliśmy” ten współczynnik b, ale co nam z niego? Jak przed chwilą pisaliśmy, pozwala on na ustalenie punktu przecięcia funkcji z osią Y, czyli na właśnie przesunięcie całej funkcji w jedną lub drugą stronę w układzie współrzędnych. Co daje nam możliwość przesuwania funkcji w kontekście sieci neuronowych? Polepsza klasyfikację, a raczej należałoby powiedzieć że może polepszyć klasyfikację. W dalszych częściach będziemy zakładać, że wyraz wolny b istnieje i może przyjąć pewną wartość, która przesunie naszą funkcję sumy sygnałów w układzie współrzędnych, albo liczbą 0 - czyli wtedy wyłączymy jakiekolwiek przesunięcie.

Graficzna reprezentacja działania bias'u; źródło grafiki: Mistrz Paint'a, czyli ja :-)

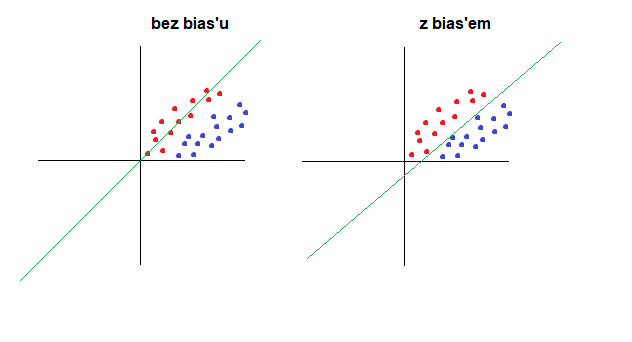
Bias przesunięcie jest również czasem nazywany “obcięciem” (samo "bias" oznacza "ścięcie ukośne"), bo faktycznie w pewnym luźnym kontekście rozumienia, przesunięcie funkcji sumy sygnałów sprawia że część danych o podobnej  wartości do danych “prawdziwych” (ale takich danych których w gruncie rzeczy nie chcielibyśmy klasyfikować jako “prawda”), czyli te najbliżej “granicy” klasyfikacji - zostaną obcięte - będąc od teraz klasyfikowane jako “fałsz”. Gdybyśmy nie dodali bias’u, sprawa granicznych wartości dla neuronu mogłaby być niejednoznaczna. Dlatego chcemy je odsunąć i oglądać tam gdzie powinno być ich miejsce - czyli za kratami :-) Myślę, że w najbliższym czasie pokażę to na mobilnym przykładzie, który każdy będzie mógł odpalić bezpośrednio w swojej przeglądarce i przetestować.

Niektóre dane graniczne umieścimy za kratami; źródło grafiki

Dziękuję za uwagę!

Grafika

Potwierdzam że użyłem Zaawansowanego szukania grafik Google z zaznaczoną opcją prawa użytkowania treści: "Do swobodnego użytku, udostępniania lub modyfikowania, również komercyjnego"

Bibliografia

1. R. Tadeusiewicz "Sieci neuronowe" Akademicka Oficyna Wydaw. RM, Warszawa 1993. Seria: Problemy Współczesnej Nauki i Techniki. Informatyka.