Commutations of Observables and Time Dependence of Expectation Values
Disclaimer: I lay no claim to the originality of the basic ideas expounded here. Its distinctness lies more in its scope and in the detail of its exposition.

"Let's do some real science"
Expectation Values of Observables
In quantum mechanical sense, what does the expectation value of an observable A mean?
The expectation value of an observable A in a particle state described by a wave function 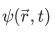 is defined as the average result of N, as it approaches a large number, of measurements of A performed on a particle in the same state
is defined as the average result of N, as it approaches a large number, of measurements of A performed on a particle in the same state 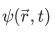 .
.
The prescription for calculating the expectation value of a normalized wave function 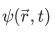 is known as
is known as
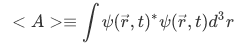
To show that this prescription is the same to the definition of the expectation value as an average, consider the following wavefunction,
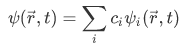
which we have covered on the case on which  is not an eigenfunction of the operator. We substitute this equation to the prescription of the expectation value,
is not an eigenfunction of the operator. We substitute this equation to the prescription of the expectation value,
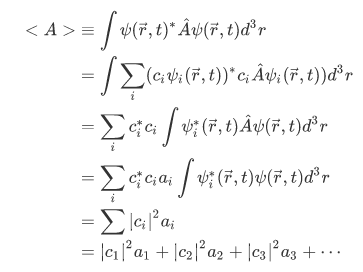
This relation asserts that the expectation value of A in the state  is the sum of all possible outcome
is the sum of all possible outcome 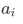 , each weighted by the probability
, each weighted by the probability 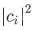 that in this state a measurement of A will yield the result
that in this state a measurement of A will yield the result 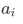 .
.
Commuting observables and simultaneous observability
If the operators corresponding to two observables A and B have a common, complete set of eigenfunctions 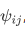 , where we have the i to label the corresponding eigenvalues
, where we have the i to label the corresponding eigenvalues 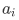 of
of 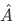 and j labels the corresponding eigenvalues
and j labels the corresponding eigenvalues 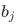 of
of  , we say that A and B can be simultaneously well defined. Another way of saying this is that they have a simultaneously observable.
, we say that A and B can be simultaneously well defined. Another way of saying this is that they have a simultaneously observable.
How do we know that two operators are simultaneously observable?
The commutator 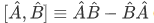 of any pair of simultaneously well-defined observables A and B turns out to be zero. This is a sufficient condition.
of any pair of simultaneously well-defined observables A and B turns out to be zero. This is a sufficient condition.
In some sense, the commutator action on an arbitrary normalizable function 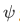 gives zero. Lets show this.
gives zero. Lets show this.
We will use that fact that any such function 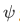 can be written as a linear combination of the common eigenfunctions
can be written as a linear combination of the common eigenfunctions 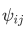 of
of  , so that
, so that
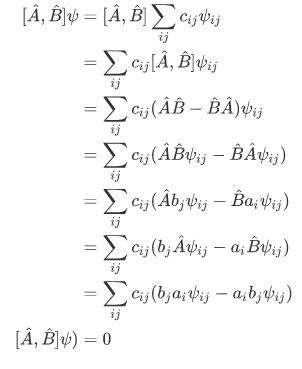
The converse is also true, such that if 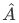 and
and 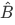 commute, that is,
commute, that is, 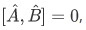 they are simultaneous eigenfunction.
they are simultaneous eigenfunction.
Non-commuting observables and the uncertainty principle
If the commutator  then the observables A and B cannot be simultaneously well defined.
then the observables A and B cannot be simultaneously well defined.
The uncertainty in the observable A in the state 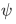 is define by
is define by
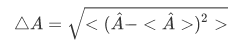
We can show that the product of the uncertainties in two observables A and B is given by the inequality (general uncertainty relation)
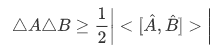
Proof:
Take note of this relation that we derive from previous section,
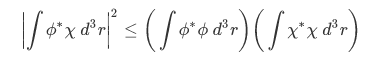
With this in mind, we set 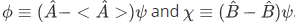 . So we have,
. So we have,
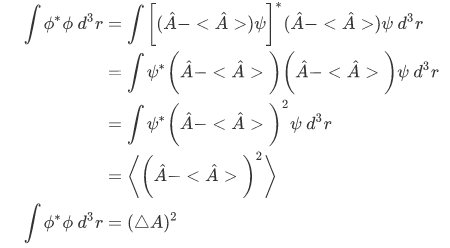
Using a similar line of reasoning we can show that,
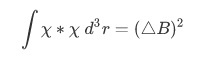
Then the inequality becomes:
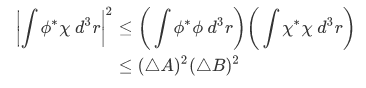
Now what is left is to show what
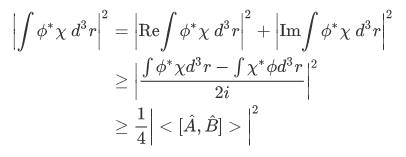
And so we have the following relation,
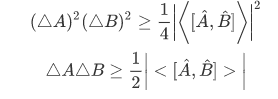
Example: Derive the uncertainty relation of the following operator: 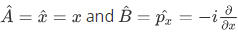 , then we have,
, then we have,
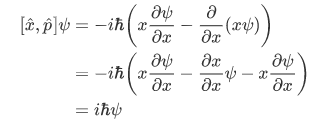
From this we can see that,
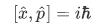
and so the uncertainty relation yields,
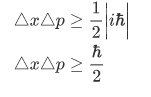
This implies that there is no 1D state 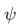 that exists for which the product of the uncertainties of the position and momentum observable is smaller than
that exists for which the product of the uncertainties of the position and momentum observable is smaller than 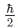 . It is found that in a one dimensional harmonic oscillator in its ground state,
. It is found that in a one dimensional harmonic oscillator in its ground state, 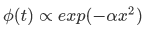 , the uncertainty becomes an equality,
, the uncertainty becomes an equality,
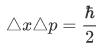
Time dependence of Expectation Values
Use the following expression for the expectation value of an observable A ,
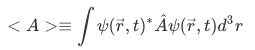
And also the time-dependent Schrodinger equation in the form,
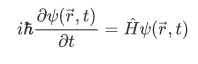
From these equations, we can obtain an expression for the rate of change of the expectation value with time:
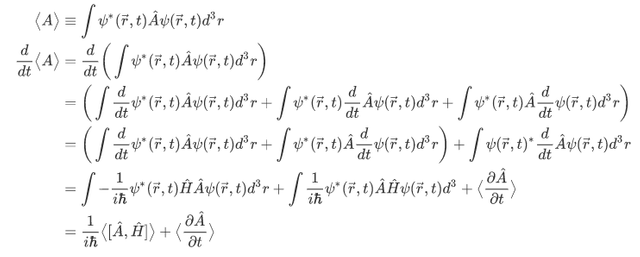
From this we can derive the following expression,
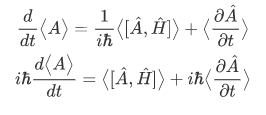
which is known as the Ehrenfest's theorem.
In the fight of Humans vs Bots, @megabot defended you with 20.00% upvote courtesy of @pauldirac!
Support @Megabot by delegating SP to the bot and get a part of 98% of @Megabot's profit.
Direct delegation links : 10 SP || 50 SP || 100 SP || 500 SP || 1000 SP || Any other amount of SP
Join our discord group here.
Thank You !