2/200 Paradojas Resueltas "El cuadrado perdido"
El problema del cuadrado perdido es una paradoja muy conocida y utilizada en el inicio del estudio de la geometría, dentro del campo de las matemáticas.
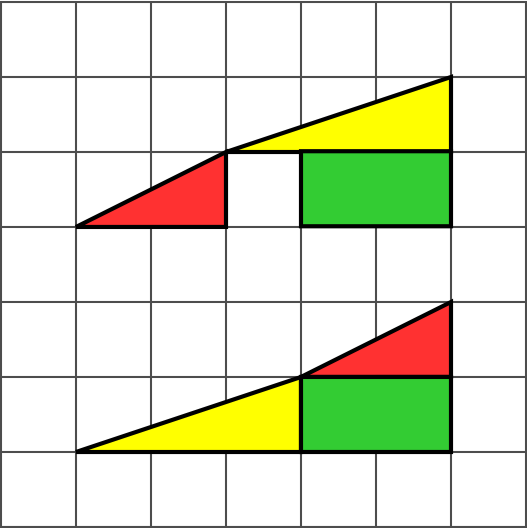
La paradoja consiste en la reordenación de los elementos del triángulo de la imagen superior. ¿Cómo es posible que sólo reordenando las mismas piezas, nos sobre ese espacio cuadrado?
La clave de la paradoja está en el hecho de que ninguno de los triángulos tiene el mismo área que sus piezas componentes. El área de cada pieza es:
Pieza roja: 12 cuadrados.
Pieza verde: 8 cuadrados.
Pieza amarilla: 7 cuadrados.
Pieza azul: 5 cuadrados.
Las cuatro figuras (amarilla, roja, azul y verde) ocupan un total de 32 cuadrados, pero el triángulo tiene 13 de base por 5 de altura, lo que supone un área de 32,5 cuadrados.
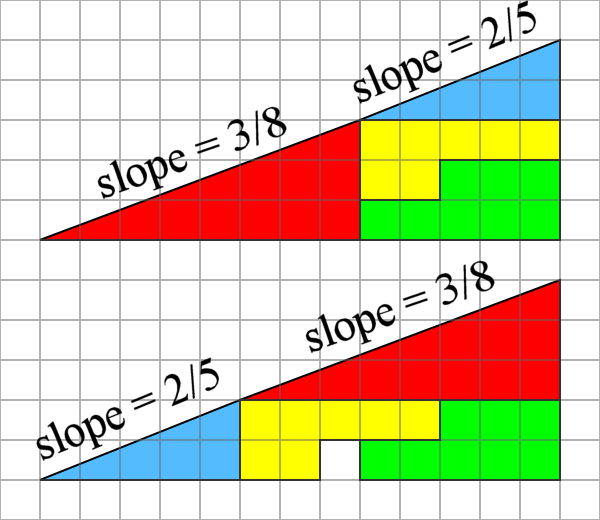
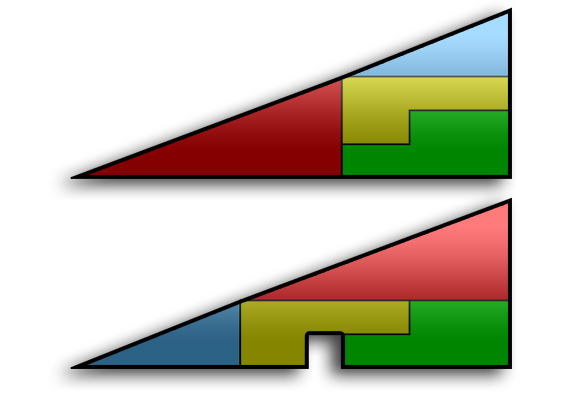
La paradoja tiene una explicación simple: la figura presentada como un triángulo no lo es en realidad, debido a que en realidad tiene cuatro lados, y no los tres propios del triángulo. La "hipotenusa" no está formada por una recta, sino por dos con pendientes ligeramente distintas. Si comparamos los ángulos de inclinación de la hipotenusa respecto de la base de los triángulos rojo y azul vemos que son distintos. En el triángulo rojo el ángulo es 20.55°, mientras que en el azul es 21.8°. Así, la suma de los tres ángulos en la figura de arriba es menor que 180°, mientras que en la figura de abajo la suma de los tres ángulos es mayor que 180°.