Fast Music Theory: Intervals

soundreasoning (53)in #music • 8 years ago

This is the fourth chapter of the pre-release of my book Fast Music Theory: Understanding the Language of Music in Record Time. To start from the beginning, check out Chapter One: 12 Tones. For the previous chapter, check out Chapter Three: Melody and Harmony. Follow me through to the end to grasp more deeply the patterns and tendencies of human sound.

CHAPTER FOUR

Intervals

“A lot of music is mathematics. It’s balance.”

-Mel Brooks

Each note is a landmark. When moving from note to note, we are traveling musical distances. Knowing the names of these distances, or intervals, allows us to see patterns, build structures, and communicate with other music makers.

Half Steps and Whole Steps

We have 12 basic intervals that go along with our 12 tones, but first we need a counting system.

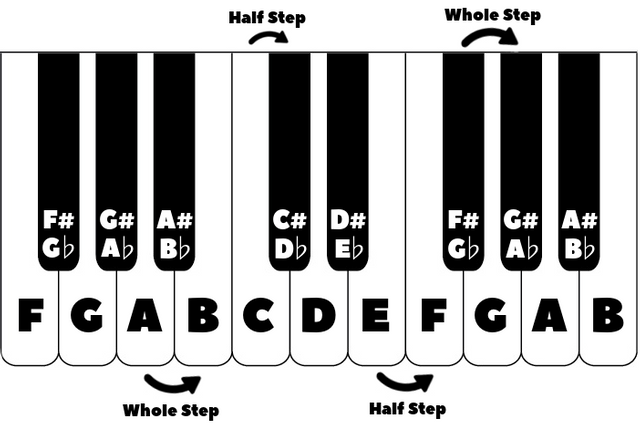
Traveling from C to C# is a half step, which is the smallest distance you can travel in music. E to F is also a half step, so half steps are not determined by “white to black” or any such shortcut. A to B is a whole step, which is two half steps. F# to G# is a whole step as well because the two of them are separated by a G. Half steps are not necessarily intervals, but musical units of measure, like inches. In this guide, we’ll be counting everything in half steps.

Now we can name different intervals. Each new half step results in a new interval. I’ve named the keys in the image based on their relation to the note A.

1 half step = minor 2nd (m2)
2 half steps = Major 2nd (M2)
3 half steps = minor 3rd (m3)
4 half steps = Major 3rd (M3)
5 half steps = Perfect 4th (P4)
6 half steps = Tritone (TT)
7 half steps = Perfect 5th (P5)
8 half steps = minor 6th (m6)
9 half steps = Major 6th (M6)
10 half steps = minor 7th (m7)
11 half steps = Major 7th (M7)
12 half steps = Perfect octave (P8)

FUN FACT: Moving three whole steps in either direction gives you the aptly named tritone (sometimes called the diminished 5th). Because of it’s dissonance and it’s measurement of 6 half steps, the tritone was labelled “the devil’s interval” and avoided in classical tonality.

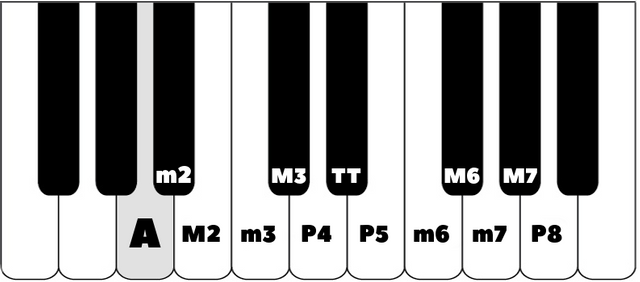
See any patterns? Some of our intervals have minor/major variations to demonstrate their “size.” Some intervals are perfect, meaning they harmonize more consonantly. The tritone is the mid-point between octaves (with A on bottom and A on top) and it is very dissonant. Do you see how the intervals fan out from the tritone? It’s surrounded by perfect intervals, and then minor/major intervals. Or, if you were to read the intervals from left to right, you’d have something that’s almost palindromic (the same forward and backwards).

Consonance and Dissonance

We can think of 6 of these intervals as belonging in groups that have similar properties. Consonance is how well two or more notes harmonize with each other based on the mathematical relationship between their frequencies. Notes that don’t harmonize well are considered dissonant. We experience these as “cleanliness” of sound, or lack thereof. Consonant notes exist together so well that repeating them for long enough almost makes them sound like one note. Dissonant notes produce a wobbly and almost violent tone when played together. Here are some intervalic properties.

Perfect octaves** are so consonant that humans eventually gave notes at this distance the same names as each other.
Perfect 4ths and 5ths** are very consonant, but when harmonizing a moving melody, they tend to sound blocky and less colorful.
3rds and 6ths are slightly less consonant, but harmonize well while moving.
2nds and 7ths are dissonant and make for messy harmonizations.
Tritones are highly dissonant and are forbidden in traditional harmony. Don’t let that stop you from experimenting, though!

Inversions

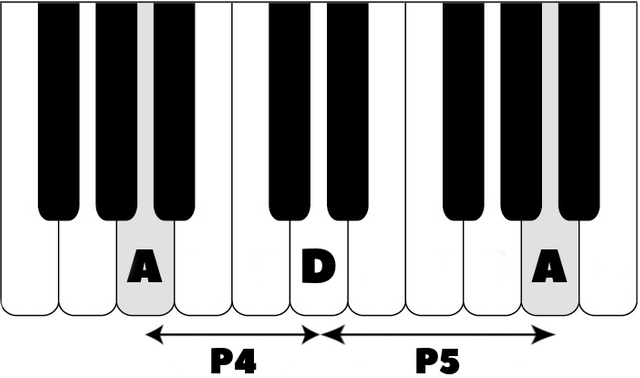
Some intervals are related because they are the same when inverted. For example, a perfect 4th from A to D becomes a perfect 5th if I trade the A out for an A an octave higher. Now I have D to A.

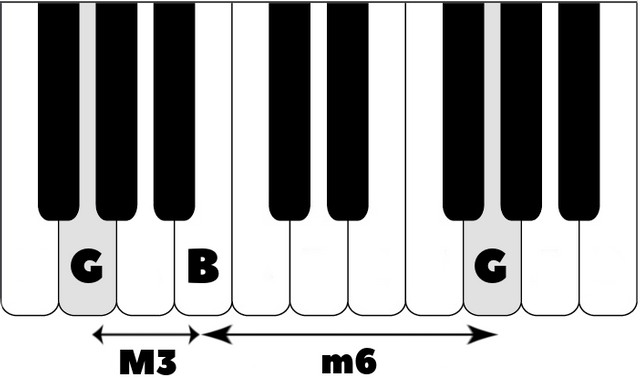
In the next example, a major 3rd of G to B becomes a minor 6th when inverted.

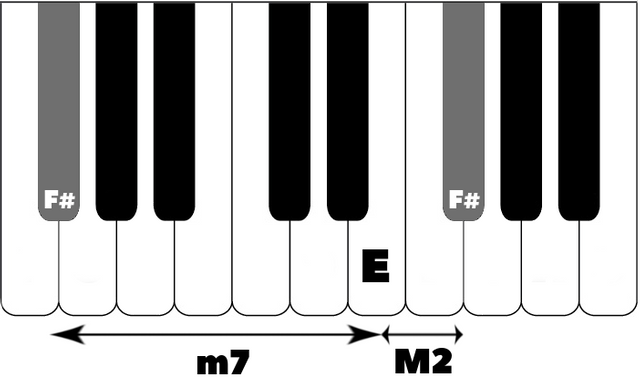
In the next example, a minor 7th of F# to E becomes a major 2nd when inverted.

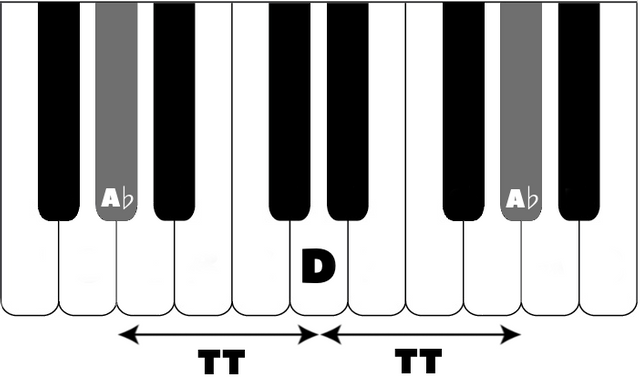
In this final example, a tritone of A♭ to D becomes another tritone when inverted.

These musical distances and their properties make up the melody and harmony of almost every song you’ve ever loved. Learning how to recognize and talk about intervals makes the elusive qualities of music and sound suddenly measurable. You may even find that you gravitate naturally to certain intervals without realizing.

CREATIVITY TIP: Consonance and dissonance are open to interpretation in modern music. Play some of these notes at the same time, determine the interval, and listen to how it sounds! Your own ears will tell you what you like and dislike.

LOOK OUT: There are intervals that are bigger than an octave. They are talked about sometimes, but are generally just used to describe very big chords. We won’t be needing them for this book.

These patterns make up the bulk of musical flavors, no matter what part of the world you're from. Just like the complexity that comes from simple binary, these intervals can be assembled into extremely complex forms and structures. Beginning to think of music as a type of architecture is key to diving deeper into it's powerful affects. Remember, you don't need to be a musician to appreciate these lessons.

Have a music theory question? You can always drop one here.

Was this easy to understand? If not, let me know so I can make the language clearer. Follow me for a breakdown of what it means to "be in key" -- Chapter Five: The Circle of Fifths. Thanks for reading, Steemit community!