Mathematical Explanation - Binary System
Hello friends starting a series of publications related to the science of mathematics today I want to make my first publication talking about binary systems, this post defines its concept, its application and also some examples of binary systems, I invite you to observe this interesting post!
Welcome to the interesting world of mathematics .....
BINARY SYSTEM
The binary system, also called dyadic system1 in computer science, is a numbering system in which numbers are represented using only two numbers: zero and one (0 and 1). It is one of the systems that are used in computers, because they work internally with two voltage levels, so their natural numbering system is the binary system.
History of the binary system

The ancient Indian mathematician Pingala presented the first known description of a binary numbering system in the third century BC, which coincided with his discovery of the concept of number zero.
A complete series of 8 trigrams and 64 hexagrams (analogous to 3 bits) and 6-bit binary numbers were known in ancient China in the classic I Ching text. Similar series of binary combinations have also been used in traditional African divination systems, such as the Ifá, as well as in Western medieval geomancy.
An ordered binary arrangement of the hexagrams of the I Ching, representing the decimal sequence from 0 to 63, and a method to generate it was developed by the Chinese scholar and philosopher Shao Yong in the eleventh century.
In 1605 Francis Bacon spoke of a system by which the letters of the alphabet could be reduced to sequences of binary digits, which could be coded as barely visible variations in the source of any arbitrary text.
In 1670 Juan Caramuel publishes his book Mathesis Biceps; A description of the binary system is given on pages XLV through XLVIII.
The modern binary system was documented in its entirety by Leibniz, in the seventeenth century, in his article "Explication de l'Arithmétique Binaire". It mentions the binary symbols used by Chinese mathematicians. Leibniz used the 0 and the 1, as did the current binary numbering system.
In 1854, the British mathematician George Boole published an article that marked a before and after, detailing a logic system that would end up being called Boole's Algebra. This system would play a fundamental role in the development of the current binary system, particularly in the development of electronic circuits.
Applications
In 1937, Claude Shannon completed his doctoral thesis at MIT, in which he implemented Boolean Algebra and binary arithmetic using relays and switches for the first time in history. Entitled A Symbolic Analysis of Switching Circuits and Relays, Shannon's thesis basically founded the practical design of digital circuits.
In November of 1937, George Stibitz, working at Bell Laboratories at the time, built a relay-based computer - which he nicknamed "Model K" (because he built it in a kitchen, in English "kitchen") - which used the binary sum to perform the calculations. The Bell Laboratories authorized a complete research program at the end of 1938, with Stibitz in command.
On January 8, 1940 they completed the design of a "Complex Number Calculator", which was able to perform calculations with complex numbers. In a demonstration at the conference of the American Mathematical Society, on September 11, 1940, Stibitz managed to send commands remotely to the Complex Numbers Calculator through the telephone line through a teletype. It was the first computer machine used remotely through the telephone line. Some participants of the conference that witnessed the demonstration were John von Neumann, John Mauchly and Norbert Wiener, who wrote about this event in his different types of memories in which he achieved different achievements.
Representation
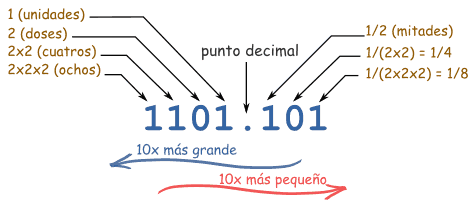
In the binary system only two numbers are needed.
In computing, a binary number can be represented by any sequence of bits (binary digits), which usually represent any mechanism capable of using two mutually exclusive states. The following symbol sequences could be interpreted as the same binary numerical value:
1 0 1 0 0 1 1 0 1 1
¦ − ¦ − − ¦ ¦ − ¦ ¦
x o x o o x x o x x
y n y n n y y n y y
The numerical value represented in each case depends on the value assigned to each symbol. In a computer, numeric values can represent two different voltages; they can also indicate magnetic polarities on a magnetic disk. A "positive", "yes", or "about the state" is not necessarily equivalent to the numerical value of one; this depends on the nomenclature used.
According to the most common representation, which is using Arabic numerals, binary numbers are commonly written using symbols 0 and 1. Binary numbers are often written with subscripts, prefixes or suffixes to indicate their base. The following notations are equivalent:
- 100101 binary (explicit declaration of format)
- 100101b (a suffix indicating binary format)
- 100101B (a suffix indicating binary format)
- bin 100101 (a prefix indicating binary format)
- 1001012 (a subscript that indicates base 2 (binary) notation)
-% 100101 (a prefix indicating binary format) - 0b100101 (a prefix indicating binary format, common in programming languages)
Example 1
Transform the decimal number 131 into binary. The method is very simple:
131 divided by 2 gives 65 and the remainder equals 1
65 divided by 2 gives 32 and the remainder equals 1
32 divided by 2 gives 16 and the remainder equals 0
16 divided by 2 gives 8 and the remainder equals 0
8 divided by 2 gives 4 and the remainder equals 0
4 divided by 2 gives 2 and the remainder equals 0
2 divided by 2 gives 1 and the remainder equals 0
1 divided by 2 gives 0 and the remainder equals 1
-> We sort the waste, from last to first: 10000011
In binary system, 131 is written 10000011
Example 2
Transform the decimal number 100 into binary.
Another form of conversion consists of a method similar to prime factorization. It is relatively easy to divide any number by 2. This method also consists of successive divisions. Depending on whether the number is even or odd, we will place a zero or one in the column on the right. If it is odd, we will subtract one and continue dividing by two, until we reach 1. Then we can only take the last result of the left column and all of the ones in the right column and sort the digits from bottom to top.
Example 3
100 | 0
50 | 0
25 | 1 -> 1, 25-1 = 24 and we continue dividing by 2
12 | 0
6 | 0
3 | 1
1 | 1 ->
(100) _ {10} = (1100100) 2}
(100) 10 = (1100100) 2
Example 4
To convert to the binary system the decimal number 77 we will make a series of divisions that will yield the following results:
77/2 = 38 Residue ==> 1
38/2 = 19 Residue ==> 0
19/2 = 9 Residue ==> 1
9/2 = 4 Residue ==> 1
4/2 = 2 Residue ==> 0
2/2 = 1 Residue ==> 0
1/2 = 0 Residue ==> 1
Now taking the Waste in reverse order the result is:
In reverse order: 1001101 (binary)
There is a last method called distribution. It consists of distributing the necessary ones between the successive powers of 2 so that their sum turns out to be the decimal number to convert. For example, number 151, for which the first 8 powers of 2 will be needed, since the next one, 28 = 256, is greater than the number to be converted. Start by putting a 1 in 128, so there will still be 23, 151-128 = 23, to get to 151. This value will be achieved by distributing some among the powers whose sum gives the desired result and putting zeros in the rest. In the example, they are the powers 4, 2, 1 and 0, that is, 16, 4, 2 and 1, respectively.
Example 5
20 = 1 | 1
21 = 2 | 1
22 = 4 | 1
23 = 8 | 0
24 = 16 | 1
25 = 32 | 0
26 = 64 | 0
27 = 128 | 1
128 + 16 + 4 + 2 + 1 = (151) 10 = (10010111) 2}
128 + 16 + 4 + 2 + 1 = (151) 10 = (10010111) 2
References :
- Thomas: Infinitesimal calculus and analytical geometry, Aguilar, Madrid. See also Drae
- BCD, hexadecimal, etc; "Digital mathematics"
- ING. EVA VIVEROS ZENTENO. "Discrete mathematics". Consulted on March 14, 2106.
- Nieves, Antonio (1999). Numerical methods. Continental, S.A de C.V.