Knowing The Math - What is the Continuous Division Method for finding the HCF (Highest Common Factor)?

In this post we will understand the continuous division method to find the hcf of two numbers say we want to find the hcf of 24 and 36 this method is generally used for large numbers

But first, let's try it out with smaller ones

As the name says we have to use division

In the first step we divide the greater number by the smaller number

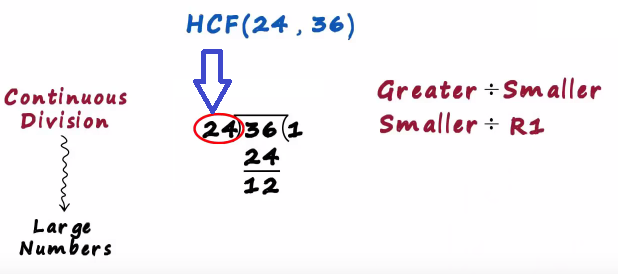
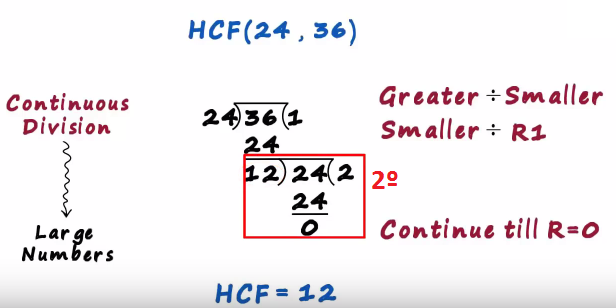
Here 36 is the greater number so we divide 36 by 24 we are generally used to writing the quotient on top

But in this method we will write like in the image

24 x 1 is 24 and 36 minus 24 is 12

But wait, we're not done yet the name says continuous division

This was just the first part we got the quotient as 1 and the first remainder as 12

We call this the first remainder as we get many remainders in this method

In the second step we divide the smaller number by the first remainder

The smaller number is 24

So we write 24 there

We are dividing the smaller number by the first remainder 12 times 2 is 24

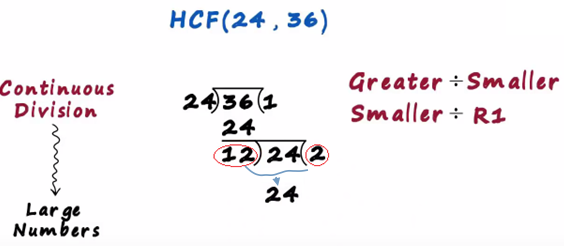
And 24 minus 24 is 0 we continue this till we get the remainder as zero and guess what we already have the hcf

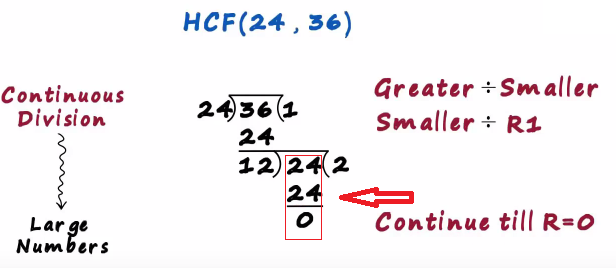
The final divisor becomes the hcf so here the hcf will be 12

the hcf of 24 and 36 is 12

We divide continuously till we get the remainder is 0 this part was a first division

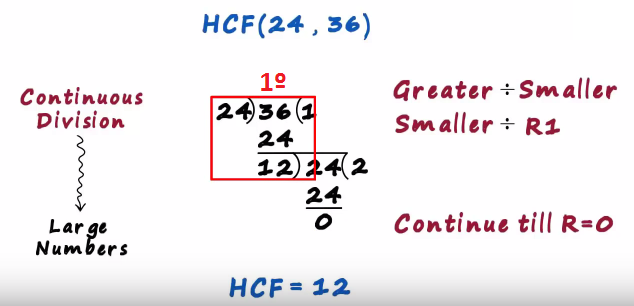
And this was a first remainder

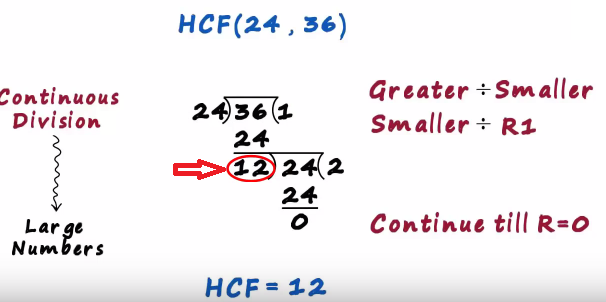
Since it was zero, we perform the second division

In which the smaller number became the dividend

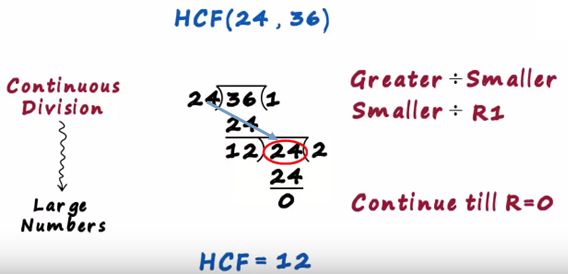
And we continue this Till we got 0

But wait, what if they wouldn't have got a zero here what would be the next dividend let's look at another example to understand that

We try to find the hcf of 1044 and 1512 in the first step we divide the larger number by the smaller number

That is, we divide 1512 by 1044

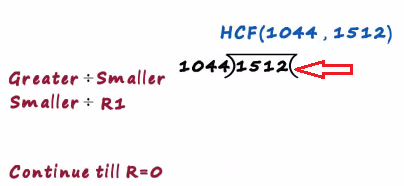
1044 times 1. is 1044 one is the largest Quotient possible here since 1044 times 2 is 2088 which is greater than 1512

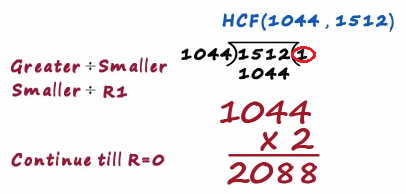
And 1512 minus 1044 is 468 this becomes a first remainder

Since it's not zero, we continue with that division the smaller number becomes the next Dividend

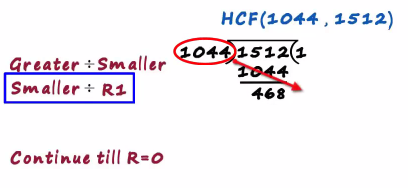
And the first remainder becomes the Divisor

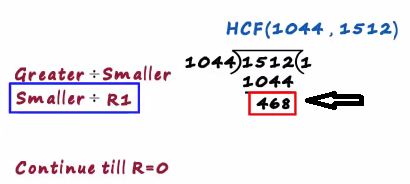
So we write 1044 and then we write 468 times 2 equals 936

And 1044 minus 936 is 108

Now we completed the second stage and the remainder is not 0 so how do we continue further well, it's easy the first remainder becomes the divided

And the second remainder becomes the divisor

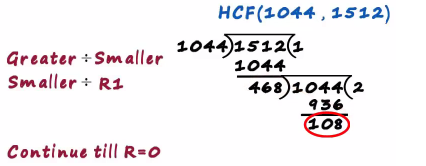
we can write the next step as r1 divided by r2

The first remainder is 468 so we write it this is r1 divided by r2 this is the 3rd division we are performing for this example

468 times 4 equals 432 and 468 minus 432 is equals to 36 the remainder is still not 0

The next step is simple it will be our R2 divided by R3 108 is the second remained and 36 is the third remainder

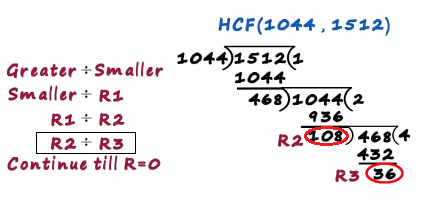
Hence we write the second remainder, which is 108 here

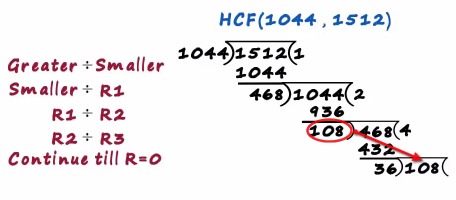
We are dividing R2 by R3

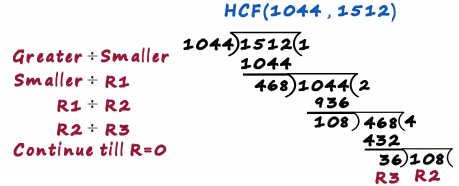
36 times 3 is108 and finally we get the remainder at zero

That's where we stopped and the final divisor becomes the hcf hence the hcf of 1044 and 1512 is 36

There is another way in which you can look at it, look at the first example

If the remainder is not 0 the divisor becomes the next dividend, it's the same thing in the second example where we performed for division processes one two three and four

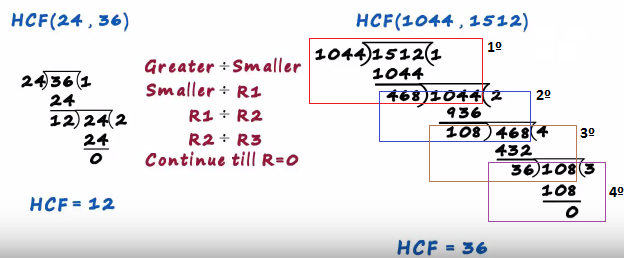
The first remainder was non zero 1044 became the next dividend

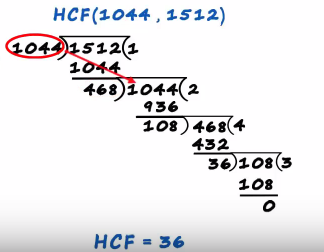
Then 468 became the next devident

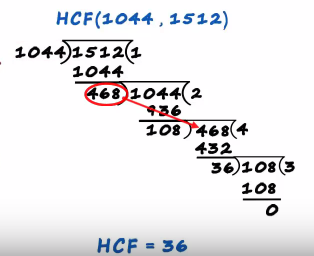
Since was not zero and then 108 it became the next devident

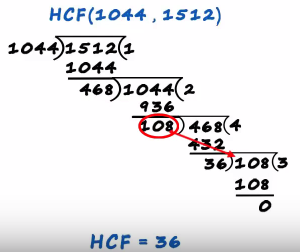
and we stopped since the remainder became 0 and for every division process the remainder is the divisor and remember once you get the remainder at zero the final Divisor becomes the hcf