Knowing The Math - Square roots for algebra

Square roots for algebra 1 we're gonna talk a little bit about what square roots are wen 2 equal factors or a number when multiplied together they result in that original number, for example 4 times 4 is equal to 16

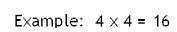
So 4 is a factor of 16 and will multiply by Itself gives us the original number back so we would say 4 is the square root of 16

Here are some numbers that are nice to remember wen we're talking about square roots

The numbers in green are called perfect squares in other words you multiply the same number times itself, you'll get out as a result, so 1 times 1 is 1, 2 times 2 is 4, 3 times 3 is 9 5 times 5 is 25 all the way down these are the numbers that you want to take a look at

And when you see a number that is like, this is a perfect square is a nice number to work with, we are talking about getting square roots

Square roots symbol looks like in the image square root of 36

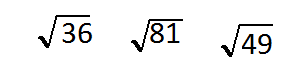
And 6 times 6 is equal to 36 so we can rewrite square root in that form in other words like this

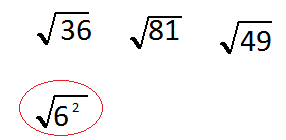
6 squared we was just change 36 to be 6 squared or 6 times 6 and we know that the square root is the opposite function as the squared that 2 up top so we can cancel them out just like you cancel out multiplication being the opposite of division or addition being the opposite as subtraction they cancel each other out the square root and squared cancel each other out and end up with 6

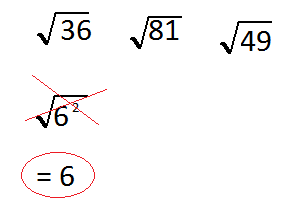
Look at 81 square root of 81. 81 is equal to 9 times 9 or 9 Squared

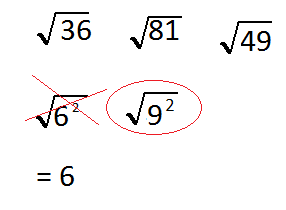
Cancel also both and our result is 9

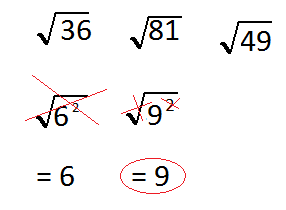
49 is equal to 7 squared

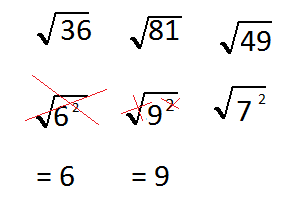
So again we capital out everything and our final result is 7

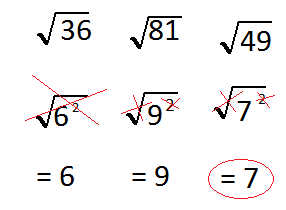
Actually that I do is evaluating Of squares.

Look at some other types of examples and this one We are multiplying together the square root of 18 times the square root of 9

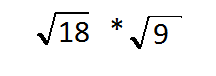
We can write that in another way we could write that as the square root 18 times 9 we can put it all under

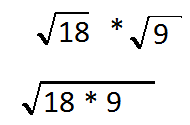
What we saw earlier will show us that we can factory these down now.

We got the square root up of 18 we can make that into the square root of 9 times 2 and then we had the other 9

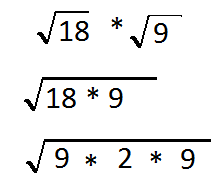
Making kind of like a little bit more work because we couldn't just factored in starting at the beginning, but if you get some numbers that are perfect squares when you're multiplying together it's kind of nice to bring them together and then take them apart again

When we do this we're looking for factors like out look for the factors 18 I, found,something a perfect square 9 because 9 is 3 times 3 and as a perfect square factor of 18 so 18 divided by a perfect square and by doing that i have been able to isolated a coupled perfect squares and then I'll be able to cancel out the perfect square

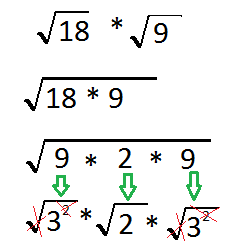
And squared what I get as a result is 3 times Squared 2 times 3 or in other words 9 square root 2

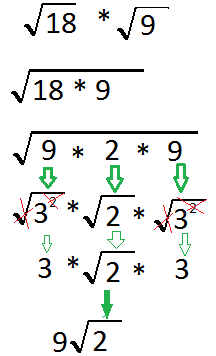
Those are just the steps to solving down here and that's just factoring and the key i think is when you're taking out factors you want to take up factors that are perfect squares hoping to make it more simplified.

Look at another question This is similar to the prior question we're going to take out The factor when I look at these two numbers

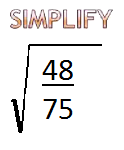
I try and find factors that are perfect squares

So what a factor of 75 it is easy for me because I know 75 is 25 times 3

48 has a lot of different factors, and actually had a lot of perfect square factors so i wanna work With 75 first because it is easier, so I know what that means is 75 can be changed to 25 times 3 alright

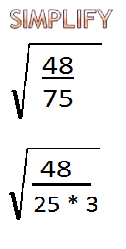
Now 48 also divided by 3 so I'm going to actually take 48 and I'm going to factor it right now 48 his equal to 16 times 3 so ended up working out very nicely because 16 is also a perfect square 16 times 3, in 25 times 3

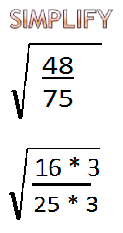
And we can do this in one of two ways we can either say 3 over 3 is 1 so we can cancel it out

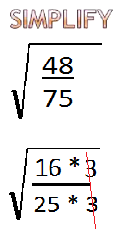
And in other words, we're just reading an equivalent fractions 16 over 25 be equal to 48 over 75

Or if you want to do it another way you can say it is the same 16 over 25 times the square root of 3 over 3

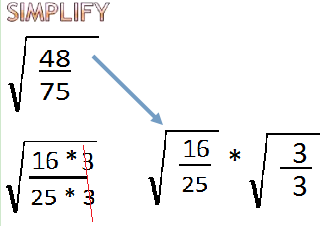
And you can't do that, but essentially what it is doing Is 3 over 3 is 1 the square root of 1 one is 1 so whatever 16 over 25 times 1 and you end up basically canceling that out anyway

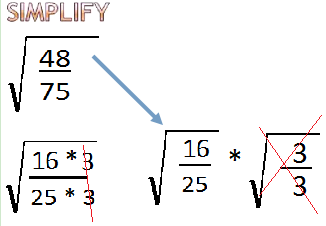
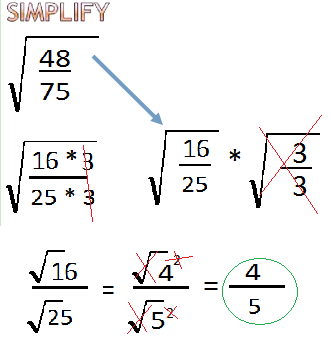
So either way you'll end up with the same result and that is the square root of 16 over the square root of 25 and as we said before 16 and 25 are both perfect squares so it works out really nicely for us as far as finding the solution the square root of 4 squared those 2 will cancel each other out we end up with 4 square root of 5 square Is 5 and that's going to be our final answer right there 4 over 5

In the next type of question is asking us to find the square root of a decimal

A decimal can be written as a fraction and in this case it would be 0.64 is the same of 64 over 100

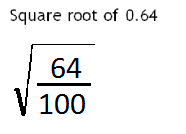
That's the way that we would write this decimal as a fraction just like in the prior question we can now take the square root of 64 and divided by the square root of 100

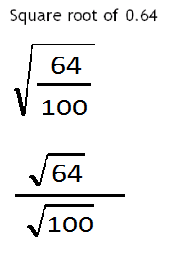
And 64 is equal to 8 squared that's one of those numbers from the beginning

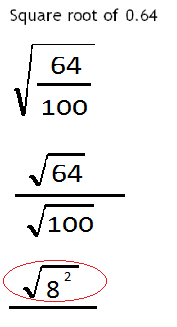
And 100 is equal to 10 squared

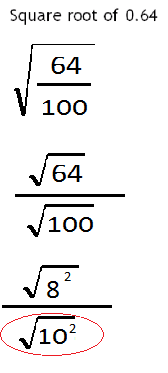
And you see it doing fracturing from these perfect squares goes really quickly because I have memorized that list that I was showing you earlier on knowing your your perfect square factors it's important and that speeds things up.

So capital out square root and squared on each of those and we end up with a 8 over 10 or in other words 4 over 5

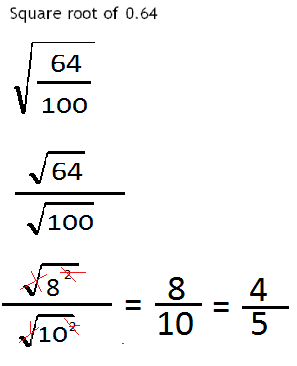
Right, that's going to be our final answer for that question

So if you have a decimal you wanna put it into a fraction form square root out you put it into a fraction form and then factor each top and the bottom Separately alright

For the final question in these mini lesson on square roots, we're gonna look at adding and subtracting square roots

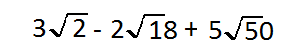
Just like with adding and subtracting Out any other number you want to make sure that you have like terms so we have the square root of 2 from each of these terms in the image and to do that we're going to change the square root of 18 to being the squared of 9 times square root of 2

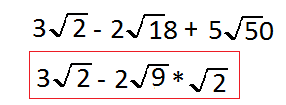
We're gonna to change the square root of 50 to be square root of 25 times square root of 2

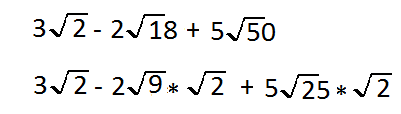
All we're doing is trying to get that factor of 2 out for each term and that way we have a term here we have the square root of 2

We know that's something we can′t factor anymore, that's why we chose that one

Square root of 9 is equal to 3 so that saying 2 times 3 which is 6

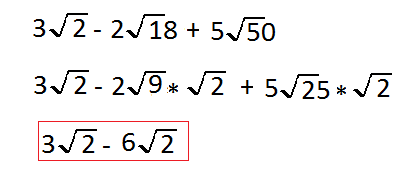
Now we say 5 times the square root of 25 the square root of 25 is equal to 5 The 5 squared is 25 so will say these 5 times that 5 will give us the result of 25 square root of 2

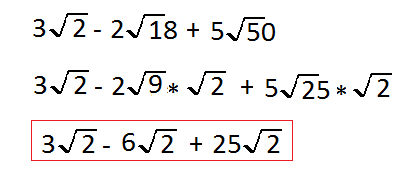
Now that we have the square root of 2 for each term we can now add them all together 3 root 2 minus 6 root 2 is equal to negative 3 root 2 and 25 a positive 25 and will end up with the Result of 22 square root of 2

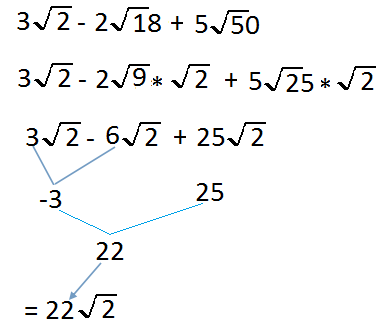
It is the final answer for that question

Hope this has been helpful. Have a wonderful day