Knowing the math - Ratios Part 1
Hello, today we're going to be looking at Ratios the first part of ratios anyway
I first want to explain a little bit about what a ratio is coming the big picture this whole lesson
A ratio is a comparison of two quantities by division. So I'll show you a couple Examples.
The first way we can write it as the fraction like fish over sharks okay, it's a comparison of two quantities like a number fish in a number sharks its related by division see can write it in a fraction form the numerator divided by the Dominator.

You can also write it using a colon fish colon sharks alright this is the second way

And the third way to write a fraction is using words were you would say fish to sharks are at the comparison the fish to the Sharks.

You can write to like the first like the second Or like the third and I'm going to show an Example of each up these matters and actually Solve of three questions using fractions in these three different ways, but just the basic overall idea, it's a comparison in the third case it's a comparison to the number fish to the number of sharks written in three different ways
But look at the fraction former writing ratio when you have a ratio or it might just 13 over 26 you can write it in lowest terms just like you write a fraction in lowest terms the same way that you would write a fraction of all those Terms

Let's go ahead and do that The fraction of 13 over 26 what we'll do is will look for common factors between 13, 26 to do that what I like to do is look at all the factors of 13 and all the factors of 26.
So the factors of 13, 1 and 13 the factors of 26 are 1, 2, 13 and 26

Once we have the factors of 26 and 13 listed want to pick the greatest common factor and in this case that would be 13

And so we will take that number thirteen the greatest common factor and we will divided both the numerator and denominator by 13 this is just reducing down a fraction into lowest terms.

For 16 over 100 the greatest common factor between the Two is 4 again we could list like as above, but is a review of writing fractions in lowest terms and we skip over that up this time and just give you the greatest common factors for.
So we're going to divide each term By 4 and will end up with the fraction of 4 over 25, 16 divided by 4 is 4, 100 divided by 4 is 25 this is our fractional terms or in other words our ratio in lowest terms.
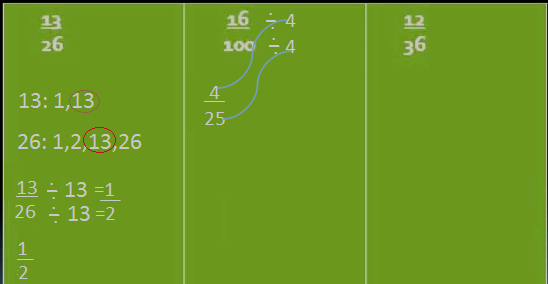
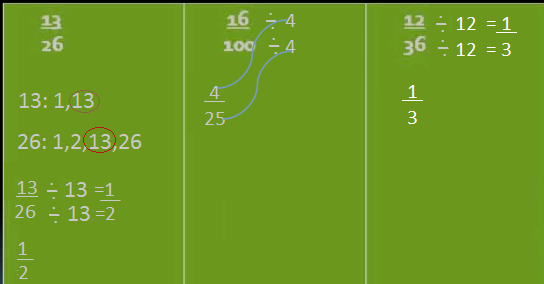
Now we have the fractions 12 and 36 we have to find the greatest common factor there are lot of common factors between these two they have common factors 2, 3, 6 and 12.
12 is the common factor that we're going to be using so we'll divide both the numerator and denominator by 12 we end up with the Result 1 over 3 that is our fraction in lowest terms it's also our ratio in lowest terms
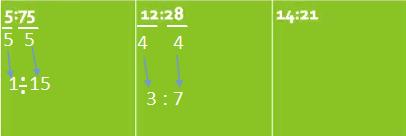
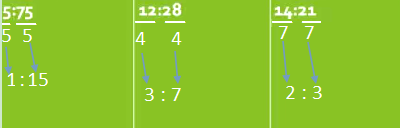
In this next series of ratios were asked to rate these ratios in lowest terms we're going to do exactly the same thing that we did in the previous exercise where we find the greatest common factor and divide each term.

So 5 and 75 are both divisible by five. we could list of the factors if we want we're going to divide each by five we get a ratio of 1 to 15 So 5 divided by 5 is 1. 75 divided by 5 is 15 so we have a ratio of 1 to 15 that is ratio in lowest terms.

Now for 12 and 28, 28 is not divisible by 12 however 28 is divisible by 4 as is 12 so we'll do is we'll divide both terms by 4 such our greatest common factor 12 divided by 4 is 3, 28 divided by 4 is 7 and so with a 3.7 ratio
Final, i have 14 to 21 and 14 and 21 are both divisible by 7 So divided both by 7, 14 divided by 7 is 2 and 21 divided by 7 is 3 so ratio in the lowest terms for this is 2 to 3 that's the way we say a ratio the 2 to 3
So this is essentially the way to do rate ratios in lowest terms exactly the same thing as writing fractions in lowest terms
Let’s go ahead and look at the word way of writing out ratios in this question says Jim had 14 friends
8 were girls 7 were boys write a ratio in lowest terms of the following 3 ratios
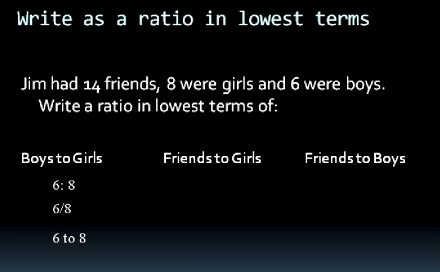
So first ratio in to do is boys to girls so if he had 8 friends who are girls 6 friends who are boys than the boys would be 6 and the girls would be 8 so we can write this again we could write it and several different ways the way I'm going to write it is using 6 to 8 you can write this using the colon as you saw the last one we could righted in the form of a fraction as you did in the first or we can write it into work form
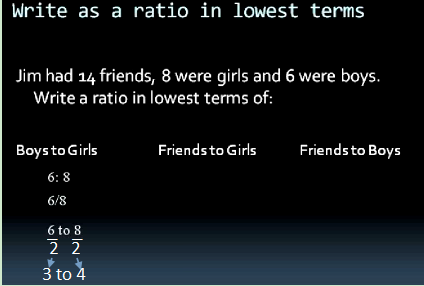
However 6 to 8 is not and its lowest terms so we're going to have to change this into its lowest terms 8 and 6 are both divisible by 2 so if we divide both by 2 will end up with 3 to 4 ratio a boys to girls
Now let's look at the ratio of friends to girls so the total number of friends to the number of girls to about 14 friends . number friends who were girls is 8, so 14 to 8 and we can divide each by 2 to get them into lowest terms as ratio 7 to 4, 7 friends are 4 girls 4, 7 friends are 7 to 4

When we do the ratio of friends to Boys it be 14 that the total number of friends and the number of Boys who were his friends as 6 and we can down the lowest terms by dividing each term by 2, 14 divided by 2 is 7, 6 divided by 2 is 3

So we see that we have three different examples operating ratio and work for and reducing it down to its lowest terms
That is the end up of examples for today's there will be a second lesson about Ratios that's connected with this one.