Knowing The Math - Proportions

Hello everyone, this is our lesson on Proportions again this is breaking broken in 2 parts So this is proportions part 1 for pre-algebra

The main big idea about the proportion is that the proportion is basically to equivalent to ratios alright, or to Equivalent fractions before writing the ratios In fractions here's an example 3 to 4 is equal to 75 to 100 ok here two equivalent ratios so that means that this is a proportion Alright.

We can also write them as two equivalent fractions like I said a second ago, 3 over 4 is equal to 75 over 100 that's the main idea about proportion.

So you've seen this before, it's been called equivalent fractions, it's been called equivalent ratios it's been called reducing to lowest terms an it is now called proportions

There is actually a point to using proportions and I'll show you that in the combination of these lessons, but there is some very practical purposes for looking at proportions Let′s go ahead and take a look at some of Those.

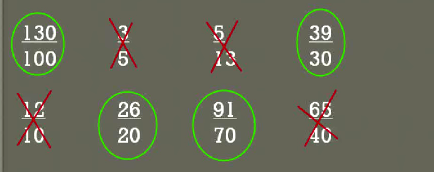
First we are going to do a quick review of equivalent fractions we're going to circle all the ratios that are equivalent to 13 to 10

So something's an equivalent ratio 13 to 10 we can also say it is proportional to 13 to 10

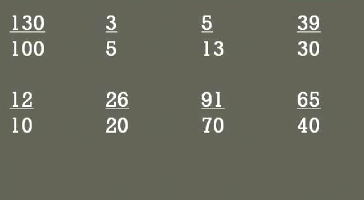
We're going to circle the fractions so look at our first one our first one is 130 over 100 that is 13 times 10 and 10 times, 10 so we know that is an equivalent fraction an equivalent ratio or that is proportional to 13 to 10

How about 3 to 5, 3 to 13, 5 to 10 it's really not we could convert the bottom into 10 by Multiplying times 2 it would be 6 because 3 times 2 is 6 that is the 6 over 10 it's not the same as 13 over 10 so these are not equivalent ratios in other words they're not proportional to each Other.

Look at our next 5 over 13 again, you're not to be able to convert this into an equivalent fraction with 13 over 10 would require a great deal of working together and there's not really a nice number that you multiply 13 times something to get five and 10 times something to get 13 it just doesn't work out.

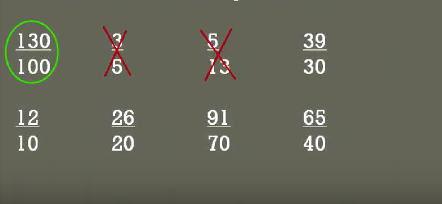
39 over 30 looking at the ratio of 13 to 10 so what would we have to do to is make 10 in to 30 we have to multiply 10 times 3 so 10 times 3 is 30, 13 times, 3 is 39 so now we have 2 fractions that are proportional to the 13 : 10 ratio

Let's go to the next 12 over 10 is 12 to 10 the same as 13 to 10 no it is not

And about 26 to 20 let's do the same thing we did for the 39 to 30 fraction what we have to do the 10 to make it into 20 we multiply it times 2 so 10 times 2 is 20 and how much 13 Times 2 is 26? Yes, it is so therefore we have another equivalent proportion.

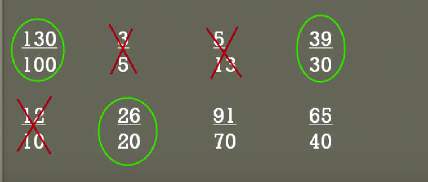
Now we have 91 over 70 let's look at that again, what Times 10 will give us 70, 7 times 10 will give the 70 what 7 times 13 it is 91 so again we have another equivalent fraction or equivalent Ratio

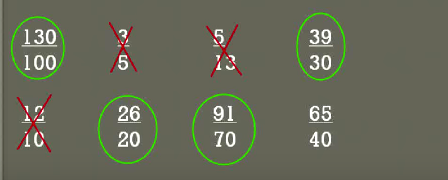
The next we have is 65 over 40 what is 10 times something will give Us 40, 10 times 4 is 40 which 13 times 4, 13 times 4 is equal to 52 Is not 65 so therefore that one Is not equivalent alright so this is just a little exercise.

How do I find out if these are equivalent you could also write 13 : 10 as a fraction 13 over 10 And you trying to see which ones are equivalent fractions, that's essentially what I was doing so this is just a basic to little practice together thinking about equivalent fractions equivalent ratios for another words proportions.

Let's write are own portions were gonna take any two numbers 6 over 23 these are the two that I mean use so to write your own proportion you use any numbers what you're going to do is multiply both the numerator and the denominator by the same number so I'm gonna multiply 6 and 23 times by the same number and we'll see what happens.

So look pick another random number 15 I picked it doesn't matter which number you use as long as you multiply it by both the top and the bottom So 6 times 15 and 23 times 15, look that 6 times 15 is 90 and 23 times 15 is equal to 345 so what we have here is an equivalent fraction okay 6 over 23 is equivalent to 90 over 345 in other words these two fractions are proportional to each other where they are equivalent ratios or equivalent fractions.

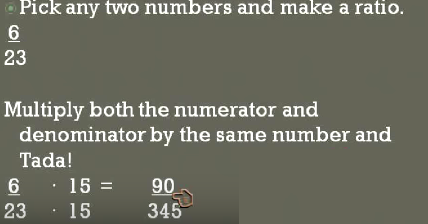
I hope you enjoy ,hope you had a great time and I hope that has helped you understand proportions a little bit Better. Had a wonderful day.