Knowing The Math - Mental Tricks - Multiplication Part 1
How could you multiply 9 with 8 some of you have probably memorize the multiples of 9 and know the answer we know that it is 72
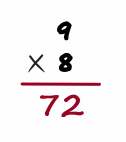
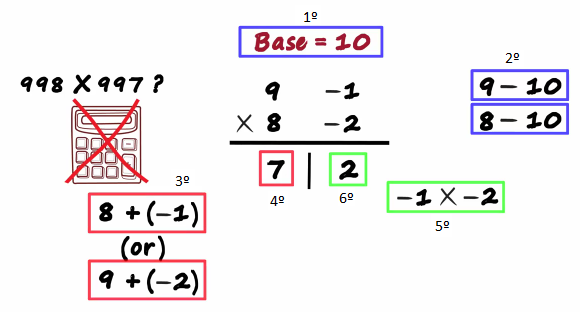
But in this session we will understand multiplication in a very different way will this different way help us? Well, let me put it this way understanding this technique will help us solve problems like 998 times 997 in about five seconds yes without a calculator.

We use the concept of Base to solve multiplication problems quickly and bases that generally powers of 10 like 10, 100, 1000 and so on
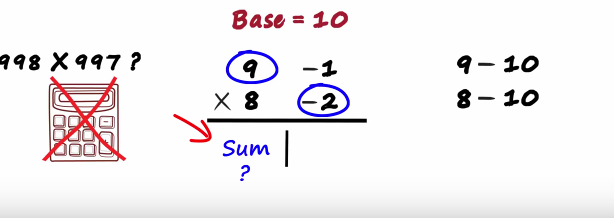
When we are given the multiplication problem the first thing we should ask ourselves this which base is close to both the numbers? here both numbers are close to 10 so we can say that the bases is 10 once the bases decided life becomes really easy first we subtract the base from each of these numbers, subtracting the base from the first number we get 9 minus 10 that equals minus 1 We write it next to that number

Next would be 8 minus 10 that equals minus two
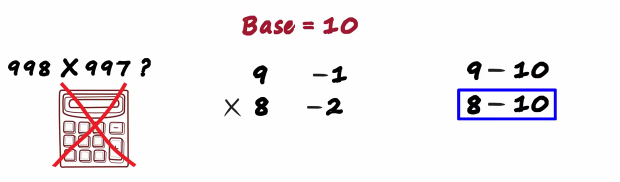
These two numbers tell us how far these two numbers are from the base. 9 is minus 1 units away from the base and eight is minus 2 units away from the base so the initial two steps choose the base and subtracted from the numbers once this is done just make a partition like in the image
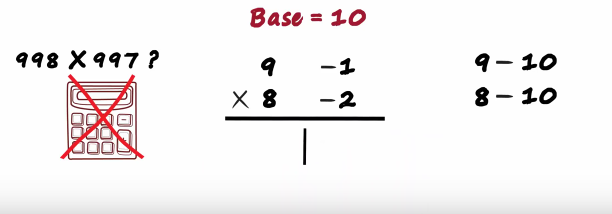
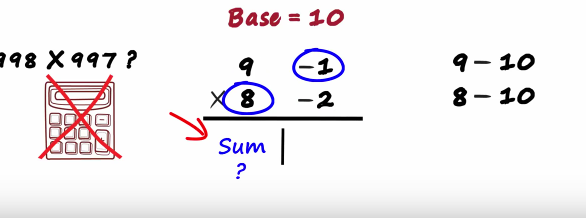
On the Left we write the sum what sum? the sum of the two numbers
Ore the other two numbers
Both will result in the same answer 8 plus minus 1 or nine plus minus 2 both equals to seven

So we write a seven on the left on the right we have the product of these two Numbers
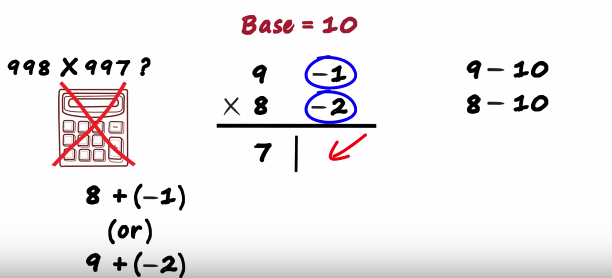
Minus 1 multiplied by minus 2 and that equals to 2 Yes, we should also consider the sign when we multiply these two numbers.
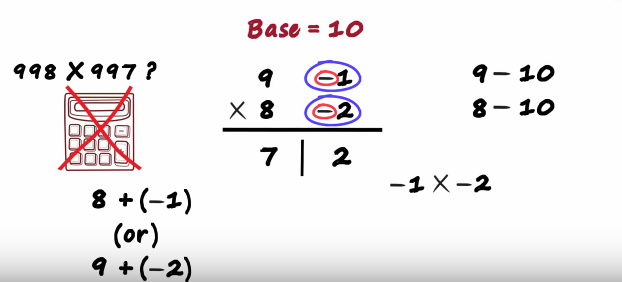
there you go we have the answer 9 times 8 is 72.
The steps are simple, we find the base, then subtracted from each number write the sum on the left and the product on the right.
Is there anything we need to be careful about here? Yes on the right the number of digits should be equal to the number of zeros in the base
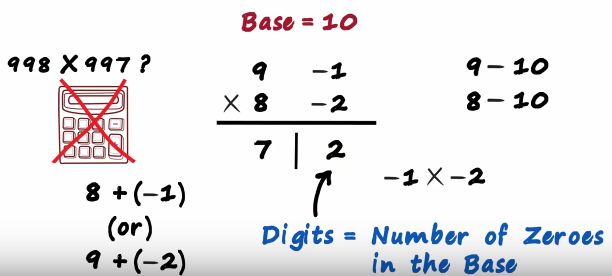
Here the base has one zero so we write just one digit on the right don't worry everybody thinks this is difficult at first
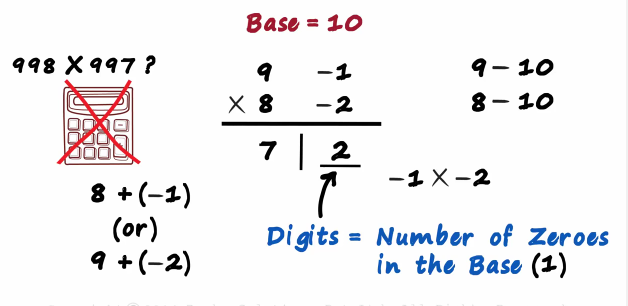
So let's quickly solve a couple of problems and you will see how simple this technique actually is.
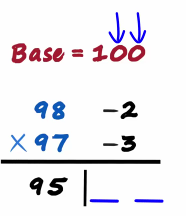
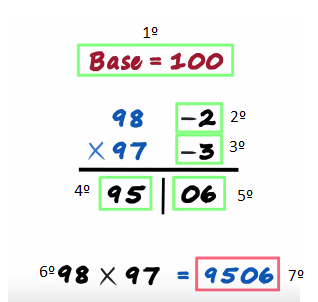
Say we want to multiply 98 with 97 both these numbers as we can see are close to 100 so the bases is 100. 98 minus 100 is minus 2 and 97 minus 100 is minus 3

Then we make a partition on the Left we write the sum and on the right we write the product
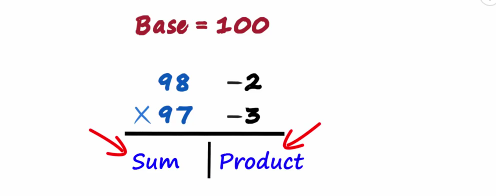
98 plus minus 3 is 95
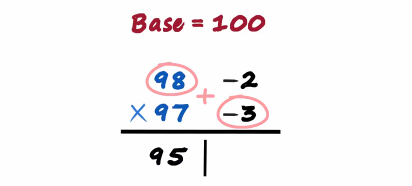
Even 97 plus minus 2 will give us 95
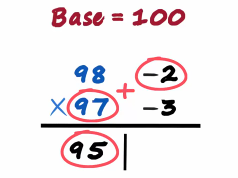
And minus 2 times minus 3 is 6 so should we write a six
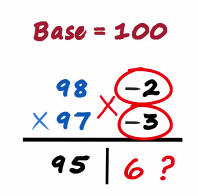
Don't forget the number of digits on the right will be equal to the number of zeros in the base
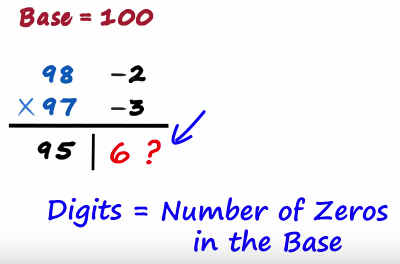
As there are two zeros in 100 there will be two digits there
Six will be 06
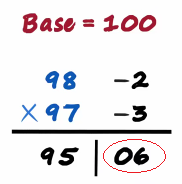
There's your answer 98 times 97 is 9506

Find the base, find the deviation, find the sum and find the product and we get the answer in a few seconds
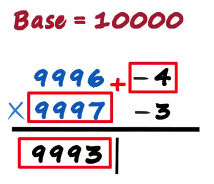
Ok, let's try solving a problem with slightly bigger numbers 9996 times 9997 why don't you try this remember the four simple steps, find the base find the deviation find the sum and find the product.

Both numbers as we can see are close to 10,000 so the base will be 10,000

Number 9996 is minus 4 units away and 9997 is minus 3 units away

Then we make the partition sum on the left and the product on the right

9996 Plus minus 3 is 9993
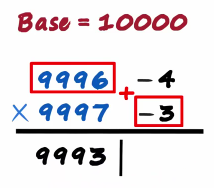
The sum of 9997 plus minus 4 will also give us 9993
The product will be minus 4 times minus 3 which equals 12
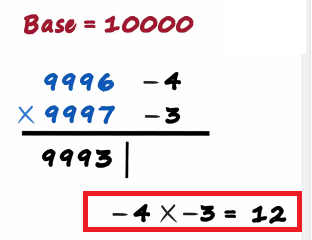
The number of zeros in the base is 4
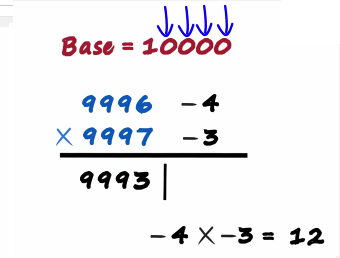
Which means we will have 4 digits on the right
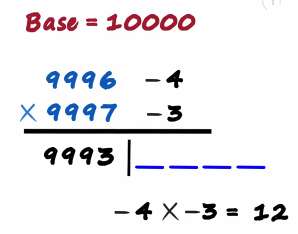
12 will be written as 0 0 1 2 that is our answer
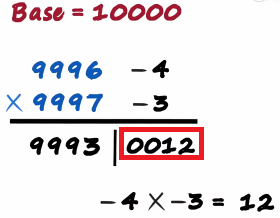
The product of 9996 times 9997 will equal 9 9 9 3 0 0 1 2
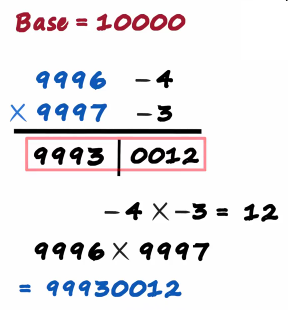
Wasn't this quick faster than a calculator .
You take notice that in all the examples we saw both numbers were below the base 98 and 97 will below 100.
9996 and 9997 well below 10,000
Don't forget the steps find the base find the deviation find the sum and find the product and we get the answer

not sure that it "easier" than the usual method
Coached mentally gets easier!
OK challenge accepted.