What Is Venn Diagrams and Set Theory?

Venn Diagrams is a visual representation of sets and of course of the set theory. But this post is about the practical uses Venn diagrams and set theory have in other fields of mathematics and how it shows the relationship of mathematical notation and graphical representation. But a disclaimer this will be a three or four part post!

Set theory is the study of a collection of objects formally called sets. This might sound boring but it is one of the most important studies of mathematics because it has a practical application in almost all fields of mathematics. I used a bit of set theory in my proofs of Rolles theorem, Fermat's Theorem and Mean Value Theorem.

Basic set theory notation

In set theory you typically describe the relationship of different types of sets. A set can consist of numbers, objects like fruit or even probabilities! You might want to describe things like objects that a set have in common or are they in the same subset etc. The notation is fairly easy to understand. The following is some of the notation:

You can represent a set with an alphabetical letter like A, B, C....
Think of this letter as a bag that contains objects.

So here is how you declare a set:

Let A be a set of numbers or cars etc.

We would usually describe the set of objects characteristics by saying it is an element of a certain type of thing or other set even! It is almost like describing the type of species or nationality of the set. We would usually write “element of” by writing a E. so here is how one describe a set of numbers:

Let A be a set of numbers such that A E of Real numbers.

This basically this means that the set A has Real numbers as objects.

OK, this is a basic way to declare and describe a set. Now I will show you assign object values in the set.

We do this by using “=” which means equal to and we just put in the objects between these curly braces “{ }”. So here is how one would use it.

Set A = {1,2,2.5,5,6,7,8}

This would mean that A only consists of these numbers inside the curly bracket!
But there are ways to declare an infinite set. You can show this by saying something like this:

A = {Real}

This would mean that all the real numbers is in the set A.

You can also exclude numbers or other subsets from the set that you are describing by using a backslash .
Here is how you would remove all integers from a set of real numbers.

A = {real \ integers}

You can also remove a single number or objects like this:

A = {Real \ 1}

You could also describe a set by using square brackets [ ] and rounded brackets ( ). This represents a set of numbers. Now there is only two numbers in these brackets a start point and an end point. So here is a visual representation of a number line to show you this:

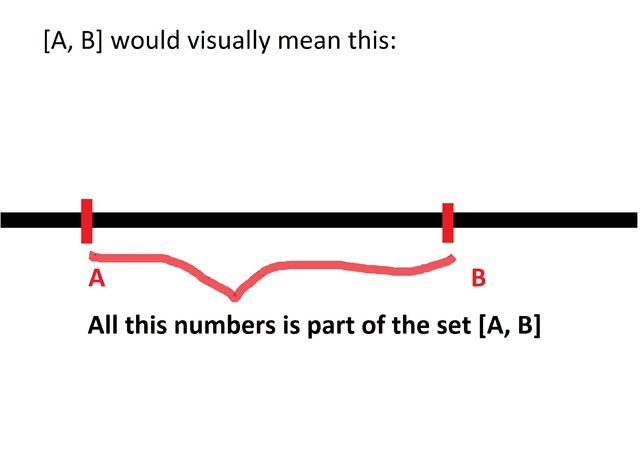
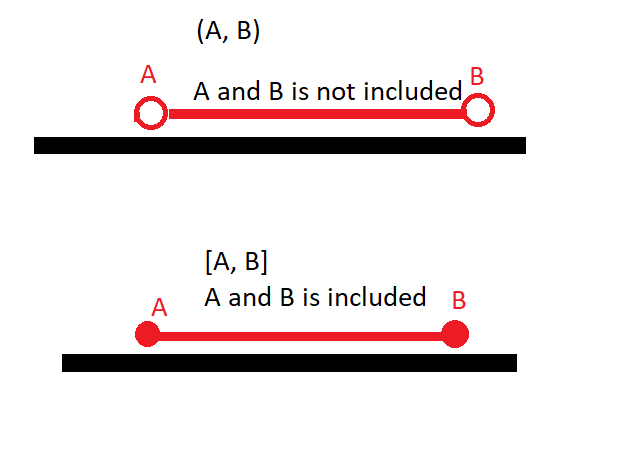
The only difference between the brackets is that the square brackets would mean that the numbers A,B in [A, B] is included in the set and with the rounded “Open Braces” (A, B) would mean that the numbers A and B is excluded in the set.

Now we can add objects in a set like this:

Let A E integers
A = [1, 3]
This would mean that A = {1,2,3}

Or could define it like this

Let A E integers
A = (1, 3)
This would mean that A = {2}

Now know how can we define a set and in our next post we will show how to express the relationship between sets in Set theory!
I Hope you all enjoyed reading this post and now that you know a bit of set theory and why it is used for leave a comment down below on your thoughts! All images used in this post was made by me!

As always thanks for reading!

what do you think? leave a comment down below. Do not forget to upvote, Resteem and follow my blog spot!
check out more posts Here

Image Credit: My own Creation